16g!:16p|p61:!g61<>#5 88+> :0\\2p^ # >g6v 5\r\n3D KH QD 6C 6S AD AS 8H 2H QS >06g1+06pv^ 3 >$$ 16g55+*36p046p156p066p076p>36g06gg05p3v5v6< 0\r\n6S 8D 4C 8S 6C QH TC 6D 7D 9D vg71g70 _v#-g40g60`96g+96v>07g17g`96 g+:96p.@ >*56p05g66g` |>05g2g!#^_05g76g`|\r\n3C QS 2S 4H JH 3D 2D TD 8S 9H > ^ >^ ^ <\r\n5H QS 8S 6D 3C 8C JD AS 7H 7D\r\n. . .\r\n. . .\r\n. . .\r\n. . .", "Yep, I *hate* this problem. \r\nNot only is there an enormous amount of input data that makes our program huge in size.\r\nBut it contains a lot of different cases, rules and logic that needs be represented in our program\r\n\r\nBut none the less I tried to come up with an compact algorithm for scoring a set of cards\r\n\r\n~~~\r\nGet(@\"https://projecteuler.net/project/resources/p054_poker.txt\")\r\n .Where(p => GetScore(p.deck_1) > GetScore(p.deck_2))\r\n .Count()\r\n .Dump();\r\n~~~\r\n\r\n~~~\r\nint GetScore(Card[] cards) {\r\n List SUMS = new List{ H*H*H*H*H, C*C*C*C*C, S*S*S*S*S, D*D*D*D*D };\r\n\r\n int[] array = new int[15];\r\n int score = 0;\r\n int flushSum = 1;\r\n int highCard = 0;\r\n int highGroup = 0;\r\n int straightIndex = 0;\r\n\r\n foreach(Card c in cards) {\r\n highCard = Math.Max(highCard, c.value);\r\n flushSum *= c.suit;\r\n if (array[c.value] > 0)\r\n highGroup = Math.Max(highGroup, c.value);\r\n array[c.value]++;\r\n }\r\n\r\n for(int i = 1; i < 15; i++)\r\n {\r\n score += (array[i]-1)*(array[i])*256;\r\n \r\n if (array[i] > 0 && array[i-1] > 0)\r\n straightIndex++;\r\n }\r\n score += highCard;\r\n score += highGroup * 15;\r\n\r\n if (straightIndex == 4)\r\n score += 2540;\r\n if (SUMS.Contains(flushSum))\r\n score += 2550;\r\n \r\n return score;\r\n}\r\n~~~\r\n\r\nThe different values are carefully crafted in such a way, that you can compare the score of two hands and get the winner\r\n\r\n Card | Calculation | Score\r\n---------------------|----------------|---------------------------------------------\r\nHigh Card | {0-14} * [1] | = {0-14}\r\nHigh Card (in Group) | {0-14} * [15] | = {0-210}\r\nOne Pair | 2 * [256] | = 512 *(+ HighCard)* *(+ HighGroup)*\r\nTwo Pairs | 4 * [256] | = 1024 *(+ HighCard)* *(+ HighGroup)*\r\nThree of a Kind | 6 * [256] | = 1536 *(+ HighCard)* *(+ HighGroup)*\r\nStraight | [2540] | = 2540 *(+ HighCard)* *(+ HighGroup)*\r\nFlush | [2550] | = 2550 *(+ HighCard)* *(+ HighGroup)*\r\nFull House | 10 * [256] | = 2560 *(+ HighCard)* *(+ HighGroup)*\r\nFour of a Kind | 12 * [256] | = 3072 *(+ HighCard)* *(+ HighGroup)*\r\nStraight Flush | [2540] + [2550]| = 5090 *(+ HighCard)* *(+ HighGroup)*\r\nRoyal Flush | [2540] + [2550]| = 5090 *(+ HighCard)* *(+ HighGroup)*\r\n\r\nOne last side note: A **royal flush** is not really a independent rank. Because of the \"highest card in the rank\" rule a royal flush is always better than a straight flush (because the highest card is an ace)\r\n", 1, 5949695, 2543, 118, 1009, 376);
+ Do(55, "Lychrel numbers", "If we take 47, reverse and add, `47 + 74 = 121`, which is palindromic.\r\n\r\nNot all numbers produce palindromes so quickly. For example,\r\n\r\n~~~\r\n349 + 943 = 1292,\r\n1292 + 2921 = 4213\r\n4213 + 3124 = 7337\r\n~~~\r\n\r\nThat is, 349 took three iterations to arrive at a palindrome.\r\n\r\nAlthough no one has proved it yet, it is thought that some numbers, like `196`, never produce a palindrome. A number that never forms a palindrome through the reverse and add process is called a Lychrel number. Due to the theoretical nature of these numbers, and for the purpose of this problem, we shall assume that a number is Lychrel until proven otherwise. In addition you are given that for every number below ten-thousand, it will either (i) become a palindrome in less than fifty iterations, or, (ii) no one, with all the computing power that exists, has managed so far to map it to a palindrome. In fact, `10677` is the first number to be shown to require over fifty iterations before producing a palindrome: `4668731596684224866951378664` (53 iterations, 28-digits).\r\n\r\nSurprisingly, there are palindromic numbers that are themselves Lychrel numbers; the first example is `4994`.\r\n\r\nHow many Lychrel numbers are there below ten-thousand?\r\n\r\n> NOTE: Wording was modified slightly on 24 April 2007 to emphasise the theoretical nature of Lychrel numbers.\r\n", "v v-1\\+g02<\r\n0 v/+55\\+g01\\p01%+< $ v/+55\\+g01\\p01%+<\r\n>\"}P\"*>::0\\>:!#v_\\55+*\\:55 ^>:!#v_\\::0\\>:!#v_\\55+*\\:55 ^\r\n >$ .@ >$+38* #v ^# < |-p02:$<\r\n ^_^#!:-1 <\\+1\\$$<^$$<", "Not much to say about this one. I reuse the isPalindrome code from P-36 and bruteforce through all the numbers. \r\nI think it would be really useful to cache the intermediate results - but our befunge space is too small for such data structures :/", 0, 10470329, 2215, 56, 5, 249);
+ Do(56, "Powerful digit sum", "A googol (`10^100`) is a massive number: one followed by one-hundred zeros; `100^100` is almost unimaginably large: one followed by two-hundred zeros. Despite their size, the sum of the digits in each number is only 1.\r\n\r\nConsidering natural numbers of the form, ab, where `a, b < 100`, what is the maximum digital sum?", "vXXX ######################################################################\r\n XXX ######################################################################\r\n ######################################################################\r\n\r\n> \"c\"v _v# `*95:<\r\nv+\"I~\"<\\\"c\":< >:55+%|\r\n>1-:0\\:\"F\"%v >1-:|:-1 <\r\n|:p/\"F\"\\+5 <@.g1$#2$<\r\n>$188*2p020p10p>030p\"~J\"+>1-:::\"F\"%5+\\\"F\"/g10g*20g+:55+/v\r\n >21p > 1-:|^$< |:p/\"F\"\\+5%\"F\":\\p03+g03:%+55p02<\r\n ^g03_^#`g1># ^#2g03$<", "Here we iterate through the values of a (1..99) and do (manually) the long multiplication. \r\nBecause we have to implement the multiplication manually we get every result from a^1 to a^99 an can easily get the digitsum for these.\r\nThen we remember the maximum digitsum and vòila, problem solved.\r\n\r\nA few optimizations:\r\n - We ignore values where `a%10 == 0`, because these result in numbers consisting mostly of zeroes, and those will never have a high digitsum\r\n - We also ignore values for a<45, because the numbers are just to short to be really significant.", 0, 62461749, 13915, 75, 11, 972);
+ Do(57, "Square root convergents", "It is possible to show that the square root of two can be expressed as an infinite continued fraction.\r\n\r\n~~~\r\nsqrt(2) = 1 + 1/(2 + 1/(2 + 1/(2 + ... ))) = 1.414213...\r\n~~~\r\n\r\nBy expanding this for the first four iterations, we get:\r\n\r\n~~~\r\n1 + 1/2 = 3 /2 = 1.5\r\n1 + 1/(2 + 1/2) = 7 /5 = 1.4\r\n1 + 1/(2 + 1/(2 + 1/2)) = 17/12 = 1.41666...\r\n1 + 1/(2 + 1/(2 + 1/(2 + 1/2))) = 41/29 = 1.41379...\r\n~~~\r\n\r\nThe next three expansions are `99/70`, `239/169`, and `577/408`, but the eighth expansion, `1393/985`, is the first example where the number of digits in the numerator exceeds the number of digits in the denominator.\r\n\r\nIn the first one-thousand expansions, how many fractions contain a numerator with more digits than denominator?\r\n", "v\r\n\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n ###############################################################################\r\n\r\n>77*8*2+>:0\\:\"O\"%1+\\\"O\"/2+p:0\\:\"O\"%1+\\\"O\"/8+p:0\\:\"O\"%1+\\\"O\"/72*+p:0\\: v\r\n |+1:-1p+*84/\"O\"\\+1%\"O\":\\0:p++*298/\"O\"\\+1%\"O\":\\0:p+*45/\"O\"\\+1%\"O\"<\r\n >$ 1\"O\"6p1\"O\"62*p1\"O\"56*p v\r\nv <\r\n>60*70p61*80p62*90p60*71p61*81p v > 0>$ v\r\nv*\"o\"9 p040p121p111p19*26 < ^p11_^#`g11 :-g02*5\"O\"<\r\n> 010p\"O\"5*>1-:::20p:\"O\"%1+\\\"O\"/70g2++g\\:\"O\"%1+\\\"O\"/80g2++g2*10g++:55+%:#^_v\r\n ^ _v#:p01/+55p++2g09/\"O\"\\+1%\"O\":g02<\r\n v p09%+99+6g09p08%+99+6g08p07%+99+6g07$< > 0>$ v\r\n ^p12_^#`g12 :-g02*5\"O\"<\r\n >010p\"O\"5*>1-:::20p:\"O\"%1+\\\"O\"/71g54*++g\\:\"O\"%1+\\\"O\"/81g54*++g2*10g++:55+%:#^_v\r\n ^ _v#:p01/+55p++*45g19/\"O\"\\+1%\"O\":g02<\r\n v p19%+99+6g19p18%+99+6g18p17%+99+6g17$<\r\n >11g21g`!#v_40g1+40pv\r\n|: -1< <\r\n>$40g.@", "I was a bit lazy with this problem. The first thing i did was search on OEIS for the numerator and denominator sequences.\r\nAnd I found both, they are **A123335** and **A000129**.\r\nBut still there are two mayor problems:\r\n - First these are recursive functions, so we need to store the last and the second last result. This is again the reason why our programs exceeds the Befunge-93 size restrictions. We need three fields for the numerator and three for the denominator (Current value | Last value | Second last value).\r\n - Second the numbers become big. Like *really* big. The last values get close to four hundred digits. So - again - we need to do the calculations manually *(long multiplication and addition)*\r\n\r\nIn the end we have a reasonable fast program with six 79*5 arrays for value storage.", 0, 87464066, 15023, 80, 54, 153);
+ Do(58, "Spiral primes", "Starting with 1 and spiralling anticlockwise in the following way, a square spiral with side length 7 is formed.\r\n\r\n~~~\r\n37 36 35 34 33 32 31\r\n38 17 16 15 14 13 30\r\n39 18 05 04 03 12 29\r\n40 19 06 01 02 11 28\r\n41 20 07 08 09 10 27\r\n42 21 22 23 24 25 26\r\n43 44 45 46 47 48 49\r\n~~~\r\n\r\nIt is interesting to note that the odd squares lie along the bottom right diagonal, but what is more interesting is that 8 out of the 13 numbers lying along both diagonals are prime; that is, a ratio of `8/13 = 62%`.\r\n\r\nIf one complete new layer is wrapped around the spiral above, a square spiral with side length 9 will be formed. If this process is continued, what is the side length of the square spiral for which the ratio of primes along both diagonals first falls below `10%`?", "v####\r\nv##\r\nv#\r\nv### > > > >$0v \r\n > > $1v \r\n >::2\\`#^_:2-!#^_:2%!#^_:9\\`#^_:3%!#^_:5%!#^_1 :v\r\n2>^:11p1-0\\>:2% !#v_v v ++!!+1-g< # ^ < >v\r\n3 3 ^\\+1\\/2< \\ >3-#v_$$ 1>12g\\ !|>|\r\np 31 vp01p03p04 g11p12< >:*11v1 >$1 #$^\r\n1 p+ >120pv v%g04*10g^ >\\:::*11 g%1-!\\^>^\r\n3 3g >$1\\> :#v_ $ 21g >:#^_$1-!! ^\r\np 03 >:!#^_\\1+\\2v\\ ^_^#!%2/\\g03p< v p33+1g33 <\r\n> ^1 ^p02*2g02/ <>:*40g%20g2/:20^\r\n ^_^#%4g32+g31_v#`\\*+55g33p32:+1g32< < \r\n @.+3*2/4-2g32$<", "It\'s obvious that the bottleneck of this program is the primality test.\r\nThe numbers become here too big to create a sieve and \"normal\" prime testing takes too long.\r\nSo we use the [Miller-Rabin primality test](http://en.wikipedia.org/wiki/Miller-Rabin_primality_test) that I implemented a while ago (thank [mathblog.dk](http://http://www.mathblog.dk)). \r\nThe rest is just enumerating all the diagonals until `primes*1020g3*10gg\"0\"-55+*20 v \r\n v\"d\"\\+8%\"d\":g03+-\"0\"gg01+1*3g< \r\n >/p30g1+30p20g1+:93+-#v_$10g1v \r\n|-2+!-1g02!-\"u\" g01p02<0p01+ < \r\n \r\n v1p12051p > 061p > 51g61g 11p^>11g21g+!#v_11g2%21g2%+2%31^ \r\n |- **88 2p15:< > 31p0^ >51g\"m\"+61gp v \r\nv\"+~h\"< | -**882 p16:+1g16< \r\n+ >51g1+^ \r\n* v < \r\n>13p>13g:1-13p#v_ v\r\nv+\"a\"%+*298:g31< > >^ 5\r\n>12p892*+/:892*+%\"a\"+22p892*+/\"a\"+32pv $ $ 5\r\nv p430 < $ $ 6\r\n>014p 55*6*8* >:3%1+24p::\"d\"%8+\\\"d\"/g\"m\"+24g2gg :\" \"\\`#^_:\"~\"`| 8\r\n ^-1 _v#-\" \"_v#-9p41+1:g41< *\r\n >$$ ^ *\r\nv < >$ ^ *\r\n > $ ^ 1\r\n>:3%1+24p::\"d\"%8+\\\"d\"/g\"m\"+24g2gg :\" \"\\`#^_:\"~\"`| 5\r\n^-1_v#: _v#-\"e\"< p\r\n ^ : p43+1g43< 0\r\n >$34g23g`#v_ ^ 2\r\n >34g23p 32g22g12g 43p53p63p ^ 5\r\n p\r\nv <\r\nv p51-1< \r\n>15g:\"d\"%8+\\\"d\"/g\"m\"+15g3%4+3gg:25g+25p15g:\"d\"%8+\\\"d\"/p15g:| \r\n >$25g.@\r\n", "This task had a lot of Befunge specific problems, but first let\'s look at the solving strategy:\r\n - We go through all `26^3` passwords and test look if they generate illegal characters (smaller 32 or bigger 127).\r\n - We also see if one of the first twelve characters is a space, assuming the first word is no longer than twelve characters.\r\n - The leaves us with around one-hundred viable passwords.\r\n - We use the fact that in the English language the letter `e` is pretty common and take the password with the highest count of `e`.\r\n - The rest is just decrypting the text and counting the values.\r\n\r\nNow to our Befunge specific problems: \r\n - First we need to input the raw data. Our best call is inserting the data directly into the program and then parsing it in the first step into an array.\r\n - The next problem is the missing xor operator. To perform an xor operation we need to go through all bits and xor them individually (`a xor b == (a+b) % 2`). This is an extremely pricey operation. And to speed this up we generate an complete 128x128 xor look up-table with all possible xor operations.\r\n\r\nAll in all a not really optimal problem for Befunge but still a fun challenge", 1, 37085853, 6302, 273, 128, 107359);
+ Do(60, "Prime pair sets", "The primes `3`, `7`, `109`, and `673`, are quite remarkable. By taking any two primes and concatenating them in any order the result will always be prime. For example, taking `7` and `109`, both `7109` and `1097` are prime. The sum of these four primes, `792`, represents the lowest sum for a set of four primes with this property.\r\n\r\nFind the lowest sum for a set of five primes for which any two primes concatenate to produce another prime.", "vXXXX /#...## ####\r\n XXX # # ####\r\n XXXXXX. . ####\r\n XX . . ####\r\n XXX . . ####\r\n XXXXX # # ####\r\n XXX ##...## ####\r\n\r\n>55+12p \"d!\"*22p 26522g+++62p 22g:*52p 12g22g*42p 523p v \r\n v p232< >032p v \r\nv p0+1g26p0g26:\" \"< _^#`g23g24<\r\n>\"X\"32g:12g%62g+\\12g/p32g>32g+:42g\\` #v_$>32g1+:32p:12g%62g+\\12g/g\" \"-| \r\n ^p/g21\\+g26%g21:\\\" \":< ^ <\r\nv <\r\n >52g >1-:0\\:22g%9+\\22g/1+pv \r\n |: <\r\n v $<\r\n>22g1+ >1- :0\\8\\p v\r\n |: <\r\nv $<\r\n >22g >1-:0\\9+0p v\r\n |: <\r\n v $<\r\n>0 113p > ::12g%62g+\\12g/g\"X\"-#v_:13g8+0p:713gp22g13g1+:13p\\`#v_v \r\n |-g24:+1 < <\r\nv $< <\r\n>114p 024p \"@@@@` \"+****34p 015p 025p 035p 045p 055p 065p v \r\nv < < \r\n>14g#v_34g.@\r\n >14g1+5g1+:14g1+5p22g-#v_14g1-14p24g714g1+5g1+g-24p^ \r\n vg41g32g+1g5+1g417g42g43<\r\n >-*+`#v_14g1-14p24g714g1+5g1+g-24p ^ \r\n v-1g41<\r\n :>:1+5g1+14g1+5g9+\\g#v_$ ^ \r\n >|:-1 <\r\n $\r\n >14g1+5gv > > > >$0v \r\n v < >55+*\\:v > > $1v\r\n >:1+8\\g#v_:::1\\1+8\\p36p9+0g26p1+v>:9+0g:26 g>\\:#v_$+:2\\`#^_:2-!#^_:2%!#^_:9\\`#^_:3%!#^_:5%!#^_1 :v\r\n v2:< ^\\/+55< v\\ p13:+1g13:_v#-3 2g-|< >:11p1-0\\>:2% !#v_v v ++!!+1-g< # ^ < >v\r\n v < $<- ^\\+1\\/2< \\ >3-#v_$$ 1>31g\\ !|> |\r\n g vp01p03p04 g11p12< >:*11v1 >$1 #$^ :\r\n 2 >120pv v%g04*10g^ >\\:::*11 g%1-!\\^>^\r\n : >$1\\> :#v_ $ 21g >:#^_$1-!! ^\r\n + >:!#^_\\1+\\2v\\ ^_^#!%2/\\g03p<\r\n 1 ^p02*2g02/ <>:*40g%20g2/:20^\r\n v g62\\g62g0+9: <\r\n ^ p+1g63+9\\<<\r\n > > > >$0v \r\n >55+*\\:v > > $1v\r\n > \\>\\:#v_$+:2\\`#^_:2-!#^_:2%!#^_:9\\`#^_:3%!#^_:5%!#^_1 :v\r\n ^\\/+55< v\\ p13:+1g13:_v#-3 :11p1-0\\>:2% !#v_v v ++!!+1-g< # ^ < >:1^\r\n ^\\+1\\/2< \\ >3-#v_$$ 1>31g\\ !|>|\r\n vp01p03p04 g11p12< >:*11v1 >$1 #$^>:0^\r\n >120pv v%g04*10g^ >\\:::*11 g%1-!\\^>^\r\n >$1\\> :#v_ $ 21g >:#^_$1-!! ^\r\n >:!#^_\\1+\\2v\\ ^_^#!%2/\\g03p<\r\n ^p02*2g02/ <>:*40g%20g2/:20^\r\n >24g714g1+5g1+g+24p14g1+14p14g5g14g1+5p v \r\n >14g23g-| >24g714g1+5g1+g+34p v\r\n >34g24g714g1+5g1+g+`#^_ >14g1-14p24g7 v \r\n^ # 6 # 10p 288** 20p>20g1-20p10g>1-:0\\2*20g88*/+^^ $<0p03+1g03 p+*2g02/*88g<\r\n ##### 0 >20g1-20p030p0>1+::::*\\-2/20g1+*+:\"}\"8*\\`#^_:\"ec\"*`#^_30g88*%9+30^\r\n >g>1-:0\\5\\p:0\\6\\p:0\\7\\p:#v_$ 01-60p011p v\r\nv< $_^#!: <0 < < <$$<\r\n>611gg1+611gp611gg12p511gg13p12g10g-!#v_13g\"_ \"+`#v_712gg#^_13g88* %9+13g88*/12v\r\n^/611g1-g2*+g\"d\"%14g\"d\"/-*#^_10g1-11g`!|\r\n^2*+g:.+55+,21g1+:21p10g-#v_\" = \",,,,.@ >88*/60g2*+g\"d\"/-#^_v\r\n^gg126/*88gg125+9%*88gg125<0p120 <", "Pretty cool problem, I have to say.\r\n\r\nIt\'s one of these problem that you can easily make dynamic. In the middle-left of this program you see the number `6` surrounded with `#`.\r\nThis is the \"amount of resulting numbers\" parameter of our program. For this Euler-problem you need to set this to `6`.\r\nBut for debugging purposes I mostly tested it with `3`. And if you want you can try it out with bigger numbers `7` or `8`.\r\n*(But then you need to move the code down a bit - otherwise the cache-part will intersect with the code-part)*.\r\n\r\nWith this number we first generate all the [polygon-numbers](https://en.wikipedia.org/wiki/Polygonal_number) from `3` to `SIDES_COUNT + 2` with the formula `(n-2) * (n^2 - n)/2 + n`.\r\nThen we go recursively through all these numbers. First we test triangle[1] with square[1], then with square[2] and so on. *(The recursion is - as always - just a stack and a stack pointer)*.\r\n\r\nA last note: This was *(until now)* probably the hardest program to fit in the befunge 80x25 size restriction.\r\nI *barely* managed to get it (and now its exactly 80x25) and I had to use quite some trickery.", 0, 50105245, 14414, 80, 25, 28684);
+ Do(62, "Cubic permutations", "The cube, `41063625 (345^3)`, can be permuted to produce two other cubes: `56623104 (384^3)` and `66430125 (405^3)`. \r\nIn fact, `41063625` is the smallest cube which has exactly three permutations of its digits which are also cube.\r\n\r\nFind the smallest cube for which exactly five permutations of its digits are cube.", "v $ # ... #\r\n $ # #\r\n $ . .\r\n . .\r\n $ . .\r\n $ . .\r\n # #\r\n # ... #\r\n v _v#!:p/g42\\+ <\r\n>3 28p \"K\": 24p 88+: 25p*:26p >1-:0\\:24g%4^\r\nv < v+1 <\r\n0 |-g02<\r\n>1+:::**:22p 0\\v v\\-1 <>20p0>:3*:24g%4+\\24 g/g:|\r\n$ v+55:<>\\1>9*\\:|: @$$.g/g42\\+4%g42:+1$ <\r\n >%\\:#^|#/+55\\$<+ > 3*:2+:24g%4+\\24g/g1+:28g-!|\r\n >$ #\\>#<>\\# :#+_^ >*::2v vp/g42\\+4%g42:+2\\<\r\n^p/g42\\+4%g42:+2\\1p/g42\\+4%g42:+1\\g22p/g42\\+4%g42:\\g0 <\r\n^ <", "Only after at least sixty-two mathematical programs in befunge you will **truly** appreciate a hashtable.\r\n\r\nFor real, everything would be so much better if I could retrieve this stuff in `O(1)`.\r\n\r\nMy approach is pretty straight-forward. We calculate an permutation-insensitive hash.\r\nThen store them together with the times it appeared in a hashmap *(I mean a list -.-)*.\r\nNow we just go through all the cubes until a single hash appeared five times. In C# with a Dictionary this takes around 10ms.", 1, 952323293, 363264, 505, 58, 127035954683);
+ Do(63, "Powerful digit counts", "The 5-digit number, `16807=7^5`, is also a fifth power.\r\nSimilarly, the 9-digit number, `134217728=8^9`, is a ninth power.\r\n\r\nHow many n-digit positive integers exist which are also an nth power?", "v XXXX #######################################################################\r\n XX\r\n v1\\1p12::+1 \\+g2<\r\n0 v9p03p02< \\g12:+1<^2\\p22_v\r\n1 >v v < v-\\\"P\"< :$\r\n> :v1v>0p>9>:\"0\"\\0p1+:\"O\"-|>:0g\"0\"-||!`g12<-$\r\n :p\\3v p050p04\"O\"#1 $#< :21g-|\\.\r\n 211p> 40g0g\"0\"-2 0g*50g+:55+%\"0\"v>$55+0v+@\r\n >^20|-8p04:-1g04 p05/+5 #5p0g04+<>5#$5#<^\r\n >^>30g1-:30p #^_9 ^", "After all the previous programs, this one is surprisingly ... dense (the main code-block is 54x8).\r\n\r\nThe algorithm is quickly explained for each length n we calculate the numbers `1^n`, `2^n` ... until `9^n` and see which have a length of `n`.\r\n(From `10^n` upwards the condition is impossible, because `10^n` has `(n+1)` digits).\r\n\r\nThe main problem is that the numbers exceed Int64. So we need to implement long multiplication ... again. (see problem 16, 20, 29, 56 and 57)", 0, 8880369, 2762, 80, 10, 49);
+ Do(64, "Odd period square roots", "All square roots are periodic when written as continued fractions and can be written in the form:\r\n\r\n~~~\r\nsqrt(N) = a0 + 1 / (a1 + 1 / (a2 + 1 / (a3 + ... )))\r\n~~~\r\n\r\nFor example, let us consider `sqrt(23)`:\r\n\r\n~~~\r\nsqrt(23) \r\n = 4 + sqrt(23) - 4 \r\n = 4 + 1 / ( 1 / ( sqrt(23) - 4 ) ) \r\n = 4 + 1 / ( 1 + ( sqrt(23) - 3 ) / 7)\r\n~~~\r\n\r\nIf we continue we would get the following expansion:\r\n~~~\r\nsqrt(23) = 4 + 1/(1 + 1/(3 + 1/(1 + 1/(8 + ... ))))\r\n~~~\r\n\r\nThe process can be summarised as follows:\r\n\r\na | Step 1 | Step 1 |Step 1 \r\n-----|------------------------|-------------------------|----------------------\r\n`a0` | `4`, `1/(sqrt(23) - 4` | `1*(sqrt(23) + 4) / 7` | `1 + (sqrt(23) - 3)/7`\r\n`a1` | `1`, `7/(sqrt(23) - 3` | `7*(sqrt(23) + 3) / 14` | `3 + (sqrt(23) - 3)/2`\r\n`a2` | `3`, `2/(sqrt(23) - 3` | `2*(sqrt(23) + 3) / 14` | `1 + (sqrt(23) - 4)/7`\r\n`a3` | `1`, `7/(sqrt(23) - 4` | `7*(sqrt(23) + 4) / 7` | `8 + (sqrt(23) - 4)/1`\r\n`a4` | `8`, `1/(sqrt(23) - 4` | `1*(sqrt(23) + 4) / 7` | `1 + (sqrt(23) - 3)/7`\r\n`a5` | `1`, `7/(sqrt(23) - 3` | `7*(sqrt(23) + 3) / 14` | `3 + (sqrt(23) - 3)/2`\r\n`a6` | `3`, `2/(sqrt(23) - 3` | `2*(sqrt(23) + 3) / 14` | `1 + (sqrt(23) - 4)/7`\r\n`a7` | `1`, `7/(sqrt(23) - 4` | `7*(sqrt(23) + 4) / 7` | `8 + (sqrt(23) - 4)/1`\r\n\r\nIt can be seen that the sequence is repeating. For conciseness, we use the notation `sqrt(23) = [4;(1,3,1,8)]`, to indicate that the block `(1,3,1,8)` repeats indefinitely.\r\n\r\nThe first ten continued fraction representations of (irrational) square roots are:\r\n\r\n~~~\r\nsqrt( 2) = [1;(2)], period=1\r\nsqrt( 3) = [1;(1,2)], period=2\r\nsqrt( 5) = [2;(4)], period=1\r\nsqrt( 6) = [2;(2,4)], period=2\r\nsqrt( 7) = [2;(1,1,1,4)], period=4\r\nsqrt( 8) = [2;(1,4)], period=2\r\nsqrt(10) = [3;(6)], period=1\r\nsqrt(11) = [3;(3,6)], period=2\r\nsqrt(12) = [3;(2,6)], period=2\r\nsqrt(13) = [3;(1,1,1,1,6)], period=5\r\n~~~\r\n\r\nExactly four continued fractions, for `N <= 13`, have an odd period.\r\n\r\nHow many continued fractions for `N <= 10000` have an odd period?", "v###\r\n #####\r\n0\r\n\">>1-:0\\951p11p021p131v v12g14 p150 p13/g<\r\nI vp01g03_v#-g01:_v#- <>g+31g/ :31g*21g-21v1\r\ni @ >:30p:20 g\\/+2/: 30g^^12p14:<>11g21g:*-3 ^\r\n * . > #$ >$30g::*11g-||+g15-1g13p<\r\n\"+ $ ^p02:p010g11p1< v\\+1\\<>>0>\\#+ #1:#$_v\r\n>^^_^#-2: < _^# %2$<", "For this I had to re-use my old [integer-squareroot](https://en.wikipedia.org/wiki/Integer_square_root) implementation \r\nand I ported an [algorithm](http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/cfINTRO.html#section7) for calculating the continued fraction to befunge.\r\n\r\nThe rest is just iterating through all the values and trying to optimize for speed.\r\n\r\nHere two useful snippets I made while solving this puzzle:\r\n\r\n - Calculating the **sum** of an zero-terminated array on the stack: `>\\# :#+_+`\r\n - Calculating the **count** of an zero-terminated array on the stack: `0>\\#+ #1:#$_$`", 0, 24936143, 5804, 51, 9, 1322);
+ Do(65, "Convergents of e", "The infinite continued fraction can be written, `sqrt(2) = [1;(2)]`, `(2)` indicates that `2` repeats ad infinitum.\r\nIn a similar way, `sqrt(23) = [4;(1,3,1,8)]`.\r\n\r\nIt turns out that the sequence of partial values of continued fractions for square roots provide the best rational approximations.\r\nLet us consider the convergents for `sqrt(2)`.\r\n\r\n~~~\r\n1 + 1/2 = 3/2\r\n1 + 1/(2+ 1/2) = 7/5\r\n1 + 1/(2+ 1/(2+ 1/2)) = 17/12\r\n1 + 1/(2+ 1/(2+ 1/(2+ 1/2))) = 41/29\r\n~~~\r\n\r\nHence the sequence of the first ten convergents for `sqrt(2)` are:\r\n~~~\r\n1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, ...\r\n~~~\r\n\r\nWhat is most surprising is that the important mathematical constant,\r\n\r\n~~~\r\ne = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...]\r\n~~~\r\n\r\nThe first ten terms in the sequence of convergents for `e` are:\r\n~~~\r\n2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, ...\r\n~~~\r\n\r\nThe sum of digits in the numerator of the 10th convergent is `1+4+5+7=17`.\r\n\r\nFind the sum of digits in the numerator of the 100th convergent of the continued fraction for `e`.", "v $$$ #######################################################################\r\n\r\n #######################################################################\r\n\r\n v -1<\r\n>\"F\">:9+\"0\"\\0p:9+\"0\"\\2p:|\r\nv\"c\"p040p2\"O1\"p0\"O0\" $<\r\n >$1 v@.:1-3%:!| >:1+3/2*v +>g*+40g+:55+%\"0\"+30g2p55+/40p:9-|\r\n>:| >2-#^_1 >20 p \"O\"v # $\r\n| ># #+ #1 #: #- #12# ^# ># ^# <\r\n$ >\\v >\\:!|\r\n>0\"F\">:9+2g\"0\"-:| >:!|1 +<\r\n ^ -1_ ^#1<", "Nice algorithm if you see the pattern in the numerators and denominators.\r\n\r\n~~~\r\ndenom(n+1) = denom(n) + numer(n) * frac(n)\r\nnumer(n+1) = denom(n)\r\n~~~\r\n\r\nand the fraction at position n is calculated by ([OEIS-A003417](https://oeis.org/A003417)):\r\n\r\n~~~\r\nint GetFrac(int idx)\r\n{\r\n if (idx == 0) return 2;\r\n if ((idx-1) % 3 == 0) return 1;\r\n if ((idx-1) % 3 == 1) return ((idx+1)/3)*2;\r\n if ((idx-1) % 3 == 2) return 1;\r\n return 2;\r\n}\r\n~~~\r\n\r\nThe rest is just multiplication and long addition (we exceed the 64bit range) a hundred times ...", 0, 477489, 124, 80, 14, 272);
+ Do(66, "Diophantine equation", "Consider quadratic Diophantine equations of the form:\r\n\r\n~~~\r\nx^2 – Dy^2 = 1\r\n~~~\r\n\r\nFor example, when `D=13`, the minimal solution in `x` is `649^2 – 13×180^2 = 1`.\r\n\r\nIt can be assumed that there are no solutions in positive integers when D is square.\r\n\r\nBy finding minimal solutions in `x` for `D = {2, 3, 5, 6, 7}`, we obtain the following:\r\n\r\n~~~\r\n3^2 – 2×2^2 = 1\r\n2^2 – 3×1^2 = 1\r\n9^2 – 5×4^2 = 1\r\n5^2 – 6×2^2 = 1\r\n8^2 – 7×3^2 = 1\r\n~~~\r\n\r\nHence, by considering minimal solutions in `x` for `D <= 7`, the largest `x` is obtained when `D=5`.\r\n\r\nFind the value of `D <= 1000` in minimal solutions of `x` for which the largest value of `x` is obtained.", "vYYY ################\r\n XBXX ################\r\n ZZZ ################\r\n N\r\n OOO ################\r\n ################\r\n ################\r\n ################ v 9::p4+9\\g5+9::p1+9\\g2+9: <\r\n ################ >+6g\\9+5p:1-\\!v0 <\r\n ################ v $_::9+1g\\9+0p:^\r\n v _v#-*\"}\"8p13:+1g13$< # <\r\n>\"@ \":*:**21p331p013p88 +>:8+0\\8v >11g.@ >+8p:1-\\!| >-22g/22p35*^\r\nv p02:p010g13<$<_^#!:-1p< ^9\\g2+9::<# ^*:g21g13p21-g21*g 22<\r\nvp01g03_v#-g01:_v#- <^ :30p:20 g\\/+2/: 30g^ >88 +>:8+0\\5p:8+0\\4p:8+^ > `^ >$$ $v2\r\n > >$30g:41p:*31g-| >$164*1p164*4p012p122pv 0 >$1+:9-8- !| 03\r\n^p02:p010g13p13+1g13 # 3# 5# *# # ^\r\n>:::9+0g\\9+1g32g*+13g+:v v 53< |!\\-1:g42$< >::9+7g\\9+9g- |\r\n|\\-1:p2+9\\%g12 p31/g12 < # >$ 014p35 *>:9+0\\ v|!-9g43-1p7g43%g12p41/g12 :+g<\r\n>$35*:::9+4g\\9+5g32g*+13g+v $ >*>2 4p35* >::24g+# 6-34p9+2g24g9+2gv>1v7\r\n>:::9+4g\\9+5g32g*+13g+v <|!\\-1:g42$< |\\-1:p7< ^ # < -g\r\n|\\-1:p6+9\\%g12p31/g12:<> # :9+0\\v| !-9 g43-1p9g43%g12p41/g12:+g9g43$114p35* ^ >*>2 4p35*#9> ::2 4g+6-34p9+6g24g9+6g31g**14g+^> 4g +3^\r\n ^ _^#\\-1:p< ^53$< ^ $<", "Okay I admit this one took me five days to complete (with two days pause in between, because of I kinda got frustrated).\r\n\r\nI needed eight numbers that were too big for int64 so I encoded them in base-67108864 (`2^26`).\r\nThe reason for this specific number (and I had to fail first to see the problem with bigger bases) is that the biggest calculation I do is `D_0 * D_0 * D * 1`.\r\nWhich is maximally `2^26 * 2^26 * 2^10` which fits *barely* in an signed 64-bit integer.\r\n\r\nAlso I needed to first write code to multiply two numbers, both in base-67108864 and both bigger than `2^63`. Let me tell you that was no fun and long-addition is far easier to implement than long-multiplication.\r\nEspecially after first I did everything wrong and then had to redo it :/\r\n\r\nThe first running version of this program was full of debug statements (even more than normally) and had a size of 200x60. (You can look at it, it\'s the `Problem-066 (annotated)` file).\r\nBut after that I managed to shrink it quite a bit :D I even *(barely)* managed to fit it in the 80x25 restriction.\r\nI have the feeling I\'ve gotten pretty good at compacting my programs...\r\n\r\nBut back to the interesting stuff, how did I solve this one:\r\n\r\nI can\' really explain everything in detail here, so I give you a few useful links:\r\n\r\n - [https://en.wikipedia.org/wiki/Diophantine_equation](https://en.wikipedia.org/wiki/Diophantine_equation)\r\n - [https://en.wikipedia.org/wiki/Pell\'s_equation](https://en.wikipedia.org/wiki/Pell%27s_equation)\r\n - [https://en.wikipedia.org/wiki/Generalized_continued_fraction](https://en.wikipedia.org/wiki/Generalized_continued_fraction)\r\n - [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/cfINTRO.html#section9.4](http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/cfINTRO.html#section9.4)\r\n\r\nIf you want to have the `(x|y)` solution for a number D:\r\n\r\n - First you calculate the continuous fraction of `sqrt(D)`\r\n - For the continuous fraction you calculate the convergents `hi / ki` (read the link about Pell\'s equation)\r\n - Now you just test if `hi` and `ki` are solutions, if not go on to the next convergent pair\r\n\r\nIn the end the algorithm is really not that complex (around 30 lines in C#) but all the numbers get so big - and you need to multiply and add the already big numbers together so you get even bigger immediate values.\r\nSo on a last note I could say ... I wished the numbers in befunge were unlimited.", 0, 262481767, 55831, 80, 25, 661);
+ Do(67, "Maximum path sum II", "By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.\r\n\r\n~~~\r\n3\r\n7 4\r\n2 4 6\r\n8 5 9 3\r\n~~~\r\n\r\nThat is, 3 + 7 + 4 + 9 = 23.\r\n\r\nFind the maximum total from top to bottom in [triangle.txt](https://projecteuler.net/project/resources/p067_triangle.txt) (right click and \'Save Link/Target As...\'), a 15K text file containing a triangle with one-hundred rows.\r\n\r\n*NOTE: This is a much more difficult version of [Problem 18]. It is not possible to try every route to solve this problem, as there are 299 altogether! If you could check one trillion (1012) routes every second it would take over twenty billion years to check them all. There is an efficient algorithm to solve it. ;o)*", "$$>\"d\" 00p00g1-20p010p>10g3*:20g1+g\"0\"-55+*\\1+20g1+g\"0\"-+10g20g1+p10g1+:10p20g-1-#v_20g:1-20p010p#v_v\r\n59 ^ < < v\r\n73 41 v <\r\n52 40 09 > $v\r\n26 53 06 34 >00g2-:10p 20p > 10g20g1+g 10g20g2+g : 10g1+20g2+g -:0`>#^_-> + 10g20g1+ p 10g:1-10p#v_20g:1-:20p10p#v_ 01g.@\r\n10 51 87 86 81 ^ < <\r\n61 95 66 57 25 68\r\n90 81 80 38 92 67 73\r\n30 28 51 76 81 18 75 44\r\n84 14 95 87 62 81 17 78 58\r\n\r\n... ... ...", "see [Problem-018]", 1, 650537, 266, 299, 101, 7273);
+ Do(68, "Magic 5-gon ring", "Consider the following \"magic\" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.\r\n\r\n\r\n\r\nWorking clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely.\r\nFor example, the above solution can be described by the set: `4,3,2; 6,2,1; 5,1,3`.\r\n\r\nIt is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.\r\n\r\nTotal | Solution Set\r\n------|------------------------\r\n9 | `4,2,3; 5,3,1; 6,1,2`\r\n9 | `4,3,2; 6,2,1; 5,1,3`\r\n10 | `2,3,5; 4,5,1; 6,1,3`\r\n10 | `2,5,3; 6,3,1; 4,1,5`\r\n11 | `1,4,6; 3,6,2; 5,2,4`\r\n11 | `1,6,4; 5,4,2; 3,2,6`\r\n12 | `1,5,6; 2,6,4; 3,4,5`\r\n12 | `1,6,5; 3,5,4; 2,4,6`\r\n\r\nBy concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is `432621513`.\r\n\r\nUsing the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings.\r\nWhat is the maximum 16-digit string for a \"magic\" 5-gon ring?\r\n\r\n", "v X X ##########\r\n X OOOOOOOOOO\r\n>\":\"v v < <\r\nv < vp1+9-\"0\"g0+9p03:-1g03\"O\" <\r\n>90p030p>30g9+0g1-:30g9+0p\"0\"-:70p0\\`|\r\nv g03_^#! -\"O\"g1+9g07 #<$\r\n>:#v_70g5` >|\r\nv-1< v _v#!`g039$ <\r\n>:#v_ 70g9-! ^\r\nv-1< >\"X\"70g9+1p\":\"30g1+:30p9+0p^\r\n>:#v_ 90+0g91+0g92+0g++51p70g9-! ^\r\nv-1< >91+0g\"/\"- 98+0g\"/\"- 99+0g\"/\"- v\r\n>:#v_90g\"0\"-70g` ^\r\nv-1< v-\"/\"g0+79 -\"/\"g0+69 -\"/\"g0+89 <\r\n>:#v_ 92+0g93+0g94+0g++51g-!!70g9-!+ ^\r\nv-1< >96+0g\"/\"- 94+0g\"/\"- 95+0g\"/\"- v\r\n>:#v_90g\"0\"-70g` ^\r\nv-1< v-\"/\"g0+39 -\"/\"g0+29 -\"/\"g0+49 <\r\n>:#v_ 94+0g95+0g96+0g++51g-!!70g9-!+ ^\r\nv-1< >92+0g\"/\"- 91+0g\"/\"- 90+0g\"/\"- v\r\n>:#v_90g\"0\"-70g` ^\r\nv-1< @ ... ... ... ... ...<\r\n>:#v_96+0g97+0g98+0g++51g-!!70g9-!+ ^\r\nv89<\r\n>+0g99+0g91+0g++51g-!!90g\"0\"-70g`!!+ ^", "The solution to this problem is similar to problem-043.\r\nWe iterate through all possible 10-digit combinations but abort most paths pretty early through a few rules.\r\nThis leads to a pretty quick execution time an a not so big program.\r\n\r\nI even managed to squeeze all in only half the available width so the other half has space enough for an ASCII representation of the magic 5-gon ring :D.\r\n*(You can see the result in the `problem-068 (visual)` file)*\r\n\r\nThe main piece (excluding the act of pressing everything in such a small space) was formulating the rules.\r\nThe more (an the earlier triggering) rules, the less paths we have to traverse and the faster our program gets:\r\n*(I needed to index the elements of the ring, so I went clockwise from the outermost to the inner elements.*\r\n\r\nThe rules are:\r\n - `N_3 > N_0`, `N_5 > N_0`, `N_7 > N_0`, `N_9 > N_0`. We want `N_0` to be the smallest element to avoid getting the same solution multiple times, only rotated. (Also it is stated that we start counting from the smallest outer element)\r\n - `N_0 <= 5`, otherwise it can\'t be the smallest outer element\r\n - `N_1 <> 9`, `N_2 <> 9`, `N_4 <> 9`, `N_6 <> 9`, `N_8 <> 9`, otherwise we won\'t get an 16-digit number\r\n - `N_2+N_3+N_4 = N_0+N_1+N_2`, `N_4+N_5+N_6 = N_0+N_1+N_2`, `N_6+N_7+N_8 = N_0+N_1+N_2`, `N_8+N_9+N_1 = N_0+N_1+N_2`. Our condition for the ring to be \"magic\"", 0, 304112, 78, 39, 25, 6531031914842725);
+ Do(69, "Totient maximum", "Euler\'s Totient function, `phi(n)` (sometimes called the phi function), \r\nis used to determine the number of numbers less than n which are relatively prime to n. \r\nFor example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, `phi(9)=6`.\r\n\r\nn | Relatively Prime | phi(n) | n/phi(n)\r\n---|------------------|--------|-------\r\n2 | 1 | 1 | 2\r\n3 | 1,2 | 2 | 1.5\r\n4 | 1,3 | 2 | 2\r\n5 | 1,2,3,4 | 4 | 1.25\r\n6 | 1,5 | 2 | 3\r\n7 | 1,2,3,4,5,6 | 6 | 1.1666...\r\n8 | 1,3,5,7 | 4 | 2 \r\n9 | 1,2,4,5,7,8 | 6 | 1.5\r\n10 | 1,3,7,9 | 4 | 2.5\r\n\r\nIt can be seen that n=6 produces a maximum `n/phi(n)` for `n <= 10`.\r\n\r\nFind the value of `n <= 1,000,000` for which `n/phi(n)` is a maximum.", "v000000 // Project Euler - Problem 69\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\nv >p50g1+50pv @.g07<\r\nv ^1g0< >30g1+:30p40g- #v_\"}}@\"**60p 0>:1g70g*v$\r\n>170p\"P\":10p3:20p*40p230pv^5g03_^#-\" \"g+1/g01\\%g01:g03g` |\r\n>\"X\"30g:10g%\\10g/1+p30g>30g+:40g\\` #v_$>30g1+:30p:10g%\\10g/1+g\" \"-|^ p07<\r\n ^p+1/g01\\%g01:\\\" \":< ^ <", "I had a really complicated solution where I tried to generate an Phi Sieve and had to work around a lot of corner cases.\r\nThen I looked at [this](http://www.mathblog.dk/project-euler-69-find-the-value-of-n-%E2%89%A4-1000000-for-which-n%CF%86n-is-a-maximum/) solution and - well - it\'s faster and simpler than mine.\r\nSo I translated it to befunge.", 0, 35542, 16, 80, 10, 510510);
+ Do(70, "Totient permutation", "Euler\'s Totient function, `phi(n)` [sometimes called the phi function], \r\nis used to determine the number of positive numbers less than or equal to n which are relatively prime to n. \r\nFor example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, `phi(9)=6`.\r\n\r\nThe number 1 is considered to be relatively prime to every positive number, so `phi(1)=1`.\r\n\r\nInterestingly, `phi(87109)=79180`, and it can be seen that `87109` is a permutation of `79180`.\r\n\r\nFind the value of `n`, `1 < n < 10^7`, for which `phi(n)` is a permutation of n and the ratio `n/phi(n)` produces a minimum.", "v00000 000 // Project Euler - Problem 70\r\n ccc\r\n ?? ?? ??\r\n# ... #\r\n. . . .\r\n. . .\r\n. . . .\r\n# ... #\r\n \r\n>55*6*:10p57*:20p*40p230p\"2(\"*11p\"}(\"*21p022p112p\"}22 \"***31p1v>030p v>g 0\\v v\\-1 < >g 0\\v v\\-1 <\r\nvp08*8**::**::8p31p30:\" \" _^#`g03g04< 2 v+55:<>\\1>9*\\:| 2 v+55:<>\\1>9*\\:|\r\n>\"X\"30g:10g%\\10g/3+p30g>30g+:40g\\` #v_$>30g1+:30p:10g%\\10g/3+g\" \"-| 7 >%\\:#^|#/+55\\$< 8 >%\\:#^|#/+55\\$< \r\n ^p+3/g01\\%g01:\\\" \":< ^ < >$ #\\>#<>\\# :#+_+^>$ #\\>#<>\\# :#+_vv\r\nvg11 <^ < v -+<-\r\n>:42p::10g%\\10g/3+g\"X\"-#v_:1+>:52p::10g%\\10g/3+g\"X\"-#v_42g52g*:72p31g`#v_72g22g*42g1-52g1-*:82p12g*`#v_^v_v\r\n >$12g.@ v $< < v < <\r\n^_^#-g12:+1 < <^_^#-g12:+1 < 020p040p121p141p\"}}@\"**60pv\r\nv0 < >01+*v\r\n>1+ :3*7%!#v_:61p:3*7/:71p7*61g3*-:0`| >81p61g7*91p41g91g*21g81g*`#v_v\r\n|-g06: < <>01-*^v p04g16p02g17p12g19p14g18<\r\n>$20g.\"/ \",,55+,40g.@ ^ < <", "For every denominator from `1` to `1 000 000` we generate a possible fraction where the numerator is `(d * 3) / 7`.\r\n(Every other fraction is either greater than `3/7` or has a greater difference than the generated).\r\n\r\nNow everything thats left is finding the fraction with the smallest difference to `3/7`.\r\n\r\nThe difference of two fractions is calculated (without floating points) by:\r\n\r\n~~~\r\nn1/d1 - n2/d2 == (n1*d2 - n2*d1)/(d1*d2)\r\n~~~\r\n\r\nThe rest is just iterating through all the possible fractions and in each step remembering the current best.\r\n\r\nWe don\'t even need to reduce the result to get a *proper* fraction. \r\nIf it could be reduced we would have got the reduced version first.\r\n(Because it has an smaller denominator).", 0, 77428679, 11981, 73, 8, 428570);
+ Do(72, "Counting fractions", "Consider the fraction, `n/d`, where `n` and `d` are positive integers.\r\nIf `n699**:10p3777***:20p*40p230p\" \":03p13p\"}}@\"**11p192*+21p022pv >030p0>::10g%\\10g/3+g\"X\"-#v_v\r\nvp+3/g01\\%g01:\\\"#\":-1 :| ^ <>\\10g/3+pv\r\nv $<0 _^#`g03g04<|-g04:+1 < <\r\n>\"X\"30g:10g%\\10g/3+p30g>30g+:40g\\` #v_$>30g1+:30p:10g%\\10g/3+g\" \"-|$\r\n > v ^p+3/g01\\%g01:\\\" \":< ^ <\r\nv_^#!:p1+9\\\" \":-1$091pv v p23*g23-1p24*<\r\nv < 42g11g`#v_32g12g42g1--+12p>21g1-22g`22g9+1g:10g%\\10g/3+g42g*11g`!*|>9+1g:10g%\\10g/3+g*11g`!*|\r\n > ^vg01:g1+9g22p24/g+3/g01\\%g01:g1+9g22g24<^g22g24`g1+9g22g05%\\10g/3+g22g0`22g9+1g22g8+1g-!*!-32g\\/32p22g9+1g1+22g9+1p^g\r\n >*!-32g\\/32p22g9+1g1+22g9+1p #@ #. #g #2 #1 #< ^9\r\n ^!-g1+8g22g1+9g22`0g22p24/\\g24:g+3/g01\\%g01:g1+9g22_^#!`p22:-1g220p1+<", "First we need the number of proper reduced fractions for a denominator `d`.\r\nThis is the amount of numbers `d limit`. Because every other factor will only increase `x`.\r\n - The value of phi is always calculated from the last phi value. So we don\'t need to totally recalculate it in every step.\r\n\r\nAfter looking a little bit around this is not ***the** fastest solution to this problem.\r\nBut it\'s the one I found and I think it\'s reasonable fast.", 1, 339636085, 50606, 486, 1047, 303963552391);
+ Do(73, "Counting fractions in a range", "Consider the fraction, `n/d`, where n and d are positive integers. If `n\"}`\"*11p051p0v\r\nvp12*\"(2\" < v+1 < <\r\n>1+:1+2/61p:71p:3/1+>:61g\\`!#v_:21g%71g3+g!|>81g11g`91g11g`+#^_081g21gv\r\n|-g11: >#$ #< ^p19+g19g17p18+g18:p+3g19%<\r\n>$51g.@ ^p19g17p18:p15+1g15<", "Here we brute-force through every possible denominator `d` (from 1 to 12000).\r\nFor every denominator the valid numerators are between `floor(d/3)` and `ceil(d/2)`.\r\n\r\nThe only problem is that we don\'t know if a fraction is proper.\r\nTo solve this we use a `12000x12000` array where we mark the already found fractions and every multiple of them.\r\nWhen we now find a new one we can test if we have already found the fraction (in a reduced form).\r\n\r\nBut a `12000x12000` array is *quite* big, the resulting b93-file was 140MB big.\r\nBut we know that most of the array will never be accessed,\r\nonly the columns between `d/3` and `d/2` are important and the biggest range is in the last row (`LIMIT/3 - LIMIT/2`).\r\nSo in each array-acess we modulo the x coordinate by `LIMIT/3 - LIMIT/2` (= `2000`).\r\nNow our array has only a size of `12000x2000` and the befunge-file is *only* 23MB big.\r\n\r\nThe program is not that fast, but that\'s mostly because of it\'s raw size, the algorithm is quite good (`200ms` when I implement it in C#)", 1, 1281174401, 202458, 2000, 12010, 7295372);
+ Do(74, "Digit factorial chains", "The number 145 is well known for the property that the sum of the factorial of its digits is equal to 145:\r\n\r\n~~~\r\n1! + 4! + 5! = 1 + 24 + 120 = 145\r\n~~~\r\n\r\nPerhaps less well known is 169, in that it produces the longest chain of numbers that link back to 169;\r\nit turns out that there are only three such loops that exist:\r\n\r\n~~~\r\n169 -> 363601 -> 1454 -> 169\r\n871 -> 45361 -> 871\r\n872 -> 45362 -> 872\r\n~~~\r\n\r\nIt is not difficult to prove that EVERY starting number will eventually get stuck in a loop. For example,\r\n\r\n~~~\r\n69 -> 363600 -> 1454 -> 169 -> 363601 (-> 1454)\r\n78 -> 45360 -> 871 -> 45361 (-> 871)\r\n540 -> 145 (-> 145)\r\n~~~\r\n\r\nStarting with 69 produces a chain of five non-repeating terms,\r\nbut the longest non-repeating chain with a starting number below one million is sixty terms.\r\n\r\nHow many chains, with a starting number below one million, contain exactly sixty non-repeating terms?", "v X ########## // Project Euler - Problem 74\r\n CCC\r\n XXXX |------------------------------------------------------------|\r\n\r\n# ... #\r\n. . . .\r\n. . .\r\n. . . .\r\n# ... #\r\n\r\n>98+8*9*11p\"+&\"*2/21p\"}}@\"**31p042p31g>1-:0\\:11g%v\r\nvg11:-8*:+\"W~\"2p+4/g11\\%g11:/3*\"\'C\"2p<|:p+4/g11\\ < v <\r\n%>8-:11g%\\11g/4+p3\",!\"*2+:11g%\\11g/4+^$ >:70g:1+70p9 +0v\r\n\\^**\"CCQ\"3p+4/g11\\%g11:+\"+~\"3p+4/g11\\<>070p11|-+55g07*g07 p<^ p22+g22_v\r\n>11g/4+p2\"m\"8*:11g%\\11g/4+ v ^%g11:00< # >:55+%9+0v>11g/4+g: ^$\r\nv1$p+4/g11\\%g11:-7*:+\"W~\"2p<>12g22g1+:22p9+2p32g1+32p12g0\\:|:/+55\\g <^\\%g11:g21<\r\n>:12p022p092p032p32g9+2g12g-|-g21g2+9g23 <>$>\\# :#+_+:12p31g`!| \r\n v < <^ <<\r\n+>22g\"<\"-#v_42g1+42p>1>:9+2g31g`#v_::22g1+\\-\\9+2v\r\n1 >$42g.@ > ^ ^+1_v#-g23: \"}\"8* 20p \"}}`\"** 30p 30g>:0\\:20g%\\20v\r\nv p060$_^#!\\-1:p+3/g<\r\n v p08+1g08<\r\n>180p>80g::*4*\\6*2++30g`#v_>80g1+:90p>::2**\\80g2**+30g` |\r\n @.g06< ^p09:+1g09<\r\nv g13g12p16++p14:+*:g08*:g09p13:**2g09g08p12:-*:g08*:g09<\r\n>`#v_ >1>:61g*30g`#v_:21g7*31g+5*41g+# *81p:61g*:20g%\\20g/3+g:#v_v\r\n >21g31g21p31p^ ^+1 <># $# ^# _v#<`\\0_v#-g18:< \r\n ^p06-1g06p+3/g02\\%g02:\\-10*g16: :50g\\-3v\r\n>\"d\"30p1>:30g`#v_:50p060p1>:50g-!#^_::::50g\\-`#^_: 3v\r\n >1+:1+g.@ ^+1p+3g05+3\\p06:+g06g+3-\\g05\\+<", "The big trick is - similar to many other problems - *caching*.\r\n\r\nThis problem remembered me a little bit of problem-15.\r\nWe use a `100x100` grid to remember pre-calculated sums.\r\n\r\nSo in cell [3, 6] is the amount of sums which result in `6`, start with `3` and have all summands in descending order:\r\n\r\n~~~\r\n3 + 3\r\n3 + 2 + 1\r\n3 + 1 + 1\r\n~~~\r\n\r\nYou see `cache[3,6] = 3`.\r\n\r\nNow to find a new value (for example `[4, 7]`) we just have to look at the our cache:\r\n\r\n~~~\r\n7 = 4 + x\r\nsum(x) = 7-4 = 3\r\n\r\n// first_digit_of_x <= first_digit, because of the descending order\r\nsum(x) = sum([n, 3]); n = [1..3]\r\nsum(x) = [3, 3] + [2, 3] + [1, 3] \r\n~~~\r\n\r\nYou see it\'s important not only to remember the amount but also the first (= highest) summand, \r\nso we can guarantee the oder of the sums (an this way that we don\'t count any sums multiple times).\r\n\r\n*Note:* `cache[a, a]` is always `1`. But the problem rules dictate that when we calculate the final result we must ignore this (`100 = 100` is not a valid solution)\r\n\r\nOh and this algorithm improves the native approach (enumerating all solutions) from `O(wtf)` to `O(n^2)`.\r\nI\'m not sure if I would be still alive when my first algorithm finishes :)\r\n\r\n----\r\n\r\n**Edit:** \r\n\r\nI did a little optimization:\r\n\r\nThe value of cell `[d, s]` is now the sum of all previous cells from `[0, s]` to `[d, s]`.\r\n\r\nThis way we don\'t have to iterate through all the cells from 0 to d every time.\r\nWe can just look at the biggest cell which contains the sum of all previous.", 1, 296178, 32, 104, 108, 190569291);
+ Do(77, "Prime summations", "It is possible to write ten as the sum of primes in exactly five different ways:\r\n\r\n~~~\r\n7 + 3\r\n5 + 5\r\n5 + 3 + 2\r\n3 + 3 + 2 + 2\r\n2 + 2 + 2 + 2 + 2\r\n~~~\r\n\r\nWhat is the first value which can be written as the sum of primes in over five thousand different ways?", "v00000 00 // Project Euler - Problem 77\r\n XXXXXX\r\n# ... #\r\n\r\n# ... #\r\n. . . .\r\n. . .\r\n. . . .\r\n# ... #\r\n\r\n> \"e\" :10p 1 :20p*40p230p\" \":02p12pvv03:+1g03< >030p 0>::10g%\\10g/2+g\"X\"-#v_:30g:1+30p:v\r\nv <># p# :# v# _^#`g03g04<|-g04:+1 \"X\"30g:10g%\\10g/2+p30g>30g+:40g\\` #v_$^>10g%\\10g/2+g\" \"-|>$30g:50p10g*>1-:0\\:10g%\\10g/4+pv\r\n ^p+2/g01\\%g01:\\\" \":< ^ < ^_v#: <\r\nvp08\"d\"p07*\"}(\"$ <\r\n0 >061p31g>:0\\`#v_:4+51g\\g61g+61pv\r\n>1+:11p021p031p>31g:50g-\\2g:41p11g`!*!#v_11g41g-:51p| ^-1 <\r\n^ _v#!`g07g12< >111g31g4+pv >$21g61g:1v\r\n ^ ># 1# 1# g# .# @# p13+1g13$.@ \r\n v+1p+1/g01\\+1%g01:g04_^#:%g02g05$$ <\r\n>\"}}@\"**20p\"~|\"+10p111p1>:40p050p0>:60p::2/1+:*3*\\:2/1+\\2%2*1-*+2/:40g`#^_4 v\r\n ^+1p05-\\g05*-1*2%2/2g06g+1/g01\\+1%g01:-\\g0<", "Again the algorithm is from [MathBlog](http://www.mathblog.dk/project-euler-78-coin-piles/).\r\nI can\'t really say that I understand the algorithm fully (and the MathBlog guy says he neither).\r\n\r\nBut for the best explanation you better read his article.", 1, 1191633332, 170946, 251, 256, 55374);
+ Do(79, "Passcode derivation", "A common security method used for online banking is to ask the user for three random characters from a passcode.\r\nFor example, if the passcode was 531278, they may ask for the 2nd, 3rd, and 5th characters;\r\nthe expected reply would be: 317.\r\n\r\nThe text file, keylog.txt, contains fifty successful login attempts.\r\n\r\n~~~\r\n319 680 180 690 129 620 762 689 762 318\r\n368 710 720 710 629 168 160 689 716 731\r\n736 729 316 729 729 710 769 290 719 680\r\n318 389 162 289 162 718 729 319 790 680\r\n890 362 319 760 316 729 380 319 728 716\r\n~~~\r\n\r\nGiven that the three characters are always asked for in order,\r\nanalyse the file so as to determine the shortest possible secret passcode of unknown length.", "v\r\n ++++++++++ 319 680 180 690 129 620 762 689 762 318\r\n ++++++++++ 368 710 720 710 629 168 160 689 716 731\r\n ++++++++++ 736 729 316 729 729 710 769 290 719 680\r\n ++++++++++ 318 389 162 289 162 718 729 319 790 680\r\n ++++++++++ 890 362 319 760 316 729 380 319 728 716\r\n ++++++++++\r\n ++++++++++ ##########\r\n ++++++++++\r\n ++++++++++ XXXXXXXXXX\r\n ++++++++++\r\n\r\n>55+>:1\\:v>:55+/1+30p:55+%4*66++20p020g0+30gg\"0\"-:50p66v\r\n |:-1p< v1g070p+1g07+1g062p+1g07+1g052p+1g06+1g052< +\r\n >$ 77*^>+50g1+p070g1+60g1vv< < p +\r\n |\\-1:p+1g05+1g060p+<1|!\\-1: # $# 0# 9# 0# p# 9#<>:66++7g#^_ :90g:1+9^ + p\r\n >:90g-!#v_:::66++9g1+\\65++9g1+g*!#^_::v + 0\r\n ^p9++66\\ g02:-1p9++66\\g9++56p02g9++66:< 6 2\r\n >$0>:66++9g. v >020g2+30gg\"0\"-:70p6^ 0\r\n @$_^#!-g09:+1< ^p7++66p06:-\"0\"gg03+1g<", "This is one of the problems i really enjoyed solving.\r\n\r\nWe make the assumption that our final pass code has no duplicate digits (If we hadn\'t found a solution we would need to change that part).\r\nThis is a pretty good assumption because no attempt has a duplicate digit in it.\r\n\r\n> *Side note:* This leaves us with a 8-digit code, because only 8 digits are used (`4` and `5` are missing).\r\n\r\nFirst we generate a 10x10 grid where we remember the absolute ordering of the numbers from our attempts (eg `3` is before `8` or `9` is after `2`).\r\nIf we inspect this data we can see that every field (for numbers in our pass code) is set, the fifty login attempts generate more than enough data for this.\r\n\r\n> *Side note:* In fact there are only 33 **unique** login attempts\r\n\r\nThen we can simply sort an array of the valid digits with this ordering. And - frankly - I find this is a really neat way of doing this.\r\n\r\nBecause we sort only eight numbers, sorting-performance is not a big factor.\r\nSo I searched for the simplest (easiest to implement) sorting algorithm I could find.\r\nThis was surprisingly not Bubble-sort, but [Gnome Sort](https://en.wikipedia.org/wiki/Gnome_sort) (accordingly to the author \"the simplest sort algorithm\").\r\nWhich was pretty easy to implement in Befunge (and for 8 values is the runtime of O(n^2) not *that* bad).\r\n\r\nA last thing: For a problem where I used an two-dimensional cache **and** that has input data I was surprised to fit everything in the Befunge-93 80x25 size restrictions.\r\n", 0, 12040, 0, 56, 21, 73162890);
+ Do(80, "Square root digital expansion", "It is well known that if the square root of a natural number is not an integer, then it is irrational. \r\nThe decimal expansion of such square roots is infinite without any repeating pattern at all.\r\n\r\nThe square root of two is `1.41421356237309504880...`, \r\nand the digital sum of the first one hundred decimal digits is `475`.\r\n\r\nFor the first one hundred natural numbers, \r\nfind the total of the digital sums of the first one hundred decimal digits for all the irrational square roots.", "v X X XX X\r\n ############################################################\r\n\r\n @ ############################################################\r\n .\r\n g ############################################################\r\n 0\r\n ^9$># #< v v < v <\r\n $ v_^#-\"d\"\\+1:< <>$\"<\">1-::9+5g\\9+1p:#^_$0>:::9+3g55+%55+*v\r\n>090p2>:20p\"d\">::*20g-#v_$^|!:-1p5+8\\-g07g06p04 # <\\\r\n # v\"<\":$_^# !:-1< >::9+1g40g-60p:9+3g20g45***70p0>70g60g`!|5\r\n ^ <>1-:0\\9+1p:0\\v ^ \";\"p04* :g02p5\"D\"0p<#+ 65\r\n |:p5+9\\0:p3+9< >9+1g-!#v_::9+5g\\9+1g`!#v_$20g1-20^ 1 0+\r\n >$\"D\"1p\"d\"020p>20g:*40p \"<\">1-::9+3g20g 45***40gv ^p06+\"d\"g<+\r\n ^ _> #v^#-\"<\":+1< |:p5+9\\%\"d\"p 04/\"d\":+#<# ^# < > \";\"-|\r\n ^ !:-1p020p09+g09g02p3\"D\"+g02*+55%+55g3\"D\"$<", "A short look to [Wikipedia](https://en.wikipedia.org/wiki/Methods_of_computing_square_roots#Digit-by-digit_calculation) finds us a neat algorithm to calculate the square-root digit-by-digit.\r\n\r\nI have optimized it a little bit with the target to use not so many variables:\r\n\r\n~~~\r\nIEnumerable DRoot(int r)\r\n{\r\n BigInteger c = r;\r\n BigInteger p = 0;\r\n int x = 0;\r\n\r\n for (ii = 0; ii < 100; ii++)\r\n { \r\n for (x = 0;(x+1)*(20*p + (x+1)) <= c;x++);\r\n c = 100*c - 2000*p*x - 100*x*x;\r\n p = p*10 + x;\r\n }\r\n \r\n return p;\r\n}\r\n~~~\r\n\r\nThe algorithm is pretty simple, but *god* do I hate long addition/multiplication in Befunge.\r\n\r\nWe need 120 base-10 digits for the numbers `p`and `c`.\r\nIn our program we use base-100 notation. This way we can fit the numbers in a single befunge-93 row \r\n**and** can simply multiply by 100 with a single left shift operation.", 0, 540417723, 116439, 69, 18, 40886);
+ Do(81, "Path sum: two ways", "In the 5 by 5 matrix below, the minimal path sum from the top left to the bottom right, \r\nby only moving to the right and down, is indicated in bold red and is equal to 2427.\r\n\r\n~~~\r\n131 673 234 103 018\r\n201 096 342 965 150\r\n630 803 746 422 111\r\n537 699 497 121 956\r\n805 732 524 037 331\r\n~~~\r\n\r\nFind the minimal path sum, in matrix.txt (right click and \"Save Link/Target As...\"), \r\na 31K text file containing a 80 by 80 matrix, \r\nfrom the top left to the bottom right by only moving right and down.", "v 4445 2697 5115 ... 5870\r\n 1096 0020 1318 ... 9377\r\n # ... # 9607 7385 0521 ... 9230\r\n . . . . 7206 3114 7760 ... 2187\r\n . . . 3620 8024 0577 ... 7505\r\n . . . . 1074 5438 9008 ... 6942\r\n # ... # 4295 1176 5596 ... 4757\r\n\r\n>\"d@\"*>1-:::::\"P\"%5*\"g\"+\\\"P\"/g\"0\"-\\::\"P\"%5*\"f\"+\\\"P\"/g\"0\"-\\::\"P\"%5*\"e\"+\\\"P\"/g\"0\"-\\: v\r\n |:p+\"d\"/\"P\"\\+9%\"P\":\\*:*\"~~\"p+2/\"P\"\\+9%\"P\":\\+*+55+*+55+*+55-\"0\"g/\"P\"\\+\"d\"*5%\"P\"<\r\n $ >20g8+30g\"d\"v\r\n >0>:20p 0>:30p20g9+30g2+g20g9+30g\"c\"+g20g8+30g\"d\"+g20g30g+!#v_20g!#v_30g!#v_`|\r\n |-\"P\":+1p+\"d\"g03+9g02 < < < <>20g9+30g\"c\"v\r\n |-\"P\":+1$< ^$$< ^+$< ^+$\\< ^ +g+<\r\n $\r\n >\"O\"9+\"Od\"+g.@\r\n\r\n\r\n\r\n\r\n # ... #\r\n . . . .\r\n . . .\r\n . . . .\r\n # ... #", "Well, this is practically extremely simple path finding.\r\n\r\nWe generate an array where we remember the shortest distance from [0,0] to this node.\r\nInitially we can set `distance[0, 0] = data[0,0]`\r\n\r\nThe we got through our data row by row and column by column.\r\nThe distance of every node we visit is the minimum of `top-node-distance + own value` and `left-node-distance + own value`.\r\n\r\nThen after we iterated through every single node the result is written in the bottom right corner.", 1, 1697244, 234, 500, 180, 427337);
+ Do(82, "Path sum: three ways", "NOTE: This problem is a more challenging version of Problem 81.\r\n\r\nThe minimal path sum in the 5 by 5 matrix below,\r\nby starting in any cell in the left column and finishing in any cell in the right column,\r\nand only moving up, down, and right, is indicated in red and bold; the sum is equal to `994`.\r\n\r\n~~~\r\n131 673 234 103 018\r\n201 096 342 965 150\r\n630 803 746 422 111\r\n537 699 497 121 956\r\n805 732 524 037 331\r\n~~~\r\n\r\nFind the minimal path sum, in matrix.txt (right click and \"Save Link/Target As...\"), \r\na 31K text file containing a 80 by 80 matrix, \r\nfrom the left column to the right column.", "v 4445 2697 5115 ... 5870\r\n 1096 0020 1318 ... 9377\r\n # ... # 9607 7385 0521 ... 9230\r\n . . . . 7206 3114 7760 ... 2187\r\n . . . 3620 8024 0577 ... 7505\r\n . . . . 1074 5438 9008 ... 6942\r\n # ... # 4295 1176 5596 ... 4757\r\n\r\n>\"d@\"*>1-:::::\"P\"%5*\"g\"+\\\"P\"/g\"0\"-\\::\"P\"%5*\"f\"+\\\"P\"/g\"0\"-\\::\"P\"%5*\"e\"+\\\"P\"/g\"0\"-\\: v\r\n |:p+\"d\"/\"P\"\\+9%\"P\":\\*:*\"~~\"p+2/\"P\"\\+9%\"P\":\\+*+55+*+55+*+55-\"0\"g/\"P\"\\+\"d\"*5%\"P\"<\r\n $\r\n >\"P\">1-::9\\2+gv\r\n |:p+\"d\"\\9\\< >$$v >v\r\n >$1>:20p0>:30p20g8+30g\"d\"+g40p30g>:50p40g20g9+50g2+g+::40p20g9+50g\"d\"+g`| >20g8+30g\"d\"+g40p30g>:50p40g20g9+50g2+g+::40p20g9+50g\"d\"+g`| \r\n ^ < |-\"P\":+1 p+\"d\"g05+9g02< $ |+1:-1 p+\"d\"g05+9g02< \r\n |-\"P\":+1 ># ^# $<$ <\r\n |-\"P\":+1$< >70v\r\n >$\"O\"9+\"Od\"+g70p\"O\">1-:\"X\"\\\"d\"+g:70g`!|\r\n |: $<0p<\r\n >$70g.@\r\n\r\n\r\n # ... #\r\n . . . .\r\n . . .\r\n . . . .\r\n # ... #", "As the problem description states this is similar to problem-081.\r\n\r\nAgain we generate an node-array where we remark the minimal distance from the left side to this node.\r\nInitially we can initialize the left column with its input values.\r\n(`distance[0, y] = data[0, y]`) and all the other nodes with an absurdly high number.\r\n\r\nThen we iterate through all remaining columns: \r\n\r\nFor each column `x` we go all possible ways from the previous column. That means:\r\n - Choose the start-row `y` (and do this for all possible start rows)\r\n - Get the distance to reach this row by calculating `distance[x-1, y] + data[x, y]`\r\n - Then go all the way up and down and calculate the distance on the way `distance[x-1, y] + data[x, y] + data[x, y - 1] + data[x, y - 2] ...`\r\n - For each node where this distance is lesser than the current one we update distance array.\r\n - *Optimization node:* Once we find a node where the distance is greater than a previous calculated we can stop further traversing the column (in this direction)\r\n \r\nAt the end we have an distance array where each node is the minimal distance to reach this node from the left side.\r\nOur result is then the minimal value of the most-right column.\r\n\r\n*Note:* While problem-081 hat an time complexity of O(n) this one has one of O(n^2).\r\nBut for an 80x80 array that\'s still fast enough and really not an problem.", 1, 13777233, 2106, 500, 180, 260324);
+ Do(83, "Path sum: four ways", "NOTE: This problem is a significantly more challenging version of Problem 81.\r\n\r\nIn the 5 by 5 matrix below, the minimal path sum from the top left to the bottom right, \r\nby moving left, right, up, and down, is indicated in bold red and is equal to `2297`.\r\n\r\n~~~\r\n131 673 234 103 018\r\n201 096 342 965 150\r\n630 803 746 422 111\r\n537 699 497 121 956\r\n805 732 524 037 331\r\n~~~\r\n\r\nFind the minimal path sum, in matrix.txt (right click and \"Save Link/Target As...\"), \r\na 31K text file containing a 80 by 80 matrix, \r\nfrom the left column to the right column.", "v 4445 2697 5115 ... 5870\r\n 1096 0020 1318 ... 9377\r\n # ... # 9607 7385 0521 ... 9230\r\n . . . . 7206 3114 7760 ... 2187\r\n . . . 3620 8024 0577 ... 7505\r\n . . . . 1074 5438 9008 ... 6942\r\n # ... # 4295 1176 5596 ... 4757\r\n\r\n>\"d@\"*>1-:::::\"P\"%5*\"g\"+\\\"P\"/g\"0\"-\\::\"P\"%5*\"f\"+\\\"P\"/g\"0\"-\\::\"P\"%5*\"e\"+\\\"P\"/g\"0\"-\\: v\r\n |:p+\"d\"/\"P\"\\+9%\"P\":\\*:*\"~~\"p+2/\"P\"\\+9%\"P\":\\+*+55+*+55+*+55-\"0\"g/\"P\"\\+\"d\"*5%\"P\"< >70g40g8+50g\"d\"+p v\r\n >$120p92g9\"d\"p\"Xdd\"p>0>:40p 0>:50p40g\"d\"+50g\"d\"+g\"X\"-#v_820p\"O\"40g\"d\"+50g\"d\"+p 40g0`40g8+50g\"d\"+g40g9+50g\"d\"+g40g8+50g2+g+:70p`*|\r\n |-\"P\":+1 < v ^ |-\"P\":+1$< >70g40g9+50g\"c\"+p v\r\n $ >50g0`40g9+50g\"c\"+g40g9+50g\"d\"+g40g9+50g1+g+:70p`*|\r\n |p070g07< v \"O\"9+\"Od\"+g.@ >70g40g55++50g\"d\"+pv\r\n >40g\"P\"-40g55++50g\"d\"+g40g9+50g\"d\"+g40g55++50g2+g+:70p`*|\r\n v 70g40g9+50g\"e\"+p\"X\"v\r\n >50g\"P\"-40g9+50g\"e\"+g40g9+50g\"d\"+g40g9+50g3+g+:70p`*|\r\n ^ 040p\"}}@\"**58*v v _v# -1< v<10 v 10> v < <|<\r\n v < 0 |:+<2?^#*4<2?^#$< ^<\r\n >1-:2+0\\1pv ^3< ^3< -\r\n |: < >>>v >>>v v< >>>v >>>v >>>v 2\r\nv $< 12 v 12 v #^p04<+55$<01 v 01 v 01 v >v :\r\n>40g::2+1g1+\\2+1p>#^?3>#^?3>++58*%:40p>#^?2>4*#^?2>+4*#^?2>+|>:56*-|\r\n| >4^v<>4^ #v< v<>3^ >3^ >3^\r\n>$58vv >>v >>>v ^ < < <\r\n: $ 01 v 01 v #>v >v >v >v >v >v #>v >v >v > v\r\n- >#^?2>4*#^?2>+ :|>1-:|>1 -:|>1-:|>1-:|>1-:|>1-:|>1-:|>1-:|>1-:| #\r\n1>1-::2v>3^ >3^ >55+v>56 +v>64*v>\"\'\"v>5v >0v v < v >40g3- v\r\n |:p2+ <>::1+2g2+1g\\ 2+2g 2+1 g \\` v>v # >62*v\r\n >$v ^_v#:<-1p2\\g 05+2 :-1 p 2+2\\ g2+1 :: p 05 g 2+2:_^#>40g492*+-|\r\n >0>:58* \\`| >$22 g.32 g.4 2 g.@ >40g6%1+2/2*5*5+v$ >74*v\r\n ^+1 < >#<^# ># ># ># ># ># ># #< > v\r\n^< < < < < $p04<", "This is not really a mathematical problem (or at least not with my solution).\r\n\r\nAll I did was implement the rules in my befunge program and run a randomized game for `1 000 000` turns.\r\nThis is called an [Monte Carlo algorithm](https://en.wikipedia.org/wiki/Monte_Carlo_algorithm) and if we have enough runs it becomes pretty improbable to get a wrong result.\r\n\r\nPerhaps there are some fancy mathematical solutions out there, but this works too.\r\n\r\nA note to the befunge code: It got pretty messy because of all the decisions we have to implement for the different monopoly rules,\r\nbut all we needed as storage was an 40-element array. So it wasn\'t that hard to fit it all in the 80x25 space.", 0, 146519794, 19203, 77, 20, 101524);
+ Do(85, "Counting rectangles", "By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:\r\n\r\n\r\n\r\nAlthough there exists no rectangular grid that contains exactly two million rectangles, \r\nfind the area of the grid with the nearest solution.", "vX\r\n YY YY YY\r\n>\"}}_!\"+**:10p11p051p071p>10g71g`v\r\n v*`g18g01`g14g151g-:0\\`#v_0>-:11g`#v_11p41g5v\r\n>*81g+81v>0\\^v+1g14$<#0p12*g1<\r\n^g17p14:># p#< ^", "The key to solve this problem is effectively iterating through the permutations for a given width and height (`perms[w, h]`).\r\n\r\nFirst we look at the baseline with `width=1`. The basic case `perms[1,1]` is `1`.\r\nAfter that `perms[1,h] = perms[1,h-1] + h` (so we can iterate easily through all these solutions).\r\n\r\nWith the baseline in place we can see that `perms[w, h] = perms[w, h-1] + perms[w, 1] * h`.\r\n\r\nThen we just iterate through all the possibilities and search for the smallest difference.\r\nWe can stop increasing the width when `perms[w, 1] > 2,000,000` and similar stop increasing the height when `perms[w, h] > 2,000,000` or `w > h`.\r\nThe second conditions stems from the fact that `perms[w, h] == perms[h, w]` *(it\'s a mirrored functions)*.\r\n\r\nThrough these limiting conditions and the fact that each step is pretty fast (just a few additions and multiplications) this algorithm is *really* fast.\r\n*(We only test around 10000 values before our search space is depleted)*", 0, 880151, 109, 35, 8, 2772);
+ Do(86, "Cuboid route", "A spider, **S**, sits in one corner of a cuboid room, measuring `6 by 5 by 3`, \r\nand a fly, **F**, sits in the opposite corner. \r\nBy travelling on the surfaces of the room the shortest \"straight line\" \r\ndistance from **S** to **F** is 10 and the path is shown on the diagram.\r\n\r\n\r\n\r\nHowever, there are up to three \"shortest\" path candidates for any given cuboid and \r\nthe shortest route doesn\'t always have integer length.\r\n\r\nIt can be shown that there are exactly `2060` distinct cuboids, ignoring rotations, \r\nwith integer dimensions, up to a maximum size of `M by M by M`, \r\nfor which the shortest route has integer length when `M = 100`. \r\nThis is the least value of M for which the number of solutions first exceeds two thousand; \r\nthe number of solutions when `M = 99` is `1975`.\r\n\r\nFind the least value of M such that the number of solutions first exceeds one million.", "v##### ## > >$30gv >`#v_v\r\n>\"}}@\"**50p040p0>1+:v>>1-::*70g:*+v vp01g03_^#-g01:_^#- <: g : :\r\n :+ v < >:30p:20 g\\/+2/: 30g^* 0>#1v2\r\n 71 > >#^ #p #0 2 #<$ v 7gv+:88*%\"9\"`#^_:88+%:9`#v_:2-#v_v 2 :082g8\r\n p2 > > > > # >$>$0>|80/0 \r\n 0p |!-8_^#-7:_^#-6:_^#-5:_^# -3:< g +p7^<\r\n 80 > ^< 0 <^:p010 <^<-! ^10#<\r\n > ^ >^ >:55+%:7-!#^_:3-!#^_2-!#^_:3%2-#^_^>^ $g -\r\n@._^#`g05p04:+g04g08$_^#!: < <>\\^", "The spider essentially travels on the hypotenuse of a triangle with the sides `A` and `B+C`.\r\nFor it to be the shortest path the condition `A <= B+C` must be true.\r\n\r\nThe amount of integer-cuboids for a given value M is \"All integer-cuboids with `A=M`\" plus integer-cuboids(M-1).\r\nIn our loop we start with `M=1` and increment it in every step.\r\nWe also remember the last value (for `M-1`) and loop until the value exceeds one million.\r\n\r\nFor a given value `A = M` we go through all possible `BC` value (`0 <= BC <= 2*A`) and test if `M^2 + BC^2` is an integer-square.\r\nIf such a number is found and `BC <= A` then this means we have found `BC/2` additional cuboids (there are `BC/2` different `B+C = BC` combinations where `B <= C`)\r\nIf, on the other hand `BC > A` then we have only found `A - (BC + 1)/2 + 1` additional cuboids (because the condition`A <= BC` must be satisfied).\r\n\r\nOne of the more interesting parts was the `isSquareNumber()` function, which test if a number `x` has an integer square-root.\r\nTo speed this function up *(it takes most of the runtime)* we can eliminate around 12% of the numbers with a few clever tricks.\r\nFor example if the last digit of `x` is `2`, x is never a perfect square-number. Or equally if the last hex-digit is `7`.\r\nIn our program we test twelve conditions like that:\r\n\r\n~~~\r\nx % 16 > 9\r\nx % 64 > 57\r\nx % 16 == 2\r\nx % 16 == 3\r\nx % 16 == 5\r\nx % 16 == 6\r\nx % 16 == 7\r\nx % 16 == 8\r\nx % 10 == 2\r\nx % 10 == 3\r\nx % 10 == 7\r\nx % 3 == 2\r\n~~~\r\n**Sources:**\r\n - [ask-math.com](http://www.ask-math.com/properties-of-square-numbers.html)\r\n - [johndcook.com](http://www.johndcook.com/blog/2008/11/17/fast-way-to-test-whether-a-number-is-a-square/)\r\n - [stackoverflow.com](http://stackoverflow.com/questions/295579/fastest-way-to-determine-if-an-integers-square-root-is-an-integer)\r\n\r\nIf none of this pre-conditions is true we have to manually test the number.\r\nWe use the same the same [integer-squareroot](https://en.wikipedia.org/wiki/Integer_square_root) algorithm as in previous problems.\r\nIf `isqrt(x)^2 == x` the we can be sure that x is a perfect square number.", 0, 599659030, 91822, 66, 10, 1818);
+ Do(87, "Prime power triples", "The smallest number expressible as the sum of a prime square, prime cube, and prime fourth power is 28. \r\nIn fact, there are exactly four numbers below fifty that can be expressed in such a way:\r\n\r\n~~~\r\n28 = 2^2 + 2^3 + 2^4\r\n33 = 3^2 + 2^3 + 2^4\r\n49 = 5^2 + 2^3 + 2^4\r\n47 = 2^2 + 3^3 + 2^4\r\n~~~\r\n\r\nHow many numbers below fifty million can be expressed as the sum of a prime square, \r\nprime cube, and prime fourth power?", "v000000000 \r\n################################################################\r\n# ... #\r\n. . . .\r\n. . .\r\n. . . .\r\n# ... #\r\n\r\n>150p0>:50g::+50p\\1pv\r\n |-\">\":+1 <\r\nv $<\r\n>\"}\"8* : 8 : 2v>\"X\"\\:10g%\\10g/2+p:40 v\r\nv222p040p03*p01\\p0<:vp+2/g01\\%g01:p04+1:g<\r\n>10g%\\10g/2+g \" \"- |>:::50p+>:30g\\`!#v_:\" \"\\: v\r\n|-g03::: +1< ^+g05p+2/ g01\\%g01<\r\n>$$$\"o\"9*:20p10g*:v^ $<\r\nvp050p08*9\"e\"-1p03<\r\n>:0\\:10g%\\1 v\r\n|+1:-1p+3/g0< v+1 ># v# $$< <\r\n>$\"}}P(\"***90p0>:2g:*60p0>:80g\\`!#v_:2g::**60g+:70p90g`#v_0>:80g\\`!#^_:2g:*:*70g+:90g`|\r\n |-g08:+1$ < #g%\\\"<\"%1g/#v_::\"<\"/:10g%\\10g/3+g\\\"<\"%1g+v\r\n ^+1 $<0p05+1g05p+3/g01\\%g01:/\"<\"\\ <", "Here we iterate quite simply through all the `primes[a]^2 + primes[b]^3 + primes[c]^4` combinations and remember the already found ones.\r\n\r\nThe prime numbers are generated with the help from our old friend the [Sieve of Eratosthenes](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes)\r\n*(i improved my befunge snippet for this algorithm a little bit. It\'s now a bit faster and smaller in size)*.\r\n\r\nThe main problem was that we needed an bit-array with an size of **fifty million bits**.\r\nNormally I would simply use an array of size fifty million. But we need to only store Boolean information.\r\nSo I used a \"trick\" were I stored sixty bits per cell (these are 64-bit values, but I wanted to prevent signed/unsigned problems and I had the problem that the stack is also only 64-bit).\r\nUnfortunately befunge has no bit operators. So we had to re-invent bit-setting and bit-getting with division, modulo and addition operators.\r\n\r\nIn the end this didn\'t make the program fast, but the file size is under 1MB. And I think the run time is acceptable.", 1, 181436097, 27067, 1000, 1018, 1097343);
+ Do(88, "Product-sum numbers", "A natural number, N, that can be written as the sum and product of a given set of \r\nat least two natural numbers, `{a1, a2, ... , ak}` is called a product-sum number: \r\n`N = a1 + a2 + ... + ak = a1 * a2 * ... * ak`.\r\n\r\nFor example, 6 = 1 + 2 + 3 = 1 × 2 × 3.\r\n\r\nFor a given set of size, k, we shall call \r\nthe smallest N with this property a minimal product-sum number.\r\nThe minimal product-sum numbers for sets of size, `k = 2, 3, 4, 5`, and `6` are as follows.\r\n\r\n~~~\r\nk=2: 4 = 2 * 2 = 2 + 2\r\nk=3: 6 = 1 * 2 * 3 = 1 + 2 + 3\r\nk=4: 8 = 1 * 1 * 2 * 4 = 1 + 1 + 2 + 4\r\nk=5: 8 = 1 * 1 * 2 * 2 * 2 = 1 + 1 + 2 + 2 + 2\r\nk=6: 12 = 1 * 1 * 1 * 1 * 2 * 6 = 1 + 1 + 1 + 1 + 2 + 6\r\n~~~\r\n\r\nHence for `2<=k<=6`, the sum of all the minimal product-sum numbers is `4+6+8+12 = 30`;\r\nnote that 8 is only counted once in the sum.\r\n\r\nIn fact, as the complete set of minimal product-sum numbers for `2<=k<=12`\r\nis `{4, 6, 8, 12, 15, 16}`, the sum is `61`.\r\n\r\nWhat is the sum of all the minimal product-sum numbers for `2<=k<=12000`?", "v XXXX\r\n OOOO\r\n\r\n### ... ###\r\n### ... ###\r\n### ... ###\r\n\r\n### ... ###\r\n### ... ###\r\n### ... ###\r\n\r\n vp+8+8/g05\\%g05:\\1:p+3/<\r\n>\"`` \"+*20p\"}`\"*30p8:*:*:*:*40p28*8*8*50p20g>:!#v_1-:40g\\:50g%\\50g ^\r\n vp142p13+1g03p122p+8812 $31g1+31p 082*g::41g\\/\\1+*4 1p1+082*p051p >41g31g30g21g-+`#v_30g31g41g--1`41g31g`!30g31g4 ^g--:50g%\\50g/3+g41g`++3-#^_41g30g31g41g-^\r\n ^p+3/g05\\ %g05< > 51g:50g%\\50g/82*+g:41g\\/41p3v\r\n vp15+1g15p13+\\g13p14*\\g14:g+*28/g05\\%g05:g1 5p+*28/g05\\%g05:g15g+*28/g05\\%g05:+1g15p13-\\g1<\r\n >51g30g1+-#v_ v ^ <\r\n v p13+1g13<\r\n >51g:50g%\\50g/82*+g::1+51g:50g%\\50g/82*+p 41g\\/41p1+41g*41p51g21g`#v_ ^\r\nvp310p300 < >51g21p^\r\n >3+g61g1+:50g%\\50g/3+p61g:50 v >$$v\r\n >1pv>71g- #v v# < # $_v#`\\g18<\r\n 7v0<^:g+3/g< ^ /g05\\%g05:g16g+3/g 05\\%g05:+1:p16:< >81g-|\r\n>01-^>::50g%\\50^ v_$:0\\:50g%\\5 0g/3+p^>::50g%\\50g/3+g::| $\r\n ^_v#-g02:+1<>:71g`#v_81p:>1-:1+ | # ^ $$< 1 \r\n $ ^ $># 7# 1 p# <$<0 p+3/g05\\%g05:\\0 +<\r\n v00< ^p+3/g05 \\%<\r\n v+1 <\r\n >::91p50g%\\50g/3+g+91g:30g-|\r\n >$.$@", "Let\'s say LIMIT is our maximum value of k (`12 000`).\r\n\r\nWe start with an array of size LIMIT, filled with ones.\r\nOur current sum is `LIMIT` and our current product is `1`.\r\nTo kickstart the whole progress we set `arr[1] = 2` (now sum is `LIMIT+1` and product is `2`).\r\nWe also remember the amount of changed fields, which are possible not one (initial `2`).\r\n\r\nNow we iterate through all the possible array-combinations (with a few tricks to limit the search-space).\r\n\r\n - In each step we increment array[0]. And update the fields sum and product.\r\n This update is not that complex, sum is incrementing by `1` and\r\n product is `(product / arr[0]-1) * arr[0]`\r\n - While `prod > sum + (LIMIT - len)` we reset the current `arr[pos]` to `arr[pos + 1]` \r\n and increment arr[pos + 1] \r\n (and obviously increment `pos` and update `sum` and `product`)\r\n - After that we have a valid array valud. We can now test for which value of k this is a result\r\n (and if is is better than a previous found value)\r\n - The value of k is `k := LIMIT - (sum - prod)`\r\n The trick here is that we generate a solution by cutting away a lot of the ones at the end of our array \r\n to get a solution where `prod = sum` (cutting ones decreemnts sum but leaves prod unchanged).\r\n - The condition to cut away only ones is given by our previous condition `prod > sum + (LIMIT - len)`.\r\n - After we have gone through all the possible values this way we only have calculate the sum of all the unique values\r\n \r\nBecause in the last step the list is almost sorted (not totally sorted but there arent that many cases where result[i] > result[i+1])\r\nwe can use a need little algorithm which eliminates duplicates by running through the list \r\nand doing sum occasional backtracing with an complexity of almost O(N).\r\n\r\nI know, the algorithm got a bit complex, but it\'s pretty fast - even when converted to befunge.", 1, 141097978, 23852, 1024, 50, 7587457);
+ Do(89, "Roman numerals", "For a number written in Roman numerals to be considered valid there are basic rules which must be followed.\r\nEven though the rules allow some numbers to be expressed in more than one way there is always a \"best\" way\r\nof writing a particular number.\r\n\r\nFor example, it would appear that there are at least six ways of writing the number sixteen:\r\n\r\n~~~\r\nIIIIIIIIIIIIIIII\r\nVIIIIIIIIIII\r\nVVIIIIII\r\nXIIIIII\r\nVVVI\r\nXVI\r\n~~~\r\n\r\nHowever, according to the rules only XIIIIII and XVI are valid,\r\nand the last example is considered to be the most efficient, as it uses the least number of numerals.\r\n\r\nThe 11K text file, roman.txt, contains one thousand numbers written in valid,\r\nbut not necessarily minimal, Roman numerals;\r\nsee **About... Roman Numerals** for the definitive rules for this problem.\r\n\r\nFind the number of characters saved by writing each of these in their minimal form.\r\n\r\n*Note:* You can assume that all the Roman numerals in the file contain no more \r\nthan four consecutive identical units.\r\n\r\nAbout... Roman Numerals\r\n=======================\r\n\r\n> How do you read and write Roman numerals?\r\n\r\nTraditional Roman numerals are made up of the following denominations:\r\n\r\n~~~\r\nI = 1\r\nV = 5\r\nX = 10\r\nL = 50\r\nC = 100\r\nD = 500\r\nM = 1000\r\n~~~\r\n\r\nIn order for a number written in Roman numerals to be considered valid there are three basic rules \r\nwhich must be followed.\r\n\r\nNumerals must be arranged in descending order of size.\r\n\r\n`M`, `C`, and `X` cannot be equalled or exceeded by smaller denominations.\r\n\r\n`D`, `L`, and `V` can each only appear once.\r\n\r\nFor example, the number sixteen could be written as `XVI` or `XIIIIII`,\r\nwith the first being the preferred form as it uses the least number of numerals.\r\nWe could not write `IIIIIIIIIIIIIIII` because we are making `X` (ten) from smaller denominations,\r\nnor could we write VVVI because the second and third rule are being broken.\r\n\r\nThe \"descending size\" rule was introduced to allow the use of subtractive combinations.\r\nFor example, four can be written `IV` because it is one before five.\r\nAs the rule requires that the numerals be arranged in order of size it should be clear to\r\na reader that the presence of a smaller numeral out of place, so to speak,\r\nwas unambiguously to be subtracted from the following numeral rather than added.\r\n\r\nFor example, nineteen could be written `XIX` = `X (ten) + IX (nine)`.\r\nNote also how the rule requires `X` (ten) be placed before `IX` (nine),\r\nand `IXX` would not be an acceptable configuration (descending size rule).\r\nSimilarly, `XVIV` would be invalid because `V` can only appear once in a number.\r\n\r\nGenerally the Romans tried to use as few numerals as possible when displaying numbers.\r\nFor this reason, `XIX` would be the preferred form of nineteen over other valid combinations,\r\nlike `XIIIIIIIII` or `XVIIII`.\r\n\r\nBy mediaeval times it had become standard practice to avoid more than three consecutive\r\nidentical numerals by taking advantage of the more compact subtractive combinations.\r\nThat is, `IV` would be written instead of `IIII`,\r\n`IX` would be used instead of `IIIIIIIII` or `VIIII`, and so on.\r\n\r\nIn addition to the three rules given above,\r\nif subtractive combinations are used then the following four rules must be followed.\r\n\r\n - Only one `I`, `X`, and `C` can be used as the leading numeral in part of a subtractive pair.\r\n - `I` can only be placed before `V` and `X`.\r\n - `X` can only be placed before `L` and `C`.\r\n - `C` can only be placed before `D` and `M`.\r\n\r\nWhich means that `IL` would be considered to be an invalid way of writing forty-nine,\r\nand whereas `XXXXIIIIIIIII`, `XXXXVIIII`, `XXXXIX`, `XLIIIIIIIII`, `XLVIIII`, and `XLIX`\r\nare all quite legitimate, the latter is the preferred (minimal) form.\r\nHowever, minimal form was not a rule and there still remain in Rome many examples\r\nwhere economy of numerals has not been employed.\r\nFor example, in the famous Colosseum the numerals above the forty-ninth entrance\r\nis written `XXXXVIIII` rather than `XLIX`.\r\n\r\nIt is also expected, but not required, that higher denominations should be used whenever possible;\r\nfor example, `V` should be used in place of `IIIII`, `L` should be used in place of `XXXXX`,\r\nand `D` should be used in place of `CCCCC`.\r\nHowever, in the church of Sant\'Agnese fuori le Mura (St Agnes\' outside the walls),\r\nfound in Rome, the date, `MCCCCCCVI` (1606), is written on the gilded and coffered wooden ceiling;\r\nI am sure that many would argue that it should have been written `MDCVI`.\r\n\r\nSo if we believe the adage, \"when in Rome do as the Romans do,\"\r\nand we see how the Romans write numerals, then it clearly gives us much more freedom\r\nthan many would care to admit.", "vABCDEFGHIJKLMNOPQRSTUVWXYZ\r\nv0123212342\r\n ???? ?\r\n>092p190p5492*+0p55+v\r\nvp03\"d\"p0*62\"2\"p0*83< >::1g\"0\"-\\v\r\n>\"}\"4*40p\"}\"8*94+0p55+^_v#:-1p1 -*\\ >42p 22g+22pv\r\n >$9:12p>0>:12gg48*-|^10\\_^#`\\g24::g0-\"@\"gg21:-1<:\r\n >:32p 1-:12gg\"@\"-0g:42p22p>:|<\r\n v+55\\g1 +1/+55%\"d\":\\g1+1/\"d\"%*8\"}\":\\/*8\"}\":g22$<\r\nMMMMDCLXXII >%1+1g\\ +++32g\\-92g+92pv\r\nMMDCCCLXXXIII |-+9*8\"}\":p21:+1<\r\nMMMDLXVIIII >$92g.@\r\n...\r\n...\r\n...", "I don\'t know why this problem has such a high number.\r\n\r\nWe simply parse all the roman numbers in the file and create minimal roman literals from them.\r\nThen we simply sum all the length-differences together.\r\n\r\nAnd it wasn\'t really hard to write algorithms for these two conversions. Both are pretty straight forward.\r\n(And for number->roman we didn\'t even have to go the whole way, we only need the *length* of the result)\r\n\r\nFor the conversion roman->number we first search for the length of the roman literal.\r\nThen we go backwards through the letters and get the value of each letter (cached by the array in line one).\r\nIf the value of the letter is greater than the last value we increment the total value (by the letter value),\r\notherwise we decrement it.\r\nI found it easier to traverse the number backwards because we can cache the value of the last digit and do the algorithm this way with less `g` calls.\r\n\r\nFor the conversion number->optimal_roman_length i found this nice formula:\r\n\r\n~~~\r\n(n/1000) + R[(N%1000)/100] + R[(N%100)/10] + R[N%10]\r\n\r\n// n is our number\r\n// R is defined as an array with { 0, 1, 2, 3, 2, 1, 2, 3, 4, 2 }\r\n~~~", 1, 569231, 78, 73, 1009, 743);
+ Do(90, "Cube digit pairs", "Each of the six faces on a cube has a different digit (0 to 9) written on it;\r\nthe same is done to a second cube.\r\nBy placing the two cubes side-by-side in different positions we can form a variety of 2-digit numbers.\r\n\r\nFor example, the square number 64 could be formed:\r\n\r\n~~~\r\n +-------+ +-------+\r\n / /| / /|\r\n+-------+ | +-------+ |\r\n| | | | | |\r\n| 6 | + | 4 | +\r\n| |/ | |/\r\n+-------+ +-------+\r\n~~~\r\n\r\nIn fact, by carefully choosing the digits on both cubes it is possible to display\r\nall of the square numbers below one-hundred: `01`, `04`, `09`, `16`, `25`, `36`, `49`, `64`, and `81`.\r\n\r\nFor example, one way this can be achieved is by placing `{0, 5, 6, 7, 8, 9}` on one cube \r\nand `{1, 2, 3, 4, 8, 9}` on the other cube.\r\n\r\nHowever, for this problem we shall allow the `6` or `9` to be turned upside-down \r\nso that an arrangement like `{0, 5, 6, 7, 8, 9}` and `{1, 2, 3, 4, 6, 7}` allows \r\nfor all nine square numbers to be displayed; otherwise it would be impossible to obtain `09`.\r\n\r\nIn determining a distinct arrangement we are interested in the digits on each cube, not the order.\r\n\r\n - `{1, 2, 3, 4, 5, 6}` is equivalent to `{3, 6, 4, 1, 2, 5}`\r\n - `{1, 2, 3, 4, 5, 6}` is distinct from `{1, 2, 3, 4, 5, 9}`\r\n\r\nBut because we are allowing `6` and `9` to be reversed, the two distinct sets in \r\nthe last example both represent the extended set `{1, 2, 3, 4, 5, 6, 9}` for the \r\npurpose of forming 2-digit numbers.\r\n\r\nHow many distinct arrangements of the two cubes allow for all of the square numbers to be displayed?", "v X_XXOO ######### v6$< > #g #0 #+ #8 #: #:v#<>v\r\n2 X ##########v 2+4\\1p22+g22!g2+4:< _^#-9:%+55*:p1+4\\1p12+g12!g1+4:/+55*::_v 1g\r\n9 X ##########v1+4\\1p12+g12!g1+4:< _v#-9:%+55*:p2+4\\1p22+g22!g2+4:/+55*::< 26\r\n3 C >p #^6$ #< #v ># #< 1-:|$`\r\n*>020p8>:0\\9+0p:#v_$021p022p9>:0\\4+1p:0\\4+2p:#v_$55+^vg0+9p0+9\\!g0+9::::< >^2\r\n+p ^-1 <^00 <^-1 < v$$_!#v_1- # #v #! #+^#`6g2<\r\n33 ^ < >$ ^ v_8 ^ \r\n>^ @.g02< >:1-\\#v_$ > 8^\r\n >:0\\4+1p >:1-\\#v_$ v |g1+4:<9_v#-g12 6< \r\n vp1+4\\1:<|g1+4:<9_v#-g125p1+4\\1:< 2> ^\r\n ^0 ^< >#1>:0\\4+1p >:1-\\#^_$ ^\r\n $# ^ $$ < #$\r\n >#^_1- :!#^_1- :!#^_@\r\n ! > > >22g6- #v _v \r\n >v ^: ^# < >:1-\\#v_$ #2v\r\n p >:0\\4+2p >:1-\\#v_$ v |g2+4:<9<< > v\r\n 2 vp2+4\\1:<|g2+4:<9_v#-g225p2+4\\1:< v < >g1+20pv\r\n + ^0 ^< >#1>:0\\4+2p # >:1-\\#^_$ ^ ^02p+g<\r\n 9 $# ^ #$$ < ^ $< $# >%\\\"P\"/33^\r\n>#4> :!#^_1- :!#^_1- :!#^_@^\"P\":\\g03<\r\n 0 v+64p04+g1+94!g1+64< ># #< #v# #< v #\r\n p >2g!49+2g+50pv>40g50g+#^_046+1p149+1p046+2p149+2pv>146+1p049+1p146+2p 049vv<\r\n^<^2+641< v0p2+9$0 41p2+640_v#!g05v v $# $# # < > ^ \r\n> 1+:!#^_1- :!#^_1- #^ #< :!#^_1-:!#^_@>33g+g:30g-#v_$$^ <\r\n ^ -# < 9 ^ < >57*- !| #\r\n > >060p070p9v< 9p070p060< < ^/\"P\"\\%\"P\"::< v <\r\n v*2g06g1+4:< $v < >\\v^-1<*\" (\"<#\r\n >+60p:1-\\ #^_^>:4+2g70g2*+70p:1-\\#^_$70g60g:70g`#^_>48*:**+30p^\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################\r\n################################################################################", "We have nine square numbers that need to be represented.\r\nFor each number we can either use dice one for the first digit and dice two for the second or the other way around. Together there are `2^9 (=512)` possibilities.\r\nIn our program we iterate through them all (a simple binary counter at program position [9,0]).\r\n\r\nIn each turn we remember which numbers would need to be written on the first dice and which on the second one (we have two boolean arrays at [4,1] and [4,2]). If one dice needs more than six numbers on it we can directly throw this combination away and go on with the next number in our binary counter.\r\n\r\nIt\'s important that in this phase we have no nines. Every nine is replaced with a six (so we use `3*3 = 09` and `7*7 = 46`) The nines are later taken into account.\r\n\r\nNow most of the time one or both dices have less than six digits on it (sometimes even only four).\r\nWe iterate now through all possible combinations of six digits with our found set as a basis. (So if one dice has 5 digits and the other one 4 we generate an additional 150 combinations (`5*5*6`).\r\n\r\nThen in the last step we look at each dice and see if it contains a six and no nine. If this is the case we generate another combination where the six and the nine is exchanged. (Because we do this for each dice individually we can for each given combination possibly generate four new ones *(original, D1 exchanged, D2 exchanged, both exchanged)*).\r\n\r\nNow we have every possible combinations that fits our initial condition. To weed out all the duplicates we generate a hash from the combination and remember previously found values in an 80x16 big hashmap (originally I had the map way bigger, but after my first successful run I could shrink the size to a more fitting value).\r\n\r\nThe hash is simply the binary representation of **D1** and **D2** concatenated (one for \"has this digit\", zero for \"does not have this digit\").\r\nBecause the order of the dices is irrelevant in our result we ignore it also in our hash and always use the dice with the smaller hash value as the lower bits of the total hash (this way `HASH(D1,D2) == HASH(D2,D1)`).\r\n\r\nOne problem of writing this program (except the metric fuck-ton of code all this needs, seriously I filled a 80x30 grid only with logic, there is more raw code than space for the 1280-elements hashmap) were the filling methods.\r\n\r\nIn my C# test program I had three functions:\r\n\r\n - **PadLeft** fills the left digit up to six digits with all possible values\r\n - **PadRight** fills the right digit up to six digits with all possible values\r\n - **PadNine** exchanges `6` with `9` in the left and right digit to generate all possible combinations\r\n - **Output** Test if a is already in the hashmap, if not increments the counter \r\n\r\nNow the function PadLeft() calls PadRight() which calls PadNine(), which calls Output(). Each at three to four different places.\r\nSo in my befunge program I needed to do the same thing every sane procedural language does:\r\nRemember the back jump address, so after PadNine() is called we know where in PadRight() we have to continue the program flow.\r\n\r\nUnfortunately this is in befunge not really good to write and leads to a lot of boilerplate code, but it\'s still better than writing the Output function twenty-seven times in different places.\r\n\r\nA last note: This is the first program where I put the big data structures below the actual code. It\'s nice to have all the program logic at the top of the file, but every time I address something down there the constants for the Y value take more space. This is also the reason my variables are always in the top left corner, there I can address them with only three commands (`xyg` bzw `xyp`) as long as `x` and `y` are below ten.\r\nSo I think it\'s not too bad to have the data below the code but for the future I will keep my old organization.", 0, 335326352, 54366, 80, 45, 1217);
+ Do(91, "Right triangles with integer coordinates", "The points `P(x1, y1)` and `Q(x2, y2)` are plotted at integer co-ordinates and are joined to the origin,\r\n`O(0,0)`, to form `OPQ`.\r\n\r\n\r\n\r\nThere are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate \r\nlies between 0 and 2 inclusive; that is,\r\n\r\n~~~\r\n0 <= x1, y1, x2, y2 <= 2.\r\n~~~\r\n\r\n\r\n\r\nGiven that `0 <= x1, y1, x2, y2 <= 50`, how many right triangles can be formed?", "\"2\":11p031p41p>11g51p51g1> #1 #g #$41p#^_31g311g:**+.@>$p v1+\r\n>1g51g:61g-\\*41g%!2*+31p61g1+61pv!56\r\n^ >51g#^ #:1# - #1:#g5#11#4 ^# _^1\r\n^3_^#! +`g11g16`*:g14*-\\g16:g15< p<", "This was mostly a mathematical problem.\r\n\r\nLets go step by step through my solution:\r\n\r\nWe have a triangle with three corners, `O(o_x, o_y)`, `Q(q_x, q_y)` and `P(p_x, p_y)`, where `O = (0,0)`.\r\nWe can quickly see that there are three types of solutions, triangles where O has the right angle, \r\ntriangles where Q has the right angle and triangles where P has the right angle.\r\n\r\nThe amount of triangles in group two (angle at Q) and group three (angle at P) are identical (!)\r\nBecause for every triangle in group two there is a triangle in group three which has the points P and Q mirrored at the vertical Axis `(1, 1)`.\r\nSo when we have a triangle `O(0, 0); Q1(q1_x, q1_y); P(p1_x, p1_y)` the corresponding mirrored triangle is\r\n~~~\r\nq2_x = q1_y\r\nq2_y = q1_x\r\np2_x = p1_y\r\np2_y = p1_x\r\n~~~\r\n\r\nThese two groups (two and three) are also mutually exclusive, because if `Q1 == P2` and `Q2 == P1` then the vectors `OP` and `OQ` would have equal length and \r\nthe only possible right angle could be at point O (and not at P or Q).\r\n\r\nNow that we have proven that `count(group_2) == count(group_3)` we only have to find that triangle count and the amount of triangles in group one.\r\n\r\nFirst group one:\r\n\r\nTo have an right angle at the zero point `O(0, 0)` both other points have to lie on an axis.\r\nWe say point Q lies on the x-axis and point P on the Y-axis. All combinations lead to valid and unique triangles, the only disallowed point is the origin `(0, 0)`.\r\nSo we have `SIZE` possible positions on the x-axis and `SIZE` possible positions on the y-axis. This leads to `SIZE * SIZE` different unique triangles:\r\n\r\n~~~\r\ncount(group_1) = SIZE * SIZE\r\n~~~\r\n\r\nNow group 2/3\r\n\r\nBecause we need to define a bit of semantics we say our point Q is the lower-right point of the triangle (and P is the upper left), \r\nsimilar to the project-euler example image. Also we want our right angle to be at point Q (between the vectors OP and PQ).\r\nFirst we can look at the trivial triangles, the ones where Q lies on the x-axis and P has the same x-coordinate as Q. \r\nThese triangles all have an right angle at Q and are valid solutions. And because there are `SIZE` possible positions for Q (all x-axis positions except `(0,0)`) \r\nand for each of these there are `SIZE` possible positions for P (all points on the same x-value as Q, except `y = 0`) \r\nthere are `SIZE*SIZE` trivial triangles with an right angle at Q.\r\n\r\n~~~\r\ncount(group_2_triv) = count(group_3_triv) = SIZE * SIZE\r\n~~~\r\n\r\nFor the remaining triangle we can finally - kind of - start programming.\r\nWe go through all remaining points (q_x, q_y) where `q_x > 0 && q_y > 0` (because the axis are already covered by our trivial cases).\r\n\r\nFor every point (that we assume is Q) we calculate the vector OQ:\r\n\r\n~~~\r\noq_x = q_x - 0 // trivial, yeah i know. In the final program this is all optimized away\r\noq_y = q_y - 0\r\n~~~\r\n\r\nAnd we calculate the direction of the vector QP (under the assumption that Q has a right angle and thus OQ and QP form a right angle). \r\nThis is simply the vector OQ rotate by 90° CW:\r\n\r\n~~~\r\nv_qp_x = -oq_y;\r\nv_qp_y = oq_x;\r\n~~~\r\n\r\nNow we search for integer solutions of `P = Q + n * v_QP`. Each solution, that also falls in our SIZE bounds is a valid triangle.\r\nTo find these we go through all the possible y locations out point P can have.\r\nIt is not possible that one p_y value responds to multiple p_x values, because then QP would be horizontal \r\nand these triangles are already acknowledged in our trivial cases of group_2 / group_3.\r\n\r\nSo for each (possibly valid) p_y value we can calculate the corresponding p_x value:\r\n\r\n~~~\r\np_y = q_y + n * v_qp_y\r\nn = (p_y - q_y) / v_qp_y\r\n\r\np_x = q_x + n * v_qp_x\r\n = q_x + ((p_y - q_y) / v_qp_y) * v_qp_x\r\n = q_x + ((p_y - q_y) * v_qp_x / v_qp_y)\r\n~~~\r\n\r\nFirst we want to test if `(p_y - q_y) * v_qp_x` is a multiple of `v_qp_y`. \r\nIf this were not the case than p_x is not an integer and this is not an integer solution \r\n(then we would simply continue with the next y value until y > SIZE and we have reached our limit).\r\nBut if P(p_x, p_y) **has** two integer components we only need to test if p_x is greater than zero \r\n(because otherwise the triangle would be out of our defined bounds) and then we can increment out triangle counter.\r\nBe aware that we have in this step practically found two unique triangles, this one and its mirrored counter part (see explanation at the beginning).\r\nNow we continue our looping, first until we have tested all possible p_y values (until p_y grows greater than our bounds, SIZE) \r\nand then until we have tested all valid points for Q.\r\n\r\nIn the end we only have to add our values together and we have our result:\r\n\r\n~~~\r\nresult = c_group_1 + 2 * c_group_23\r\n\r\nc_group_23 = c_group_23_triv + c_group_23_nontriv\r\n~~~\r\n\r\nThis is one of the problems that translate **really** well into befunge, because there are no big data structures and not even a lot of calculations. \r\nMost of the work is done before we start to write code and the challenge is finding the correct approach.\r\n\r\n*After note:* I really want a price or something for the compression of this program.\r\nEverything is crunched into a 36x5 rectangle and there are nearly no unused codepoints...", 0, 3072923, 343, 36, 5, 14234);
+ Do(92, "Square digit chains", "A number chain is created by continuously adding the square of the digits in a number to \r\nform a new number until it has been seen before.\r\n\r\nFor example,\r\n\r\n44 ? 32 ? 13 ? 10 ? 1 ? 1\r\n85 ? 89 ? 145 ? 42 ? 20 ? 4 ? 16 ? 37 ? 58 ? 89\r\n\r\nTherefore any chain that arrives at 1 or 89 will become stuck in an endless loop. \r\nWhat is most amazing is that EVERY starting number will eventually arrive at 1 or 89.\r\n\r\nHow many starting numbers below ten million will arrive at 89?", "v $$ T # #######################################################################\r\n # #######################################################################\r\n XX # #######################################################################\r\n # #######################################################################\r\n # #######################################################################\r\n # #######################################################################\r\n # #######################################################################\r\n # #######################################################################\r\n\r\n v p1*93\"Y\" p0+551 $<\r\n> \"G\"8*:32p\"}2((\"***22p020p030p >1-:0\\:\"G\"%9+\\\"G\"/p:!|\r\n v pp02+1:g027:$<^ ># v# <\r\n >22g:>:32g`#v_::\"G\"%9+\\\"G\"/g:!#^_:1-!#v_ :\"Y\"-| # >1-:20p7\\g50g\\: v\r\n >0\\>:55+%:*\\ :#v_$$11v >30g1+30p>50p$20g:|:g02p/\"G\"\\+9%\"G\"<\r\n >3 v^/+55g05+p05< >$@ v1 ::-1$<\r\n ^_^# _^#># 0# g# .# $# ^# <*0 <", "My approach to this problem is pretty crude. Perhaps I will later come back and try to find a better algorithm.\r\nCurrently we iterate (brute-force) through all possible numbers and count the chains that end with one.\r\nThe `next()` function is implemented like this:\r\n\r\n~~~~~~~~~~~~~~~~~~~\r\n0\\>:55+%:*\\ :#v_$$\r\n ^/+55g05+p05< \r\n~~~~~~~~~~~~~~~~~~~\r\n\r\nWe also remember in an 8x71 cache all previously found numbers so we can abort some sequences before we reach `1` or `89`.\r\nThis is the main optimization from pure brute-force in this program.\r\n\r\nWe can prove that an 568-element cache is enough because no number in the sequence (except the first) can be greater than `9^2 * 7` (` = 567`)", 0, 2959813630, 379925, 80, 16, 8581146);
+ Do(93, "Arithmetic expressions", "By using each of the digits from the set, `{1, 2, 3, 4}`, exactly once, \r\nand making use of the four arithmetic operations (`+`, `?`, `*`, `/`) and brackets/parentheses, \r\nit is possible to form different positive integer targets.\r\n\r\nFor example,\r\n\r\n~~~\r\n8 = (4 * (1 + 3)) / 2\r\n14 = 4 * (3 + 1 / 2)\r\n19 = 4 * (2 + 3) ? 1\r\n36 = 3 * 4 * (2 + 1)\r\n~~~\r\n\r\nNote that concatenations of the digits, like `12 + 34`, are not allowed.\r\n\r\nUsing the set, {1, 2, 3, 4}, it is possible to obtain thirty-one different target numbers \r\nof which 36 is the maximum, and each of the numbers 1 to 28 can be obtained \r\nbefore encountering the first non-expressible number.\r\n\r\nFind the set of four distinct digits, `a < b < c < d`, for which the \r\nlongest set of consecutive positive integers, 1 to n, can be obtained, \r\ngiving your answer as a string: abcd.", "v XXXX ####################################################################################################\r\n XX ####################################################################################################\r\n ####################################################################################################\r\n C ####################################################################################################\r\n OOOO ####################################################################################################\r\n ####################################################################################################\r\n OOOO O ####################################################################################################\r\n OOOO O ####################################################################################################\r\n OOOO O ####################################################################################################\r\n OOOO O ####################################################################################################\r\n ################ ... ... ... ... ################\r\n0 ####################################################################################################\r\n2 ####################################################################################################\r\n1 ####################################################################################################\r\np ####################################################################################################\r\n\" ####################################################################################################\r\nH ####################################################################################################\r\n# ####################################################################################################\r\n\" ####################################################################################################\r\n* ####################################################################################################\r\n2 ####################################################################################################\r\n3 ####################################################################################################\r\np ####################################################################################################\r\n0 ####################################################################################################\r\n3 ####################################################################################################\r\n1 ####################################################################################################\r\np ####################################################################################################\r\n\r\n>\"}P\"*>1-:\" \"\\:\"d\"v\r\n |:p/\"d\"\\+9% <\r\nv $< >4g.24g.34g.44g.@\r\n>120p>20g1+30p >30g1+40p >40g1+50p > \"X\" 20g55+*30g+50g55+*40v\r\n |-7p02:+1g02<|-8p03:+1g03<|-9p04:+1g04<|-5-5p05:+1g05p13+1g13p+g <\r\nv < # ^< ^< ^<\r\n> 31g1-!#^_21g1+21p031p>120p>20g1+30p >30g1+40p >40g1+50p >20g55+*30g+50g55+*40g+g\"X\"-v\r\n |-7p02:+1g02<|-8p03:+1g03<|-9p04:+1g04<|-5-5p05:+1g05< _v\r\n^ < ^< ^< ^< >^\r\n vp670p64*g32g05p63*g32g04p62*g32g03p61*g32g02 ># ^# <\r\n v 76g:1+76pv >77g:1+77pv >78g:1+78pv ^\r\n> #v #: #< #v #: #< ^ v: <\r\n v-1_$077p16g26g+17p36g27p46g37p ^v-1_$078p17g27g+18p37g28p ^v-1_$18g28g+19p v\r\n >: v >: v >: v\r\n v-1_$077p16g36g+17p26g27p46g37p ^v-1_$078p17g37g+18p27g28p ^v-1_$18g28g-19p v\r\n >: v >: v >: v\r\n v-1_$077p16g46g+17p26g27p36g37p ^v-1_$078p37g18p27g17g+28p ^v-1_$28g18g-19p v\r\n >: v >: v >: v\r\n v-1_$077p46g17p26g16g+27p36g37p ^v-1_$078p17g18p27g37g+28p ^v-1_$18g28g*23g/19p v\r\n >: v >: v >: v\r\n v-1_$077p16g17p26g36g+27p46g37p ^v-1_$078p27g18p37g17g+28p ^v-1_$28g!#v_18g23g*28g/19p v\r\n >: v >: v >: v > ^\r\n v-1_$077p16g17p26g46g+27p36g37p ^v-1_$078p17g18p37g27g+28p ^v $_$18g!#v_28g23g*18g/19p v\r\n >: v >: v ^ < > ^\r\n v-1_$077p46g17p26g27p36g16g+37p ^v-1_$078p17g27g-18p37g28p ^ <\r\n >: v >: v |+!!%g32g91!!-g12/g32g91<\r\n v-1_$077p16g17p46g27p36g26g+37p ^v-1_$078p17g37g-18p27g28p ^ 3\r\n >: v >: v 1\r\n v-1_$077p16g17p26g27p36g46g+37p ^v-1_$078p37g18p27g17g-28p ^ g\r\n >: v >: v 1\r\n v-1_$077p36g17p26g27p46g16g+37p ^v-1_$078p17g18p27g37g-28p ^ +\r\n >: v >: v 3\r\n v-1_$077p16g17p36g27p46g26g+37p ^v-1_$078p27g18p37g17g-28p ^ 1\r\n >: v >: v p\r\n v-1_$077p16g17p26g27p46g36g+37p ^v-1_$078p17g18p37g27g-28p ^ 2\r\n >: v >: v 0\r\n v-1_$077p16g26g-17p36g27p46g37p ^v-1_$078p17g27g*23g/18p37g28p ^ g\r\n >: v >: v 1\r\n v-1_$077p16g36g-17p26g27p46g37p ^v-1_$078p17g37g*23g/18p27g28p ^ 4\r\n >: v >: v p\r\n v-1_$077p16g46g-17p26g27p36g37p ^v-1_$078p37g18p27g17g*23g/28p ^ 3\r\n >: v >: v 0\r\n v-1_$077p46g17p26g16g-27p36g37p ^v-1_$078p17g18p27g37g*23g/28p ^ g\r\n >: v >: v 2\r\n v-1_$077p16g17p26g36g-27p46g37p ^v-1_$078p27g18p37g17g*23g/28p ^ 4\r\n >: v >: v p p\r\n v-1_$077p16g17p26g46g-27p36g37p ^v-1_$078p17g18p37g27g*23g/28p ^ 4\r\n >: v >: v ^44g05p4 3g0<\r\n v-1_$077p46g17p26g27p36g16g-37p ^v-1_$27g!#v_078p17g23g*27g/18p37g28p ^\r\n >: v >: v > ^\r\n v-1_$077p16g17p46g27p36g26g-37p ^v-1_$27g!#v_078p17g23g*37g/18p27g28p ^\r\n >: v >: v > ^\r\n v-1_$077p16g17p26g27p36g46g-37p ^v-1_$27g!#v_078p37g18p27g23g*17g/28p ^\r\n >: v >: v > ^\r\n v-1_$077p36g17p26g27p46g16g-37p ^v-1_$27g!#v_078p17g18p27g23g*37g/28p ^\r\n >: v >: v > ^\r\n v-1_$077p16g17p36g27p46g26g-37p ^v-1_$27g!#v_078p27g18p37g23g*17g/28p ^\r\n >: v >: v > ^\r\n v-1_$077p16g17p26g27p46g36g-37p ^v $_$27g!#v_078p17g18p37g23g*27g/28p ^\r\n >: v ^ < > ^\r\n v-1_$077p16g26g*23g/17p36g27p46g37p ^\r\n >: v\r\n v-1_$077p16g36g*23g/17p26g27p46g37p ^\r\n >: v\r\n v-1_$077p16g46g*23g/17p26g27p36g37p ^\r\n >: v\r\n v-1_$077p46g17p26g16g*23g/27p36g37p ^\r\n >: v\r\n v-1_$077p16g17p26g36g*23g/27p46g37p ^\r\n >: v\r\n v-1_$077p16g17p26g46g*23g/27p36g37p ^\r\n >: v\r\n v-1_$077p46g17p26g27p36g16g*23g/37p ^\r\n >: v\r\n v-1_$077p16g17p46g27p36g26g*23g/37p ^\r\n >: v\r\n v-1_$077p16g17p26g27p36g46g*23g/37p ^\r\n >: v\r\n v-1_$077p36g17p26g27p46g16g*23g/37p ^\r\n >: v\r\n v-1_$077p16g17p36g27p46g26g*23g/37p ^\r\n >: v\r\n v-1_$077p16g17p26g27p46g36g*23g/37p ^\r\n >: v\r\n v-1_$26g!#v_077p16g23g*26g/17p36g27p46g37p ^\r\n >: v > ^\r\n v-1_$36g!#v_077p16g23g*36g/17p26g27p46g37p ^\r\n >: v > ^\r\n v-1_$46g!#v_077p16g23g*46g/17p26g27p36g37p ^\r\n >: v > ^\r\n v-1_$16g!#v_077p46g17p26g23g*16g/27p36g37p ^\r\n >: v > ^\r\n v-1_$36g!#v_077p16g17p26g23g*36g/27p46g37p ^\r\n >: v > ^\r\n v-1_$46g!#v_077p16g17p26g23g*46g/27p36g37p ^\r\n >: v > ^\r\n v-1_$16g!#v_077p46g17p26g27p36g23g*16g/37p ^\r\n >: v > ^\r\n v-1_$26g!#v_077p16g17p46g27p36g23g*26g/37p ^\r\n >: v > ^\r\n v-1_$46g!#v_077p16g17p26g27p36g23g*46g/37p ^\r\n >: v > ^\r\n v-1_$16g!#v_077p36g17p26g27p46g23g*16g/37p ^\r\n >: v > ^\r\n v-1_$26g!#v_077p16g17p36g27p46g23g*26g/37p ^\r\n >: v > ^\r\n v $_$36g!#v_077p16g17p26g27p46g23g*36g/37p ^\r\n^ ># #< ^\r\n >\" \"20g55+*30g+50g55+*40g+p^", "This one needs a little bit of a bigger explanation:\r\n\r\nFirst let me say that I\'m aware that this is neither the fastest algorithm nor the best algorithm to represent in funge-space. But its reasonable fast and I liked the challenge of doing such a big program (in terms of raw code size) in befunge.\r\n\r\nFirst we take a 4-dimensional cache of all possible number combinations (so an `bool[10][10][10][10]` array) where we remember if a combination is valid.\r\nIn our program we represent it as an 2D-field with `X=s1*10+s2` and `Y=s4*10+s3`.\r\n\r\nInitially we set all fields to true where `0 n*C = n*A + n*B\r\n~~~\r\n\r\nA little more attention is needed when doint multiplication and division, for the first we have to divide by the factor after the operation and for the second we have to multiply it:\r\n\r\n~~~\r\nC = A*B => n*C = (n*A * n*B) / n\r\nC = A/B => n*C = ((n*A)*n / (n*B)\r\n~~~\r\n\r\nIt is important that we multiply the dividend by the factor and not the result of the division, otherwise the decimal places will get lost.\r\n\r\nAs usual a final note from me: Nice problem. 10/10 would solve again", 1, 305514916, 42167, 111, 211, 1258);
+ Do(94, "Almost equilateral triangles", "It is easily proved that no equilateral triangle exists with integral length sides and integral area. \r\nHowever, the almost equilateral triangle 5-5-6 has an area of 12 square units.\r\n\r\nWe shall define an almost equilateral triangle to be a triangle \r\nfor which two sides are equal and the third differs by no more than one unit.\r\n\r\nFind the sum of the perimeters of all almost equilateral triangles with integral side lengths \r\nand area and whose perimeters do not exceed one billion (1,000,000,000).", "\"}}2( \"****04003pp201p102p>04g01g2*`#v_v\r\nXv2*2g10**!%3*g20-2g10!-1%3*g102`2g10< 0\r\nX>-*03g+03p01g2*3%2-!01g2+# 02g*3%v 3\r\nXv*2g10+*2g20g10p30+g30*+* g1022*!< @.g<\r\nC>02g3*+01p02p ^", "Nothing much to say about this one, we play a bit with the triangle formulas until we reach something that looks like a [Pell equation](https://en.wikipedia.org/wiki/Pell%27s_equation).\r\nMy approach is basically the same as the one on [mathblog.dk](http://www.mathblog.dk/project-euler-94-almost-equilateral-triangles/), but he explains it better.\r\n(And I improved my approach a bit after I read his article, his math skills are pretty good :D).\r\n\r\nThe code is in a way interesting because it only has a single conditional operator.\r\nI could remove two conditional by multiplying the increment with the normalized condition (`0`|`1`).\r\nThis way `if (condition) { x += increment; }` becomes ` x += (int)(condition) * increment`, \r\nwhich is a neat way to safe a bit of space in our program (and the resulting 40x5 code is pretty compact)", 0, 2009, 0, 40, 5, 518408346);
+ Do(95, "Amicable chains", "The proper divisors of a number are all the divisors excluding the number itself.\r\nFor example, the proper divisors of 28 are 1, 2, 4, 7, and 14.\r\nAs the sum of these divisors is equal to 28, we call it a perfect number.\r\n\r\nInterestingly the sum of the proper divisors of 220 is 284 and the sum of the\r\nproper divisors of 284 is 220, forming a chain of two numbers.\r\nFor this reason, 220 and 284 are called an amicable pair.\r\n\r\nPerhaps less well known are longer chains.\r\nFor example, starting with 12496, we form a chain of five numbers:\r\n\r\n~~~\r\n12496 -> r -> 15472 -> 14536 -> 14264 (-> 12496 -> ...)\r\n~~~\r\n\r\nSince this chain returns to its starting point, it is called an amicable chain.\r\n\r\nFind the smallest member of the longest amicable chain with no element exceeding one million.", "v # ## .... ## ## .... ##\r\n X # ## ## ## ##\r\n XXX # \r\n XX # . . . .\r\n X # . . . .\r\n X # . . . .\r\n # . . . .\r\n # \r\n # ## .... ## ## .... ##\r\n CCC # ## ## ## ##\r\n\r\n>\"}\"8*19p\"q\"9*29p\"}}@\"**39p012p014p39g15p39g>1-:0\\:19g/9+\\19g%p v\r\nv < |:p%g91\\+g92/g91:\\0:<\r\n1 v+1p%g91\\+g92 /g91:\\+g31g%g91\\+g92/g91 ::<\r\n>:13p2>:13g*:39g\\`#^ #$ #< |\r\n^_$# 6# v# -g93:+1$$< vp51g\\7:<\r\nv < >v>g+\\19g%g22pv >v >v >v > v\r\n> :23p :19g/9+\\19g%g!|> 23g:70p11v >22g:0`|>:39g\\`|>:23g-|$ >:7\\g22g-| # > 32g14p:7\\g15pv\r\n| -g93:+1 g32 < $< < <0 ^ < >131p:12g\\-32p32g14g`||*g13`\\g51g\\7:<\r\n>$15g.@ ^92/g91:p2< ^p22g%g< >31p032p0^ < v \r\n >9g%p22g:19g/29g+\\19^ v< |-g21:+1 < < \r\n ^ < <|g13$< < \r\n ^1\\+9/g91:\\1pp21+1:g217:g22<_^#!g%g91\\+9/g91:g22<", "The trick is to use a sieve to pre-calculate all the proper-divisor-sums.\r\nWe use a big 1000x1000 array to store all the proper-divisor-sums of all numbers from one to one million.\r\nInitially we set all these fields to zero, then we add `1` to all multiples of `1`, the `2` to all multiples to `2` etc, etc.\r\nAt the end we have a nice map of all the interesting numbers. (Fun fact: we have also calculated the primes, every number for which the sum is `1` is prime).\r\n\r\nThen we use a second 1000x1000 array to remember the values we have already checked.\r\nThe rest is simply iterating through all the numbers, trying to build a chain for each one and remembering the length of the longest chain together with its smallest member.\r\nWhile doing this we track the visited values in our cache array to prevent checking the same chain multiple times.\r\n\r\nThis code is not the fastest in befunge, but I honestly can\'t see a way to gain big performance (the same code in C# runs in 107ms).\r\nMost of the time is spend with building the map of the amicable values, but all approaches with calculating them on-demand where way worse than this algorithm.", 1, 1053466251, 242737, 2017, 1035, 14316);
+ Do(96, "Su Doku", "Su Doku (Japanese meaning number place) is the name given to a popular puzzle concept.\r\nIts origin is unclear, but credit must be attributed to Leonhard Euler\r\nwho invented a similar, and much more difficult, puzzle idea called Latin Squares.\r\nThe objective of Su Doku puzzles, however, is to replace the blanks (or zeros)\r\nin a 9 by 9 grid in such that each row, column, and 3 by 3 box contains\r\neach of the digits 1 to 9.\r\nBelow is an example of a typical starting puzzle grid and its solution grid.\r\n\r\n~~~~~~~~~~~~~~~~~~~~~\r\n0 0 3 0 2 0 6 0 0\r\n9 0 0 3 0 5 0 0 1\r\n0 0 1 8 0 6 4 0 0\r\n\r\n0 0 8 1 0 2 9 0 0\r\n7 0 0 0 0 0 0 0 8\r\n0 0 6 7 0 8 2 0 0\r\n\r\n0 0 2 6 0 9 5 0 0\r\n8 0 0 2 0 3 0 0 9\r\n0 0 5 0 1 0 3 0 0\r\n~~~~~~~~~~~~~~~~~~~~~\r\n\r\n~~~~~~~~~~~~~~~~~~~~~\r\n4 8 3 9 2 1 6 5 7\r\n9 6 7 3 4 5 8 2 1\r\n2 5 1 8 7 6 4 9 3\r\n\r\n5 4 8 1 3 2 9 7 6\r\n7 2 9 5 6 4 1 3 8\r\n1 3 6 7 9 8 2 4 5\r\n\r\n3 7 2 6 8 9 5 1 4\r\n8 1 4 2 5 3 7 6 9\r\n6 9 5 4 1 7 3 8 2\r\n~~~~~~~~~~~~~~~~~~~~~\r\n\r\nA well constructed Su Doku puzzle has a unique solution and can be solved by logic,\r\nalthough it may be necessary to employ \"guess and test\" methods in order to eliminate\r\noptions (there is much contested opinion over this).\r\nThe complexity of the search determines the difficulty of the puzzle;\r\nthe example above is considered easy because it can be solved by straight forward\r\ndirect deduction.\r\n\r\nThe 6K text file, [sudoku.txt](https://projecteuler.net/project/resources/p096_sudoku.txt) (right click and \'Save Link/Target As...\'),\r\ncontains fifty different Su Doku puzzles ranging in difficulty,\r\nbut all with unique solutions (the first puzzle in the file is the example above).\r\n\r\nBy solving all fifty puzzles find the sum of the 3-digit numbers found in the top\r\nleft corner of each solution grid; for example, 483 is the 3-digit number found in the\r\ntop left corner of the solution grid above.", "v XX X ########### ########### ############################# ############################# 003 ... 007\r\n C C # 3 17# # # # # # # 900 ... 000\r\n PPPPP # 15 9 8# # # # # # # 001 ... 500\r\n XXX # 6 # # # # # # # . . . . \r\n LLLLLL #1 7 # # # # # # # . . . \r\n PMMMM # 9 2 # # # # ########## # # # . . . . \r\n MM MMM # 5 4# # # # ################## # # # 002 ... 000\r\n0XXX XX # 2 # # # # ################## # # # \r\n7 #5 6 34 # # # # ####################### # # # \r\n7 #34 2 # # # # ####################### # # ####### # \r\n* ########### ###########v<# #################### # # ############ # \r\n> #v # 492*+11p9:*:9*61p>1-v## ################ # # ################# # \r\n >9+\\9/1+p:0\\:9%11g+\\9/1+p:| # ############ # # ################# # \r\n ^%9:\\+*86%+88 g+1/9\\+9%9::$#:< # ############ # # ######## ######## # \r\nv1/*93\\+*75%*93:\\0:-1+p:0\\:39*%89*+\\39*/#| 1#:+# p# < # #################### # # ################# # \r\nv p030$<>p152p::9%v # ####################### # # ############### # \r\n>9:*>1-:9/32p:9%22p212^vg+1/9\\+9< # ####################### # # ############ # \r\nv10 $< > v>68*-:42pv # ####################### # # ####### # \r\n4 ^_^#: # 1-:9%24p:9/3v^_ v # ########## # # # \r\n>30g9:*-!#^_9:*^ > #4 v# ########## # # # \r\n v0p450_v#!-*86 g+g431+g429p<$ ## # # #v <\r\n > > :#^_$14g#v_015p v # # # # v _$:1+|\r\n^ p410< ## # # #1>+\\g13g9 %9+13g9/1+p:^ v<\r\np6 v:p45+1g44 < > ^# # # #-^+**882* 9/5g06%9g31+*9< $ \r\n4>4p9 >1-:44p57*24g3*44g3%+v # # # # >:60p99*>1-::13p9/60g5%^ . \r\n1 #>|:_v#g++/3g44*3g431+ < ############################# ############################# ^ < \\++-*86<@ \r\n0 $ >64g1+64p ^|^ #># #<:77*-!#^_\\91g68*-55+*55v \r\n ^ < $# #< >025p035p045p9:*:*55p9:*>1-: 9%16p:9/26p916gvv+-*86g1+< \r\n >64g:!#v_1-#^_14g1+14pv#> >42g68*+22g9+3 v ^ < v _v#!g54 $_^#!:<_v#<-*86g+g621+<>55+*56+1g^ \r\n v $$32p54g42p20g5v- >1-:13p\"X\"57*22g3*13g3%++132g3*13g3v >p11g2 5 g+v! ! >1+:66p57*16g3*66g1-3%v \r\n >>01-::17p27p37p9:*v_$ 9v 21 vg++/3g31*3g231++%3g31*3g22*98p++/< vp210p+g 5 31<5>pv < _v#g++/3-1g66*3g621++< \r\n v94p76/9:p75%9:-1<^:<<: p v _52g89*22g3*13g3%v >25g22p3 5 gv 56 : - >56g1+56p4 v \r\n >2*+57g+167g+g20g- |p: > ^:|:p++/3g31*3g231++< ^ p24g54p 2 3< g4 >9^|+!`g51g66!!g6< p \r\n v*86g+g761+g759<7* >$9>1-:23p\"X\"57*23g3*42g1-3%++132g3*42g1-3v 5^g66 <> ^5 \r\n >-17p57g27 p67g3^* # vg++/3-1g24*3g231++%3-1g24*3g32*98p++/< >6g`!+#^_16g25p26g35p46g45p56g5^ \r\n v*98p76/*93:p75%*93:-1< _$ v>^v _52g89*23g3*42g1-3%v v ># ^#< \r\n >57g+167g+g20g-! #v_:^< 2 >:|:p++/3-1g24*3g231++< \r\n v75*750p+g761+g75*980< :: 0v19$<>p\"X\"57*22g3*42g1-3%+ + 133g3*42g1-3/++v \r\n >167g3/+g 68*-!| g>-:33^vg++/3-1g24*3g331++% 3 -1g24*3g22*98p < \r\n ^+/3g759g+167g+p^>7g3/+p30g1-30p^ - |:< p++/3-1g24*3g331++< \r\n vp51g71p+g731+g72+*2940p02 < >$9>1-::3%23p3/33p\"X\"57 * 22g3/3*23g+3*42g1-3%++132g3/3*33g+3*42gv\r\n ^ ># # ^ v># #<^ vg++/3-1g24*3+g33* 3 /3g231++%3-1g24*3+g32*3/3g22*98p++/3-1 <\r\n^ $_^#!:g21$< v :_52g89*22g3/3*23g+ 3 *42g1-3%v\r\n ^># ## #< ^", "This problem boils down to implementing a sudoku solver.\r\nSo thats what I did (initially as a stand-alone project).\r\nAnd then I wrote a program around that inputs the 5 puzzles \r\ninto the solver and calculates the result.\r\n\r\nThis means in this post I\'m trying to describe how to build a sudoku solver in befunge.\r\n\r\nBecause all the logic is practically a stand-alone sudoku solver, I simply wrote one. You can read about the development and a few of my design decisions in [this blogpost here](https://www.mikescher.com/blog/9/A_complete_sudoku_solver_in_Befunge93).\r\nThe rest was looping 50 times through the solver code and adding the results together.\r\n\r\nReally all the interesting stuff is written in the blogpost about the sudoku solver, go read it!", 1, 583893708, 90918, 218, 50, 24702);
+ Do(97, "Large non-Mersenne prime", "The first known prime found to exceed one million digits was discovered in 1999, \r\nand is a Mersenne prime of the form `2^6972593?1`;\r\nit contains exactly 2,098,960 digits. \r\nSubsequently other Mersenne primes, of the form `2^p?1`, have been found which contain more digits.\r\n\r\nHowever, in 2004 there was found a massive non-Mersenne prime which contains 2,357,207 digits: `28433*2^7830457+1`.\r\n\r\nFind the last ten digits of this prime number.", "\"z~k\"+*7+98v@\r\nv +***\"Gqz\"<.\r\n>1- \\2*\"(2\"v%\r\n|: \\%*:** :<*\r\n>$1+\"(2\":**:^", "Well this was a really easy one.\r\nWe simply multiply the number `28433` 7830457-times with two.\r\nAfter each multiplication we modulo the result with 2^10 to prevent an overflow and in the end we add one.\r\nThis is really simple (the program operates completely on the stack) and works perfectly as long as our interpreter uses at least 64bit numbers.\r\n(But this is a condition for a lot of programs I have written here)\r\n\r\nBut just for fun I have written an alternative version that uses only 32bit numbers.\r\nYou can find it on github under `Euler_Problem-097 (32bit).b93`, or here:\r\n\r\n~~~~~~~~~~~~\r\n\"}}2( \"****04003pp201p102p>04g01g2*`#v_v\r\nXv2*2g10**!%3*g20-2g10!-1%3*g102`2g10< 0\r\nX>-*03g+03p01g2*3%2-!01g2+# 02g*3%v 3\r\nXv*2g10+*2g20g10p30+g30*+* g1022*!< @.g<\r\nC>02g3*+01p02p ^\r\n~~~~~~~~~~~~", 0, 164439636, 21091, 13, 5, 8739992577);
+ Do(98, "Anagramic squares", "By replacing each of the letters in the word CARE with 1, 2, 9, and 6 respectively, \r\nwe form a square number: 1296 = 36^2. What is remarkable is that, \r\nby using the same digital substitutions, the anagram, RACE, \r\nalso forms a square number: 9216 = 96^2. \r\nWe shall call CARE (and RACE) a square anagram word pair and specify further \r\nthat leading zeroes are not permitted, \r\nneither may a different letter have the same digital value as another letter.\r\n\r\nUsing [words.txt](https://projecteuler.net/project/resources/p098_words.txt), \r\na 16K text file containing nearly two-thousand common English words, \r\nfind all the square anagram word pairs \r\n(a palindromic word is NOT considered to be an anagram of itself).\r\n\r\nWhat is the largest square number formed by any member of such a pair?\r\n\r\nNOTE: All anagrams formed must be contained in the given text file.", "vXXX # #################################################################################################### # A\r\n XXX # #################################################################################################### # ACCESS\r\n XX # #################################################################################################### # ACROSS\r\n XX # #################################################################################################### # ADDITIONAL\r\n XXX # #################################################################################################### # ADVISE\r\n X # #################################################################################################### # AGAINST\r\n # #################################################################################################### # AIM\r\n # #################################################################################################### # ALRIGHT\r\n # #################################################################################################### # ANALYSIS\r\n $ # #################################################################################################### # ANYBODY\r\n #################################################################################################### # APPEARANCE\r\n #################################################################################################### # ARGUE\r\n #################################################################################################### # ART\r\n #################################################################################################### # ASSET\r\n #################################################################################################### # ATTEMPT\r\n0 #################################################################################################### # AVAILABLE\r\n1 #################################################################################################### # BACKGROUND\r\n9 #################################################################################################### # BASIC\r\np v \\< v !:\\< # BED\r\n>0>:: 0\\ :9%82**\"r\"+\\9/ 10p>:1+\\10gg:84*-#^_$$ 0\\:!vv-1\\5< v*\\<+ # BELONG\r\n v <>: >| >\\:|$ # BIG\r\n | -*\"&/\" :+1 p /\"d\"\\+9%\"d\": \\$_\"A\"-0\\: ^$>| >^ # BLOODY\r\n $ >:#<^>1\\^ v \\+1\\< # BOTH\r\n >011p>11g1+21p >11g:\"d\"%9+\\\"d\"/g 21g:\"d\"%9+\\\"d\"/g - #v_ 11g:9%82**\"r\"+\\9/10p0\\>:1+\\10gg84*-#^_v # BRIDGE\r\n>\"&/\"*-| |!`*\"&/\"p12:+1g12 < < >\\*v >55+\\1-v >\\*v >55+\\1-v $ # BURN\r\n^ p11:+1p/\"d\"\\+9%\"d\":\\\"#\":g11< |:\\< |:< < |:\\< |:< < # CAMPAIGN\r\n 9 v p02:p010-1 \\ -1$< ^$< ^ \\0 \\ $< ^$< ^ \\0-1p13::< ...\r\n g vp01g03_v#-g01:_v#- < ...\r\n . >:30p:20 g\\/+2/: 30g^ vp01g03_v#-g01:_v#- < ...\r\n @ > >$30g1+12p 010p:20p>:30p:20 g\\/+2/: 30g^\r\n ^ < > >$30gv\r\n vp\\\"n\"\\\"|\":<+*297:1-\\ | >:1-\\ | > 13g1+:13p ^\r\n v-\"A\"g/9\\+g41+\"r\"**28%9:g11 : >| >\\:| >v >v\r\n >24p 31g1-14g- 0\\: ^>$:| > $23g\\/55+%34p \"n\"24gg:\"|\"-|>34g-|> 534gg:\"|\"-|>24g-|\r\n >1\\^ >$ v >$ v\r\n v p410p510< vpg42\"n\"g43< vpg435+\"A\"g42<\r\n >v > ^ > ^\r\n >21g:9%82**\"r\"+14g+\\9/g\"A\"-24p\"n\"24gg\"|\"-!|> >> ^\r\n >\"n\"24gg14g+!|\r\n |-g13p41:+1g41 p51+gg42\"n\"*+55g51<\r\n > ^\r\n >15g23g` 15g19g` * !| > 15g19p v\r\n 1 > >$30gv> | > ^\r\n 5 vp01g03_^#-g01:_^#- <: > ^\r\n g >:30p:20 g\\/+2/: 30g^*\r\n > >#^ #p #0 2 #<$ v\r\n > :88*%\"9\"`#^_:88+%:9`#v_:2-#v_v 2\r\n > > > > # >$>$0^\r\n |!-8_^#-7:_^#-6:_^#-5:_^# -3:< g\r\n > ^< 0 <^:p010 <^<-!\r\n >:55+%:7-!#^_:3-!#^_2-!#^_:3%2-#^_^>^", "With this problem I tried a little bit differen methology with designing the problem.\r\nPrograms with massive (16k) input are always kind of ugly in befunge because \r\nall of the data must be in the program code, so I thought I can at least try a little bit around.\r\n\r\nIn this program I seperated the code, as much as I could, into independent subprograms.\r\nAll subprograms can use the [1,0]-[9,0] fields as temporary values, get their input \r\nfrom the stack and write their output also to the stack.\r\nThen I combined them together to build the whole program.\r\n\r\nAll the subprograms are in my [BefungePrograms git repo](https://gogs.mikescher.com/gitmirror/BefungePrograms)\r\n\r\nThis resulted in more readable code and (hopefully) snippets that I can reuse in other programs.\r\nBut the code doesn\'t compress as good (which nobody cares about in this problem, cause of the giant input size)\r\nand I\'m sure I could optimize it a lot by using more global state and shared variables etc.\r\n\r\nI think for my next programs I will continue as I did before and sometimes use independent code snippets\r\n(for example for the integer-squareroot function) but for the big main program I will write it all together.\r\n\r\nThe program works like so:\r\n\r\n1. First we calculate a \"palindromic hash value\" for each input word, this is a hash algorithm that \r\n has no collisions as long as there are max five repeated letters in a word and has the same value for \r\n palindroms.\r\n Practically it is a 26-digit number in base-5 where each digit denotes the amount a specific letter occurs in our word.\r\n We can not use a larger number than 5 for our base because then we would overflow our 64bit numbers.\r\n \r\n2. Next we go through our palindromic list and search for palindroms (words with the same hash)\r\n With some clever sorting tricks we could do this in `log2(n)`, but I will leave this as an \r\n exercise for ther reader and and implement in naively in `n^2`\r\n\r\n3. For each word we iterate through all the squares with the correct digit count.\r\n This means we start with `j`, where `j = 10^(len - 1)` and wnd with `k`, where `k = (10^len) - 1`\r\n \r\n4. Now (for each square) we can generate the numeric value for word B with word A + square as our map.\r\n When we generate our char->digit map (as an 26 element array) we also generate a digit->char map \r\n to test if any digit is mapped to multiple different characters (a failure criteria)\r\n \r\n5. Now we have square A and (possible) square B, with our optimized is-integer-squareroot function from problem 086 \r\n we test if B is a square number. And if this is the case (and B is bigger than our current candidate) we set B\r\n as our current result candidate\r\n \r\n6. After we have done this for all pairs we can return (= print out) our current best candidate.\r\n\r\n\r\nUsed sub programs:\r\n - fixed_base_pow.b93\r\n - read_single_word.b93\r\n - get_palindromic_hash.b93\r\n - integer-squareroot-2.b93\r\n - is-squarenumber.b93\r\n - length_single_word.b93", 1, 145592567, 22714, 258, 199, 18769);
+ Do(99, "Largest exponential", "Comparing two numbers written in index form like 2^11 and 3^7 is not difficult, \r\nas any calculator would confirm that 2^11 = 2048 < 3^7 = 2187.\r\n\r\nHowever, confirming that 632382^518061 > 519432^525806 would be much more difficult, \r\nas both numbers contain over three million digits.\r\n\r\nUsing [base_exp.txt](https://projecteuler.net/project/resources/p099_base_exp.txt), \r\na 22K text file containing one thousand lines with a base/exponent pair on each line, \r\ndetermine which line number has the greatest numerical value.\r\n\r\nNOTE: The first two lines in the file represent the numbers in the example given above.", "v$$$$$$ 519432,525806\r\n XX 00v $< 632382,518061\r\n v 0:5 1p vv <1 466580,530130\r\n v $ $ ## > 0\"2\">:11gg:48*-0`!#^_:\",\"- | 525895,525320\r\n^p110p16< ^ # +1\\0$< 15991,714883\r\n vp04+g04 < vp06< + 960290,502358\r\n : #>1-#v\\#/ #2<^ <: 1 760018,511029\r\n !v<| :\\<***\"@}}\"g01<>$ ^ g 166800,575487\r\nv_ 20p10p01>:2*10g`| |>1^ 210884,564478\r\n$ >$30p0:4v^\\+1\\*2 v p05p0< >>$40#+v 681146,515199\r\n1 0#>030g\"}}@\"**`!|^ $< *g 563395,522587\r\ng g|!`g03***\"@}}\"21+30g:*\"}}@\"**/30^ $00 923525,503780\r\n@ >50p30g2/30p20g50g>:!|6g 595148,520429\r\n > #2/#\\\\#-^#1<^< 177108,572629\r\n 750923,511482\r\n 440902,532446\r\n 881418,505504\r\n ...\r\n ...", "For every number we normalize the Exponentiation to base 2.\r\n(We search the equivalent Power `2^x`).\r\nAnd then we only compare the exponents with each other, practically this\r\nmeans we compare the length of the number in binary representation.\r\n\r\nWe chose 2 as our base because this way we don\'t have to worry too much about \r\nthe precision of our calculations (befunge has no native floating point values).\r\nIf we would have found two entries with the same (overall highest) exponent, we would \r\nhave to calculate the exponent to a higher precision, but fortunately this did not happen.\r\n\r\nFrom `b^e` we can get the normalized fraction `2^(e * log2(b))`.\r\nBut because befunge has no log2 operator we have to go through the dirty work of manually approximating log2.\r\n\r\nWe use [this][1] algorithm to calculate log2.\r\n\r\nFirst we calculate the integer part by simple searching the biggest number `2^n` where `2^n < b`\r\n\r\nThen the real part equals `log2(2^(-n) * b)`, because we don\'t want to caclulate with real numbers we \r\ninsert a Precision factor `F` (in this program we used a value of 1 million).\r\n\r\nNow `y = 2^-n * b` and `rp = log2(y)`. We calculate y by dividing b n-times with two.\r\n\r\nOur final result will be `r = n * e + rp * e`. We can already calculate `n*e`, the only missing part is `rp*e`, \r\nwhich we will call `exporp`.\r\n\r\nThen we repeat the following steps until the value of exporp is no longer changing:\r\n\r\n - count the number of times `m` we have to square `y` until `y >= 2` \r\n - `y = y^(2^m) / 2`\r\n - add `m` to `msum`, the collective sum of all calculated `m` values until now\r\n - divide `e` `msum`-times by two and add the result to `exporp`\r\n\r\nNow we have calculated `exporp`, our result is `r = n * e + exporp`.\r\n\r\nWith this method we can calculate the exponent of our normalized exponentiation.\r\nNext we simply iterate through the whole inpt and search the line number with the greatest base2-exponent.\r\n\r\n[1]: https://en.wikipedia.org/wiki/Binary_logarithm#Iterative_approximation", 1, 5072021, 1107, 63, 1000, 709);
+ Do(100, "Arranged probability", "If a box contains twenty-one coloured discs, composed of fifteen blue discs and six red discs, \r\nand two discs were taken at random, it can be seen that the probability of taking two blue discs, \r\n`P(BB) = (15/21)x(14/20) = 1/2`.\r\n\r\nThe next such arrangement, for which there is exactly 50% chance of taking two blue discs at random, \r\nis a box containing eighty-five blue discs and thirty-five red discs.\r\n\r\nBy finding the first arrangement to contain over `10^12 = 1,000,000,000,000` discs in total, \r\ndetermine the number of blue discs that the box would contain.", "10v>012p >01g11g:01g3*\\4*+01p3*\\2*+11p02g12g:02g3*\\4*-0v\r\n##1^p110<|!`*:**\"@}}\"/4-g20-*g212-g10+*2g112p21-*2\\*3p2<\r\n##>p102p^>402g2*+12g2*+01g2*+11g2*-8/.@", "Let\'s say `b` is the number of blue disks, `r` the number of red disks \r\nand `n` is the total number.\r\nFrom the problem description we can infer this:\r\n~~~\r\nb+r = n (1)\r\n0 < b < n (2)\r\n0 < r < n (3)\r\nn > 10^12 (4)\r\n(b/n)*((b-1)/(n-1)) = 1/2 (5)\r\n~~~\r\n\r\nNow we can user (1) and (2) to get a formula for `b` and `n`:\r\n\r\n~~~\r\n(b/n)*((b-1)/(n-1)) = 1/2\r\n2*b*(b-1) = n * (n-1)\r\n2*b^2 - 2*b = n^2 - n\r\n2 * (b^2 - b) = n^2-n\r\n0.5 * (2b)^2 - (2b) = (n)^2 - (n)\r\n2*(b^2) - 2b = (n)^2 - (n)\r\n\r\nb = 1/2 ( sqrt(2n^2 - 2n + 1) + 1 )\r\n~~~\r\n\r\nFor the last formula we search for integer solutions.\r\nWe can now either solve this manually with diophantine equations,\r\nor we ask [Wolfram|Alpha](www.wolframalpha.com/input/?i=2*b*b-2b+%3D+n*n-n).\r\nWhich gives us the following two formulas:\r\n\r\n~~~\r\ns = sqrt(2)\r\n\r\nb = (1/8) * ( 2*(3-2*s)^m + s*(3-2*s)^m + 2*(3+2*s)^m - s*(3+2*s)^m + 4)\r\nn = (1/4) * ( -(3-2*s)^m - s*(3-2*s)^m - (3+2*s)^m + s*(3+2*s)^m + 2)\r\n\r\nm element Z, m >= 0\r\n~~~\r\n\r\nWe can see both formulas contain the expression sqrt(2), which is not \r\nonly fractional but also irrational. Which is a problem with the strict integer\r\noperations in befunge.\r\n\r\nBut we can sidestep this by using a special number notation `r * 1 + s * sqrt(2)`.\r\nIn every step we calculate the \"real\" part of the number plus a multiple of `sqrt(2)`.\r\nThis is kinda like the common notation of [imaginary numbers](https://en.wikipedia.org/wiki/Imaginary_number).\r\n\r\nNow all we have to do is create algorithms for addition and multiplication in our new number format.\r\n\r\n~~~\r\n(r1 + s1 * sqrt(2)) + (r2 + s2 * sqrt(2)) = (r1+r2) + (s1+s2) * sqrt(2)\r\n(r1 + s1 * sqrt(2)) * (r2 + s2 * sqrt(2)) = (r1*r2+2*s1*s2) + (s1*r2+r1*s2) * sqrt(2)\r\n~~~\r\n\r\nNow we can use the formulas from Wolfram|Alpha until we find a value for `n > 10^12`.\r\n\r\nIn the end this problem wasn\'t that hard to code when all the preparations were done.\r\nAlso it\'s pretty fast.", 0, 1649, 0, 56, 3, 756872327473);
+}
+
+void Do(int Problemnumber, string Problemtitle, string Problemdescription, string Code, string Explanation, int AbbreviatedCode, long SolutionSteps, long SolutionTime, int SolutionWidth, int SolutionHeight, long SolutionValue)
+{
+ StringBuilder b = new StringBuilder();
+
+ b.AppendLine($" {Problemnumber},");
+ b.AppendLine($"\t'title' => '{ToLiteral(Problemtitle)}',");
+ b.AppendLine($"\t'description' => function(){{ return file_get_contents(__DIR__ . '/euler_{Problemnumber:000}_description.md'); }},");
+ b.AppendLine($"\t'code' => function(){{ return file_get_contents(__DIR__ . '/euler_{Problemnumber:000}_code.txt'); }},");
+ b.AppendLine($"\t'explanation' => function(){{ return file_get_contents(__DIR__ . '/euler_{Problemnumber:000}_explanation.md'); }},");
+ b.AppendLine($"\t'url_euler' => 'http://projecteuler.net/problem={Problemnumber:000}',");
+ b.AppendLine($"\t'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-{Problemnumber:000}.b93',");
+ b.AppendLine($"\t'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',");
+ b.AppendLine($"\t'abbreviated' => {(AbbreviatedCode != 0).ToString().ToLower()},");
+ b.AppendLine($"\t'steps' => {SolutionSteps},");
+ b.AppendLine($"\t'time' => {SolutionTime},");
+ b.AppendLine($"\t'width' => {SolutionWidth},");
+ b.AppendLine($"\t'height' => {SolutionHeight},");
+ b.AppendLine($"\t'value' => {SolutionValue},");
+ b.AppendLine($"];");
+
+ File.WriteAllText(@"C:\Users\schwoerm\Desktop\M\hp\v4\www\rawdata\euler\" + $"euler_{Problemnumber:000}.php", b.ToString(), ENC);
+ File.WriteAllText(@"C:\Users\schwoerm\Desktop\M\hp\v4\www\rawdata\euler\" + $"euler_{Problemnumber:000}_description.md", Problemdescription, ENC);
+ File.WriteAllText(@"C:\Users\schwoerm\Desktop\M\hp\v4\www\rawdata\euler\" + $"euler_{Problemnumber:000}_code.txt", Code, ENC);
+ File.WriteAllText(@"C:\Users\schwoerm\Desktop\M\hp\v4\www\rawdata\euler\" + $"euler_{Problemnumber:000}_explanation.md", Explanation, ENC);
+
+}
+
+private static string ToLiteral(string input)
+{
+ using (var writer = new StringWriter())
+ {
+ using (var provider = CodeDomProvider.CreateProvider("CSharp"))
+ {
+ provider.GenerateCodeFromExpression(new CodePrimitiveExpression(input), writer, null);
+ var a = writer.ToString();
+ return a.Substring(1, a.Length - 2);
+ }
+ }
+}
\ No newline at end of file
diff --git a/data/ConvertFromDB_Programs.linq b/data/ConvertFromDB_Programs.linq
new file mode 100644
index 0000000..a7b3bf9
--- /dev/null
+++ b/data/ConvertFromDB_Programs.linq
@@ -0,0 +1,93 @@
+
+ System.CodeDom.Compiler
+ System.CodeDom
+
+
+Encoding ENC = new UTF8Encoding(false);
+
+void Main()
+{
+ Do(1, "All in One", "All in One", 1439, "Tool", 1, 1, 1, "German", "Delphi", "A little \"swiss army knife\" programm with over 100 different functionalities", "2008-11-26", "direkt", "", "", "", 0, "", -1);
+ Do(2, "Beepster", "Beepster", 1960, "Hoax", 0, 1, 1, "English", "Delphi", "Annoy your teachers/freinds with a very high pitched sound, even without external speakers.", "2008-06-04", "direkt", "", "", "", 0, "", -1);
+ Do(3, "Blitzer", "Blitzer", 1869, "Hoax", 0, 1, 1, "English", "Delphi", "Hoax you teachers/friends with flashing lights on your monitor.", "2008-05-05", "direkt", "", "", "", 0, "", -1);
+ Do(4, "Deal or no Deal", "Deal or no Deal", 1279, "Game", 0, 1, 1, "German", "Delphi", "A digital version of the same-named german tv-show game.", "2008-10-08", "direkt", "", "", "", 0, "", -1);
+ Do(5, "exeExtract", "exe Extract", 1818, "Tool", 0, 1, 1, "English", "Delphi", "A simple tool to copy all files of a specific extension from a folder.", "2008-03-26", "direkt", "", "", "", 0, "", -1);
+ Do(6, "Graveyard of Numbers", "G. o. N.", 1221, "Tool", 0, 1, 1, "German", "Delphi", "A little tool to continuously rename files.", "2008-10-01", "direkt", "", "", "", 0, "", -1);
+ Do(7, "LightShow", "LightShow", 1888, "Hoax", 0, 1, 1, "German", "Delphi", "Turn you keyboard-LED\"s into a little lightshow", "2008-10-12", "direkt", "", "", "", 0, "", -1);
+ //Do(8, "Penner-Bot", "Penner Bot", 3722, "Bot", 0, 0, 0, "German", "C++", "Cheat in the browsergame \"Pennergame\" and get a lot of Bottles free.", "2008-10-22", "direkt", "", "", "", 0, "", -1);
+ Do(9, "Ziegenproblem", "Ziegenproblem", 2257, "Mathematics", 0, 1, 1, "German", "Delphi", "Simulate the popular Monty Hall problem (ger: Ziegenproblem) with this program for yourself.", "2008-04-10", "direkt", "", "", "", 0, "", -1);
+ //Do(10, "Niripsa", "Niripsa", 1604, "Game", 1, 1, 0, "German", "Delphi", "A clone of the game \"Aspirin\" in space.", "2008-11-19", "direkt", "", "", "", 0, "", -1);
+ Do(11, "NedSchend", "Nedschend", 1563, "Hoax", 1, 1, 1, "German", "Delphi", "Send anonymous messages over the Windows Messenger service to other pc\"s in your LAN", "2009-02-11", "direkt", "", "", "", 0, "", -1);
+ Do(12, "Sieb des Eratosthenes", "Sieb des E.", 1671, "Mathematics", 1, 1, 1, "German", "Delphi", "Visualize the prime number calculation with the Sieve of Erastothenes algorithm.", "2009-01-22", "direkt", "", "", "", 0, "", -1);
+ Do(13, "Logistixx", "Logistixx", 1599, "Mathematics", 1, 1, 1, "German", "Delphi", "Find the trick to escape the seemingly escape-proof maze.", "2008-12-20", "direkt", "", "", "", 0, "", -1);
+ Do(14, "H2O", "H²O", 1953, "Game", 2, 1, 1, "English", "Delphi", "Try creating the biggest chain reaction and see yourself climb up in the global leaderboard.", "2009-01-24", "direkt", "", "", "", 0, "H²O", 2);
+ Do(15, "LAN-Control", "LAN-Control", 1781, "Network administration", 1, 1, 1, "German", "Delphi", "Controll essential features of an other computer over the LAN", "2011-07-05", "direkt", "", "", "", 0, "LAN-Control", -1);
+ Do(16, "Smart Directory Lister", "SDL", 1064, "Tool", 2, 1, 1, "German", "Delphi", "List all files in a folder that match a specific pattern and export them in plaintext.", "2010-01-12", "direkt", "", "", "", 0, "", -1);
+ //Do(17, "Wikipedia - The Game", "Wiki Game", 318, "Game", 1, 1, 0, "German", "Delphi", "Expand your knowledge while you read trough wikipedia articles to find the way to your target.", "2010-05-29", "direkt", "", "", "", 0, "WTG", 3);
+ //Do(18, "ClipCorn", "ClipCorn", 126, "Tool", 3, 0, 0, "German", "Delphi", "Collect and Organize all your movies central and portable in a database.", "2010-06-26", "direkt", "", "", "", 0, "ClipCorn", -1);
+ Do(19, "Dynamic Link Fighters", "DLF", 1296, "Game", 1, 1, 1, "English|German", "Delphi", "Program your own KI and let it fight against others in a brutal deathmatch.", "2010-12-04", "direkt", "", "", "", 0, "DLF", -1);
+ Do(20, "TicTacToe", "Tic Tac Toe", 1422, "Game", 1, 1, 1, "English", "Delphi", "The classical Tic-Tac-Toe, complete with perfect KI and Sourcecode.", "2011-01-19", "direkt", "", "", "", 0, "", -1);
+ Do(21, "Keygen Dancer", "Keygen Dancer", 665, "Gadget", 2, 1, 1, "English", "Delphi", "40 of the best keygen themes together with a funny little keygen dance animation.", "2010-03-16", "", "", "", "", 0, "", -1);
+ Do(22, "Infinity Tournament", "Inf. Tournament", 1258, "Game", 4, 1, 1, "English", "Java", "A never ending Tower Defense where you fight against your own score.", "2012-04-14", "direkt", "", "", "", 1, "InfinityTournament", 4);
+ Do(23, "jCircuits", "jCircuits", 1411, "Simulation", 4, 1, 1, "English", "Java", "A fully featured logical circuit simulator with many prebuild components", "2011-12-16", "direkt", "http://sourceforge.net/projects/jcircuits/", "", "", 0, "", -1);
+ Do(24, "Borderline Defense", "Borderline Defense", 1042, "Game", 4, 1, 1, "English", "Java", "A improved Space-Invaders clone - programmed from the Java-AG, Oken.", "2012-05-24", "direkt", "", "http://borderlinedefense.99k.org/", "", 1, "", 5);
+ Do(25, "absCanvas", "absCanvas", 1442, "Engine", 3, 1, 1, "English", "Java", "A powerful 2D Tiled-Game-Engine for java. Completely in canvas and with network support.", "2012-05-28", "direkt", "", "", "", 0, "absCanvas", -1);
+ Do(26, "Crystal Grid", "Crystal Grid", 1032, "Game", 4, 1, 1, "English", "Java", "A challenging, tactical mini-game in blueprint-style.", "2013-01-03", "direkt", "", "", "", 1, "CrystalGrid", 6);
+ Do(28, "jClipCorn", "jClipCorn", 432, "Tool", 4, 1, 1, "English|German", "Java", "Organize your movies and series on an external hard drive.", "2012-10-28", "https://github.com/Mikescher/jClipCorn/releases", "", "", "https://github.com/Mikescher/jClipCorn/wiki", 0, "jClipCorn", -1);
+ Do(29, "BefunZ", "BefunZ", 1005, "Interpreter", 3, 1, 1, "English", "C#", "A Befunge-93 Interpreter compatible with Befunge-98 dimensions.", "2013-05-03", "direkt", "", "", "", 0, "", -1);
+ Do(30, "Serpilicum", "Serpilicum", 846, "Game", 3, 1, 1, "English", "C++", "A crazy little Snake with an \"Console\" Style", "2013-07-08", "direkt", "", "", "https://github.com/Mikescher/Serpilicum", 0, "", -1);
+ Do(32, "SuperBitBros", "SuperBitBros", 870, "Game", 4, 1, 1, "English", "C#", "A clone of all original SuperMarioBros (NES) levels, with a few tweaks.", "2013-10-17", "direkt", "", "", "https://github.com/Mikescher/SuperBitBros", 0, "", -1);
+ Do(35, "ExtendedGitGraph", "ExtendedGitGraph", 514, "Library", 2, 1, 1, "English", "PHP", "A simple php module to display a overview of you github commits", "2014-06-08", "https://github.com/Mikescher/extendedGitGraph/", "", "", "", 0, "", -1);
+ Do(36, "SharkSim", "SharkSim", 428, "Simulation", 3, 1, 1, "English", "C++", "A simple implementation of the Wa-Tor cellular automaton", "2013-07-12", "", "", "", "", 0, "", -1);
+ Do(37, "jQCCounter", "jQCCounter", 457, "Tool", 3, 1, 1, "English", "Java", "A little tool to find the \"line of codes\" of multiple projects", "2014-04-27", "", "", "", "https://github.com/Mikescher/jQCCounter", 0, "", -1);
+ Do(38, "BefunUtils", "BefunUtils", 764, "Compiler", 4, 1, 1, "English", "C#", "My selfmade Code-to-Befunge93 compiler, with a few little extras.", "2014-08-04", "", "", "", "https://github.com/Mikescher/BefunUtils", 0, "", -1);
+ Do(39, "HexSolver", "HexSolver", 423, "Tool", 5, 1, 1, "English", "C#", "An automatic parser and solver for Hexcells, Hexcells Plus and Hexcells Infinite.", "2015-05-06", "", "", "", "https://github.com/Mikescher/HexSolver", 0, "", -1);
+ Do(40, "Passpad", "Passpad", 363, "Tool", 3, 1, 1, "English", "C#", "A texteditor for encrypted textfiles (AES, Twofish, Blowfish, ...)", "2015-11-26", "https://github.com/Mikescher/Passpad/releases", "", "", "https://github.com/Mikescher/Passpad", 0, "", -1);
+
+}
+
+void Do(int ID, string Name, string Thumbnailname, int Downloads, string Kategorie, int Sterne, int enabled, int visible,
+ string Language, string programming_lang, string Description, string add_date,
+ string download_url, string sourceforge_url, string homepage_url, string github_url,
+ int uses_absCanv, string update_identifier, int highscore_gid)
+{
+ StringBuilder b = new StringBuilder();
+
+ b.AppendLine($" '{Name}',");
+ b.AppendLine($"\t'category' => '{Kategorie}',");
+ b.AppendLine($"\t'stars' => {Sterne},");
+ b.AppendLine($"\t'ui_language' => '{Language}',");
+ b.AppendLine($"\t'prog_language' => '{programming_lang}',");
+ b.AppendLine($"\t'short_description' => '{ToLiteral(Description)}',");
+ b.AppendLine($"\t'add_date' => '{add_date}',");
+ b.AppendLine($"\t'urls' =>");
+ b.AppendLine($"\t[");
+ if (!string.IsNullOrWhiteSpace(download_url)) b.AppendLine($"\t\t'download' => '{ToLiteral(download_url)}',");
+ if (!string.IsNullOrWhiteSpace(sourceforge_url)) b.AppendLine($"\t\t'sourceforge' => '{ToLiteral(sourceforge_url)}',");
+ if (!string.IsNullOrWhiteSpace(homepage_url)) b.AppendLine($"\t\t'homepage' => '{ToLiteral(homepage_url)}',");
+ if (!string.IsNullOrWhiteSpace(github_url)) b.AppendLine($"\t\t'github' => '{ToLiteral(github_url)}',");
+ b.AppendLine($"\t],");
+ b.AppendLine($"\t'long_description' => function(){{ return file_get_contents(__DIR__ . '/{Name}_description.md'); }},");
+ b.AppendLine($"\t'thumbnail_url' => '/images/program_thumbnails/{Name}.png',");
+ b.AppendLine($"];");
+
+ File.WriteAllText(@"C:\Users\schwoerm\Desktop\M\hp\v4\www\rawdata\programs\" + $"{Name}.php", b.ToString(), ENC);
+ File.WriteAllText(@"C:\Users\schwoerm\Desktop\M\hp\v4\www\rawdata\programs\" + $"{Name}_description.md", File.ReadAllText(@"C:\Users\schwoerm\Desktop\M\hp\v3\www\data\programs\desc\" + Name + @"\index.markdown"), ENC);
+}
+
+private static string ToLiteral(string input)
+{
+ using (var writer = new StringWriter())
+ {
+ using (var provider = CodeDomProvider.CreateProvider("CSharp"))
+ {
+ provider.GenerateCodeFromExpression(new CodePrimitiveExpression(input), writer, null);
+ var a = writer.ToString();
+ return a.Substring(1, a.Length-2);
+ }
+ }
+}
\ No newline at end of file
diff --git a/www/data/styles.css b/www/data/styles.css
index 56c19b7..76bd65c 100644
--- a/www/data/styles.css
+++ b/www/data/styles.css
@@ -126,15 +126,23 @@ body {
display: flex;
align-items: center;
justify-content: center;
-
- color: #222;
- font-weight: bold;
+
padding: 4px;
background: #AAA;
-
+}
+
+.euler_pnl_header a {
+ color: #222;
+ font-weight: bold;
+ text-decoration: none;
+
font-size: large;
}
+.euler_pnl_header a:hover {
+ text-decoration: underline;
+}
+
.euler_pnl_content {
display: flex;
flex-direction: column;
@@ -171,9 +179,18 @@ body {
justify-content: center;
}
+.euler_pnl_cell:hover {
+ box-shadow: 0 0 4px #000000;
+}
+
.euler_pnl_cell a {
color: black;
text-decoration: none;
+ width: 100%;
+ height: 100%;
+ display: flex;
+ justify-content: center;
+ align-items: center;
}
.euler_pnl_cell a:hover {
diff --git a/www/fragments/blog/borderlinedef.md b/www/fragments/blog/borderlinedef.md
new file mode 100644
index 0000000..a878ac1
--- /dev/null
+++ b/www/fragments/blog/borderlinedef.md
@@ -0,0 +1,13 @@
+Perhaps I'm making too much Mini-Games, but hey .... here is another one:
+
+I proudly present you [Borderline Defense](/programs/view/Borderline%20Defense). Borderline Defense is a funny little Space-Invaders-Clone and the final project of 2 years Delphi-AG.
+Programmed (and designed) from the members of the Delphi-AG and the two leaders (Benjamin and myself) has it grown into a playable and quite funny game.
+The background work is done by my [absCanvas](/programs/view/AbsCanvas)-Engine and the Special features are:
+
+ - Endless Gameplay (as long as you can last)
+ - An Online-Highscore
+ - A Boss Fight at stage 20 (and 40, 60, 80 etc )
+ - And a ship with 10 different upgrade levels
+
+So, thats it ... have fun
+Mike
\ No newline at end of file
diff --git a/www/fragments/blog/bsod.md b/www/fragments/blog/bsod.md
new file mode 100644
index 0000000..6319273
--- /dev/null
+++ b/www/fragments/blog/bsod.md
@@ -0,0 +1,10 @@
+Some people say flying gets safer and safer ... But see for your self:
+
+![Bluescreen_01][1]
+
+![Bluescreen_02][2]
+
+I think I will use the train :D
+
+ [1]: /images/log/bsod_1.jpg
+ [2]: /images/log/bsod_2.jpg
\ No newline at end of file
diff --git a/www/fragments/blog/cleanup.md b/www/fragments/blog/cleanup.md
new file mode 100644
index 0000000..aba6109
--- /dev/null
+++ b/www/fragments/blog/cleanup.md
@@ -0,0 +1,21 @@
+Yesterday I decided that a lot of my website is out of date and I should probably re-evaluate whats on here.
+To be short: I completely removed the fun-page, most links were netherless broken and the rest didn't really fit this page.
+Also I re-did the Downlaodpage, you can now see
+
+ - absCanvas-Links
+ - Versionnumbers
+ - The sourcecode from a few programs
+ - Sort by Date
+ - The last added program on the mainpage
+
+and a lot more.
+
+Also I improved my Adminpage, hopefully I can now more easily upload and change programs/logs.
+
+Finally I have an PSA for you: While writing my PHP-Code i found a pretty cool Editor (previously I used Notepad++):
+[Weaverslave 4](http://www.weaverslave.ws/)
+
+
+You all a good day
+~ Mike
+
diff --git a/www/fragments/blog/crystalgrid.md b/www/fragments/blog/crystalgrid.md
new file mode 100644
index 0000000..fea83fc
--- /dev/null
+++ b/www/fragments/blog/crystalgrid.md
@@ -0,0 +1,8 @@
+The same procedure as last program ?
+The same procedureas **every** program.
+
+You see nothing really different, i wrote a little game in my spare free time. And now I'm uploading it.
+It's a little game named [Crystal Grid](/programs/view/Crystal%20Grid). Im pretty proud of the difficulty. It's pretty forgiving as long as you play on `Beginner` but extremely challenging on `Impossible`.
+
+If you dare (and like) you can try beat my highscore
+... Mike
diff --git a/www/fragments/blog/funupdate.md b/www/fragments/blog/funupdate.md
new file mode 100644
index 0000000..8a6a2e0
--- /dev/null
+++ b/www/fragments/blog/funupdate.md
@@ -0,0 +1,6 @@
+After a lot of requests i come to update the [Fun-Page](/fun/fun.php).
+The flying parts are now a good amount slower and the colors not *that* bright ...
+
+Complaints can go into the guestbook.
+
+Greetings Mike
\ No newline at end of file
diff --git a/www/fragments/blog/hack.md b/www/fragments/blog/hack.md
new file mode 100644
index 0000000..1c0fab8
--- /dev/null
+++ b/www/fragments/blog/hack.md
@@ -0,0 +1,14 @@
+I have to say: "Wow" .
+
+Someone really took the time to *"hack"* my website.
+Yesterday someone changed my files to display this messsage on the mainpage:
+
+>
+> **Diese Seite wurde gehackt.**
+> Sorry wegen der Shoutbox, die ist
+> jetzt e bissle verschoben :D
+> *Und sie bleibt es auch, bis die Sicherheitslücke entfernt ist :P*
+>
+
+I think if found the hole, and *hopefully* i prevented all future XSS-atacks
+I hope there will be no more ... suprises.
\ No newline at end of file
diff --git a/www/fragments/blog/inftournament.md b/www/fragments/blog/inftournament.md
new file mode 100644
index 0000000..e3da207
--- /dev/null
+++ b/www/fragments/blog/inftournament.md
@@ -0,0 +1,8 @@
+Okay, okay, after a loooong time I will write something in the log.
+In the last few months there wasn't much on this site, but be sure mikescher.de is not *(yet)* dead.
+I just have a lot to do with my abi and beside that I'm working on our Clan-homepage [SemteX](http://www.semtex.org).
+
+But I also wrote a few programs and I want to upload one which has gotten quite a bit of progress and is nearly finished: [Infinity Tournament](/programs/view/Infinity%20Tournament) 1.2.
+It's based on an old game by me, but writte completely frokm scratch new in my on 2D-Canvas Engine ([absCanvas](/programs/view/AbsCanvas)) ... have fun
+
+*Mikescher*
\ No newline at end of file
diff --git a/www/fragments/blog/initial.md b/www/fragments/blog/initial.md
new file mode 100644
index 0000000..e0b73a9
--- /dev/null
+++ b/www/fragments/blog/initial.md
@@ -0,0 +1,15 @@
+After a kinda long wait the new Style is finally online. You can now look at the glorious *mikescher.de 3.0*
+
+Write in the (also new) Guestbook what you think about it.
+Here is a little overview over the past versions:
+
+
+**v1.0:** ![version 1][1]
+
+**v2.0:** ![version 2][2]
+
+**v3.0:** ![version 3][3]
+
+ [1]: /images/log/ms_de_v1.jpg
+ [2]: /images/log/ms_de_v2.jpg
+ [3]: /images/log/ms_de_v3.jpg
\ No newline at end of file
diff --git a/www/fragments/blog/lancontrol.md b/www/fragments/blog/lancontrol.md
new file mode 100644
index 0000000..71f4ea8
--- /dev/null
+++ b/www/fragments/blog/lancontrol.md
@@ -0,0 +1,8 @@
+I have uploaded another of my older programs: [LAN-Control 2.0](/programs/view/LAN-Control).
+You probably didn't even know the 1.0 version, because i never came to publish that version either.
+And, to be quite frankly, it wasn't really a thing i would show others.
+
+But now the completely rewrote version is online and if you want you can test it out.
+
+
+MfG Mike
\ No newline at end of file
diff --git a/www/fragments/blog/language.txt b/www/fragments/blog/language.txt
new file mode 100644
index 0000000..d20264f
--- /dev/null
+++ b/www/fragments/blog/language.txt
@@ -0,0 +1,6 @@
+Hi,
+
+I am currently changing the main languages of this website to *english*.
+That means not only that all future Logs will be written in english, but also that i will translate the old ones.
+
+Enjoy.
\ No newline at end of file
diff --git a/www/fragments/blog/more_euler.md b/www/fragments/blog/more_euler.md
new file mode 100644
index 0000000..a09f336
--- /dev/null
+++ b/www/fragments/blog/more_euler.md
@@ -0,0 +1,8 @@
+A lot of you probably have seen [various](/programs/view/BefunUtils) [befunge](/programs/view/BefunZ) [stuff](https://github.com/Mikescher/BefunUtils) on this site.
+
+But a thing I do now for a while is solving the **[Project Euler](https://projecteuler.net/)** problems in befunge.
+To celebrate fifty solved levels I want to rally you again to my **[blogpost about this project](/blog/1/Project_Euler_with_Befunge)** and the [table](/blog/1/Project_Euler_with_Befunge) with all my solved problems.
+
+Have a look and perhaps feel inspired to do a few problems by your self - most of them are quite fun and challenging.
+
+
\ No newline at end of file
diff --git a/www/fragments/blog/newlayout.txt b/www/fragments/blog/newlayout.txt
new file mode 100644
index 0000000..f4a82cb
--- /dev/null
+++ b/www/fragments/blog/newlayout.txt
@@ -0,0 +1,6 @@
+I can proudly say, i finally started the new *(and better)* Layout.
+Simultaneously i have started this log.
+
+I hope many more log-entries will follow.
+
+~ Mike
\ No newline at end of file
diff --git a/www/fragments/blog/spammers.md b/www/fragments/blog/spammers.md
new file mode 100644
index 0000000..744ee02
--- /dev/null
+++ b/www/fragments/blog/spammers.md
@@ -0,0 +1,9 @@
+*grml* After you guys started spamming my guestbook I saw myself forced towards a little bit of more drastic measures.
+So you are now forced to solve a capture everytime you want to post something.
+Have fun :)
+
+Btw, i took the "fun" path and tried writing my own captcha code, here you can see the result:
+
+![Captcha][1]
+
+ [1]: /images/log/captcha_img.png
\ No newline at end of file
diff --git a/www/fragments/blog/v4.md b/www/fragments/blog/v4.md
new file mode 100644
index 0000000..ef75fc9
--- /dev/null
+++ b/www/fragments/blog/v4.md
@@ -0,0 +1,16 @@
+When you see this Log you probably notice that this site looks a whole lot different than a few days before.
+And you you can probably guess it **I rewrote this website completely from scratch**.
+Finally there is a *real* PHP Framework behind this all ([Yii](http://www.yiiframework.com/) with [Yiistrap](http://www.getyiistrap.com/)) and my code looks kinda good and is [version controlled](https://github.com/Mikescher/www.mikescher.de).
+
+My hopes are that I can now easier add new programs and that the whole page looks a bit more professional.
+If you want to see how this page has evolved over the years - here are the thumbnails of mikescher.de version `1`, `2`, `3` and the current `4`:
+
+
+
+
+
+
+Also look at the new [Blog section](/blog), for now there is not much content but perhaps that will change over te next few months.
+
+Greetings
+~ Mikescher
\ No newline at end of file
diff --git a/www/fragments/euler.php b/www/fragments/euler.php
deleted file mode 100644
index d366ca4..0000000
--- a/www/fragments/euler.php
+++ /dev/null
@@ -1,81 +0,0 @@
-
-query('SELECT * FROM ms4_eulerproblem', PDO::FETCH_ASSOC);
-
-?>
-
-
-
-
-
-
- \n";
- echo "
\n";
- for ($i = 1; $i <= $max; $i++)
- {
- $cssclass = '';
- if (key_exists($i, $arr))
- {
- $cssclass = $arr[$i]['timelevel'];
- }
- else
- {
- $cssclass = 'euler_pnl_cell_notexist';
- }
-
- echo "
\n";
-
- if (($i)%20 == 0)
- {
- echo "
\n";
- echo "
\n";
- echo "
\n";
- echo "
\n";
- }
- else if (($i)%10 == 0)
- {
- echo "
\n";
- echo "
\n";
- }
- }
- echo "
\n";
- echo "
\n";
-
-
- ?>
-
+
+
+
+
+ \n";
+ echo "
\n";
+ for ($i = 1; $i <= $max; $i++)
+ {
+ $cssclass = 'euler_pnl_cell_notexist';
+ $alttitle = '';
+ $href = '#';
+ if (key_exists($i, $arr))
+ {
+ $cssclass = $RATING_CLASSES[$arr[$i]['rating']];
+ $alttitle = $arr[$i]['title'];
+ $href = "/blog/1/Project_Euler_with_Befunge/problem-" . str_pad($i, 3, '0', STR_PAD_LEFT);
+ }
+
+ echo "
\n";
+
+ if (($i)%20 == 0)
+ {
+ echo "
\n";
+ echo "
\n";
+ echo "
\n";
+ echo "
\n";
+ }
+ else if (($i)%10 == 0)
+ {
+ echo "
\n";
+ echo "
\n";
+ }
+ }
+ echo "
\n";
+ echo "
\n";
+
+ ?>
+
-
+
diff --git a/www/statics/euler/euler_001.php b/www/statics/euler/euler_001.php
new file mode 100644
index 0000000..5e30d33
--- /dev/null
+++ b/www/statics/euler/euler_001.php
@@ -0,0 +1,19 @@
+ 1,
+ 'title' => 'Multiples of 3 and 5',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_001_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_001_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_001_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=001',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-001.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 47624,
+ 'time' => 62,
+ 'width' => 30,
+ 'height' => 5,
+ 'value' => 233168,
+];
diff --git a/www/statics/euler/euler_001_code.txt b/www/statics/euler/euler_001_code.txt
new file mode 100644
index 0000000..4b0c8a4
--- /dev/null
+++ b/www/statics/euler/euler_001_code.txt
@@ -0,0 +1,5 @@
+vvv: < <
+1> 1+:::3/3*-!#^_>::5/5*-!#^_v
+1$v ># v# ># v#<
+1 >:5558***-!|v$<>+\:1-!|v$<
+>^ <>$$^\ <>.@
\ No newline at end of file
diff --git a/www/statics/euler/euler_001_description.md b/www/statics/euler/euler_001_description.md
new file mode 100644
index 0000000..4c4864c
--- /dev/null
+++ b/www/statics/euler/euler_001_description.md
@@ -0,0 +1,3 @@
+If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23.
+
+Find the sum of all the multiples of 3 or 5 below 1000.
\ No newline at end of file
diff --git a/www/statics/euler/euler_001_explanation.md b/www/statics/euler/euler_001_explanation.md
new file mode 100644
index 0000000..905fb64
--- /dev/null
+++ b/www/statics/euler/euler_001_explanation.md
@@ -0,0 +1 @@
+The solution here is pretty straight-forward, going through all numbers from 1-1000 and adding all multiples of 3 and 5 together.
\ No newline at end of file
diff --git a/www/statics/euler/euler_002.php b/www/statics/euler/euler_002.php
new file mode 100644
index 0000000..c65fb6b
--- /dev/null
+++ b/www/statics/euler/euler_002.php
@@ -0,0 +1,19 @@
+ 2,
+ 'title' => 'Even Fibonacci numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_002_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_002_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_002_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=002',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-002.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 1669,
+ 'time' => 62,
+ 'width' => 26,
+ 'height' => 5,
+ 'value' => 4613732,
+];
diff --git a/www/statics/euler/euler_002_code.txt b/www/statics/euler/euler_002_code.txt
new file mode 100644
index 0000000..3a9439b
--- /dev/null
+++ b/www/statics/euler/euler_002_code.txt
@@ -0,0 +1,5 @@
+v>v>ppp 0>>$ 10g20g:10p+:v
+202 >00p0^|-*2/2::< vp02<
+0::0^+ g00^@$.g00<>*` #v_^
+>^ ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_002_description.md b/www/statics/euler/euler_002_description.md
new file mode 100644
index 0000000..ff8bdcb
--- /dev/null
+++ b/www/statics/euler/euler_002_description.md
@@ -0,0 +1,8 @@
+Each new term in the Fibonacci sequence is generated by adding the previous two terms.
+By starting with 1 and 2, the first 10 terms will be:
+
+~~~
+1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
+~~~
+
+By considering the terms in the Fibonacci sequence whose values do not exceed four million, find the sum of the even-valued terms.
\ No newline at end of file
diff --git a/www/statics/euler/euler_002_explanation.md b/www/statics/euler/euler_002_explanation.md
new file mode 100644
index 0000000..f3f1ebb
--- /dev/null
+++ b/www/statics/euler/euler_002_explanation.md
@@ -0,0 +1 @@
+Also the problem here was not the algorithm, but writing and compressing it in Befunge. The code calculates the Fibonacci sequence one after each other and remembers the sum while iterating.
\ No newline at end of file
diff --git a/www/statics/euler/euler_003.php b/www/statics/euler/euler_003.php
new file mode 100644
index 0000000..ab266f1
--- /dev/null
+++ b/www/statics/euler/euler_003.php
@@ -0,0 +1,19 @@
+ 3,
+ 'title' => 'Largest prime factor',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_003_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_003_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_003_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=003',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-003.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 31579516,
+ 'time' => 9547,
+ 'width' => 55,
+ 'height' => 4,
+ 'value' => 6857,
+];
diff --git a/www/statics/euler/euler_003_code.txt b/www/statics/euler/euler_003_code.txt
new file mode 100644
index 0000000..a0d062c
--- /dev/null
+++ b/www/statics/euler/euler_003_code.txt
@@ -0,0 +1,4 @@
+89197939490919v >00g10g1-:10p%#v_10g:30p1-40pv
+v+*29191929891< ^ < <_v#! %g04g03<
+>*+*+*+*+*+*+*v >"{.i "+**10p#^ #p #0 #0 <>40g:1-40p2-|
+ >#^ +# *# +# *# +# *# +# *# +# <@.g03<
\ No newline at end of file
diff --git a/www/statics/euler/euler_003_description.md b/www/statics/euler/euler_003_description.md
new file mode 100644
index 0000000..b6bed74
--- /dev/null
+++ b/www/statics/euler/euler_003_description.md
@@ -0,0 +1,3 @@
+The prime factors of 13195 are 5, 7, 13 and 29.
+
+What is the largest prime factor of the number 600851475143 ?
\ No newline at end of file
diff --git a/www/statics/euler/euler_003_explanation.md b/www/statics/euler/euler_003_explanation.md
new file mode 100644
index 0000000..28a830e
--- /dev/null
+++ b/www/statics/euler/euler_003_explanation.md
@@ -0,0 +1,3 @@
+This problem is the reason why I changed the internals of my interpreter to int64 (because the numbers are too big for int32).
+
+Fortunately the number is still small enough to brute-force the prime factors, going from the biggest factor to the smallest, the first factor (that is also a prime) that my code finds is the solution.
\ No newline at end of file
diff --git a/www/statics/euler/euler_004.php b/www/statics/euler/euler_004.php
new file mode 100644
index 0000000..65cc4ac
--- /dev/null
+++ b/www/statics/euler/euler_004.php
@@ -0,0 +1,19 @@
+ 4,
+ 'title' => 'Largest palindrome product',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_004_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_004_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_004_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=004',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-004.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 230611114,
+ 'time' => 77813,
+ 'width' => 71,
+ 'height' => 6,
+ 'value' => 906609,
+];
diff --git a/www/statics/euler/euler_004_code.txt b/www/statics/euler/euler_004_code.txt
new file mode 100644
index 0000000..4c65324
--- /dev/null
+++ b/www/statics/euler/euler_004_code.txt
@@ -0,0 +1,6 @@
+1:010:pp5558***04p>10g1+::10p04g-00g \#v_1+:00p\$1:10p\:04g- #v_$$03g.@
+ ^ v $< >1# 0# 1# p# *# :# v# <
+ v_v#-g1-g20g10g 1g2002g1+:02p 01 g - | > ^
+ > ^ >:03g\`#v_03pv
+ ^ $< 0<
\ No newline at end of file
diff --git a/www/statics/euler/euler_004_description.md b/www/statics/euler/euler_004_description.md
new file mode 100644
index 0000000..d78c9dd
--- /dev/null
+++ b/www/statics/euler/euler_004_description.md
@@ -0,0 +1,3 @@
+A palindromic number reads the same both ways. The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.
+
+Find the largest palindrome made from the product of two 3-digit numbers.
\ No newline at end of file
diff --git a/www/statics/euler/euler_004_explanation.md b/www/statics/euler/euler_004_explanation.md
new file mode 100644
index 0000000..b3e02bf
--- /dev/null
+++ b/www/statics/euler/euler_004_explanation.md
@@ -0,0 +1 @@
+Again we can write our program fast enough to brute-force the solution. So we iterate through every possible 3-digit product and check if its a palindrom.
\ No newline at end of file
diff --git a/www/statics/euler/euler_005.php b/www/statics/euler/euler_005.php
new file mode 100644
index 0000000..89e9ad7
--- /dev/null
+++ b/www/statics/euler/euler_005.php
@@ -0,0 +1,19 @@
+ 5,
+ 'title' => 'Smallest multiple',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_005_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_005_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_005_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=005',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-005.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 50166,
+ 'time' => 47,
+ 'width' => 73,
+ 'height' => 6,
+ 'value' => 232792560,
+];
diff --git a/www/statics/euler/euler_005_code.txt b/www/statics/euler/euler_005_code.txt
new file mode 100644
index 0000000..430767c
--- /dev/null
+++ b/www/statics/euler/euler_005_code.txt
@@ -0,0 +1,6 @@
+45*00p110p120p >10g20g*10p00g20g1+:20p`#v_10g.@
+ ^_v#`g00p03+1:g03 10g30g% |1 <^ p01/g03g01<
+ >10g30g/40p150p > 20g50g1+:50p` #v_^
+ ^ < |!%g05g04 <
+ ^<
\ No newline at end of file
diff --git a/www/statics/euler/euler_005_description.md b/www/statics/euler/euler_005_description.md
new file mode 100644
index 0000000..8165258
--- /dev/null
+++ b/www/statics/euler/euler_005_description.md
@@ -0,0 +1,3 @@
+2520 is the smallest number that can be divided by each of the numbers from 1 to 10 without any remainder.
+
+What is the smallest positive number that is evenly divisible by all of the numbers from 1 to 20?
diff --git a/www/statics/euler/euler_005_explanation.md b/www/statics/euler/euler_005_explanation.md
new file mode 100644
index 0000000..ca57b32
--- /dev/null
+++ b/www/statics/euler/euler_005_explanation.md
@@ -0,0 +1,11 @@
+We start with a value of `1`.
+Then we multiply one after another the numbers from `1` to `20` to our value (We call these `multiplicand` in the loop).
+
+After each multiplications we search go through the numbers from `2` to `value` and search for a number `divisor` where
+
+ - `value % divisor == 0`
+ - `(value / divisor) % {0, multiplicand} == 0`
+
+Then (after we found such a number) we can reduce the value with it (`value /= divisor`).
+
+The reduction steps guarantees us that we find the **smallest** number and it prevents our *Int64* numbers from overflowing
\ No newline at end of file
diff --git a/www/statics/euler/euler_006.php b/www/statics/euler/euler_006.php
new file mode 100644
index 0000000..164a7cd
--- /dev/null
+++ b/www/statics/euler/euler_006.php
@@ -0,0 +1,19 @@
+ 6,
+ 'title' => 'Sum square difference',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_006_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_006_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_006_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=006',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-006.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 18897151,
+ 'time' => 7347,
+ 'width' => 72,
+ 'height' => 16,
+ 'value' => 25164150,
+];
diff --git a/www/statics/euler/euler_006_code.txt b/www/statics/euler/euler_006_code.txt
new file mode 100644
index 0000000..12bb68f
--- /dev/null
+++ b/www/statics/euler/euler_006_code.txt
@@ -0,0 +1,16 @@
+"d"10p000p>10g:00g+00p1-:#v_$010p>"c"10g::1+:*\:5:+%\5:+/6+p`#v_ v
+>$.@ ^ p01< ^ p01+1g01 < 0
+ > v
+|!:\<|p01-1:g01<$$_v#!:g+6/+:5\%+:5:g01 :< p01"c"+<_v#!p01:-1g01` > #v_v
+> v v-g+6/+:5\%+:5:g01< >00g ^
+##########> ^
+########## >010g:5:+%\5:+/6+pv
+##########
+########## ^ < <
+##########
+##########
+##########
+##########
+##########
+##########
\ No newline at end of file
diff --git a/www/statics/euler/euler_006_description.md b/www/statics/euler/euler_006_description.md
new file mode 100644
index 0000000..44d58f3
--- /dev/null
+++ b/www/statics/euler/euler_006_description.md
@@ -0,0 +1,9 @@
+The sum of the squares of the first ten natural numbers is,
+`1^2 + 2^2 + ... + 10^2 = 385`
+
+The square of the sum of the first ten natural numbers is,
+`(1 + 2 + ... + 10)^2 = 552 = 3025`
+
+Hence the difference between the sum of the squares of the first ten natural numbers and the square of the sum is `3025 - 385 = 2640`.
+
+Find the difference between the sum of the squares of the first one hundred natural numbers and the square of the sum.
\ No newline at end of file
diff --git a/www/statics/euler/euler_006_explanation.md b/www/statics/euler/euler_006_explanation.md
new file mode 100644
index 0000000..088604c
--- /dev/null
+++ b/www/statics/euler/euler_006_explanation.md
@@ -0,0 +1,7 @@
+My solution here is *far* more complex than necessary, mostly because I thought the temporary numbers would get too big for int32 to handle (especially sum(1,100)^2).
+Later I found out I could just calculate the sum of the squares and the square of the sum and subtract them ...
+
+But I like my solution so I'll leave it here.
+While I calculate the the second value (using the distributive property), I subtract in every step as much parts of the first value (the single elements of the addition) as I can (without going negative).
+
+That way my temporary values never greatly exceed the final result.
\ No newline at end of file
diff --git a/www/statics/euler/euler_007.php b/www/statics/euler/euler_007.php
new file mode 100644
index 0000000..e156475
--- /dev/null
+++ b/www/statics/euler/euler_007.php
@@ -0,0 +1,19 @@
+ 7,
+ 'title' => '10001st prime',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_007_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_007_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_007_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=007',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-007.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 21915385,
+ 'time' => 7628,
+ 'width' => 1000,
+ 'height' => 156,
+ 'value' => 104743,
+];
diff --git a/www/statics/euler/euler_007_code.txt b/www/statics/euler/euler_007_code.txt
new file mode 100644
index 0000000..30f2de4
--- /dev/null
+++ b/www/statics/euler/euler_007_code.txt
@@ -0,0 +1,11 @@
+v
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+ v <
+>"d"55+*:10p3"2"*:20p*00p230p" ":01p11p10g5:+*1+50pv > 030p 040p>30g1+:30p:10g%\10g/1+g"X"- |
+v < _^#`g03g00 <|p+1/g01\%g01:g03"0"-p04:+1g04g05<
+> "X" 30g:10g%\10g/1+p30g >30g+ : 00g\` #v_$>30g1+:30p:10g%\10g/1+g" "- |>30g.@
+ ^p+1/g01\%g01:\" ":< ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_007_description.md b/www/statics/euler/euler_007_description.md
new file mode 100644
index 0000000..a808c0f
--- /dev/null
+++ b/www/statics/euler/euler_007_description.md
@@ -0,0 +1,3 @@
+By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13.
+
+What is the 10 001st prime number?
\ No newline at end of file
diff --git a/www/statics/euler/euler_007_explanation.md b/www/statics/euler/euler_007_explanation.md
new file mode 100644
index 0000000..69502cc
--- /dev/null
+++ b/www/statics/euler/euler_007_explanation.md
@@ -0,0 +1 @@
+Finally a opportunity to use my favorite algorithm: [The sieve of Eratosthenes.](http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes)
\ No newline at end of file
diff --git a/www/statics/euler/euler_008.php b/www/statics/euler/euler_008.php
new file mode 100644
index 0000000..a65a5f3
--- /dev/null
+++ b/www/statics/euler/euler_008.php
@@ -0,0 +1,19 @@
+ 8,
+ 'title' => 'Largest product in a series',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_008_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_008_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_008_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=008',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-008.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 614295,
+ 'time' => 234,
+ 'width' => 116,
+ 'height' => 29,
+ 'value' => 23514624000,
+];
diff --git a/www/statics/euler/euler_008_code.txt b/www/statics/euler/euler_008_code.txt
new file mode 100644
index 0000000..05c712a
--- /dev/null
+++ b/www/statics/euler/euler_008_code.txt
@@ -0,0 +1,29 @@
+"v"00p54*:10p552**:20p*30p85+40p050p060p070p080p v
+>150g60p>60g:20g%\20g/9+g"0"-*60g1+:60p50g-40g-#v_:80g`#v_$>50g1+:50p30g-#v_ 970p >70g0g.70g8-40g-#v_"=",80g.@
+ ^ < $ ^ <
+ >80p060p>60g50g+:2 0g%\20g /9+g"0"-60g9+0p6 0g1+:60p40g-#v_^
+^ < < ^p07+1g07 <
+ ^ <
+
+
+
+73167176531330624919225119674426574742355349194934
+96983520312774506326239578318016984801869478851843
+85861560789112949495459501737958331952853208805511
+12540698747158523863050715693290963295227443043557
+66896648950445244523161731856403098711121722383113
+62229893423380308135336276614282806444486645238749
+30358907296290491560440772390713810515859307960866
+70172427121883998797908792274921901699720888093776
+65727333001053367881220235421809751254540594752243
+52584907711670556013604839586446706324415722155397
+53697817977846174064955149290862569321978468622482
+83972241375657056057490261407972968652414535100474
+82166370484403199890008895243450658541227588666881
+16427171479924442928230863465674813919123162824586
+17866458359124566529476545682848912883142607690042
+24219022671055626321111109370544217506941658960408
+07198403850962455444362981230987879927244284909188
+84580156166097919133875499200524063689912560717606
+05886116467109405077541002256983155200055935729725
+71636269561882670428252483600823257530420752963450
\ No newline at end of file
diff --git a/www/statics/euler/euler_008_description.md b/www/statics/euler/euler_008_description.md
new file mode 100644
index 0000000..f4b345b
--- /dev/null
+++ b/www/statics/euler/euler_008_description.md
@@ -0,0 +1,7 @@
+The four adjacent digits in the 1000-digit number that have the greatest product are 9 × 9 × 8 × 9 = 5832.
+
+```
+...
+```
+
+Find the thirteen adjacent digits in the 1000-digit number that have the greatest product. What is the value of this product?
diff --git a/www/statics/euler/euler_008_explanation.md b/www/statics/euler/euler_008_explanation.md
new file mode 100644
index 0000000..80e0ff6
--- /dev/null
+++ b/www/statics/euler/euler_008_explanation.md
@@ -0,0 +1 @@
+These kinds of problems are fun in Befunge because you can just copy the input into your program and it becomes a part of your source code.
\ No newline at end of file
diff --git a/www/statics/euler/euler_009.php b/www/statics/euler/euler_009.php
new file mode 100644
index 0000000..e332cd5
--- /dev/null
+++ b/www/statics/euler/euler_009.php
@@ -0,0 +1,19 @@
+ 9,
+ 'title' => 'Special Pythagorean triplet',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_009_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_009_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_009_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=009',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-009.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 1397212134,
+ 'time' => 394277,
+ 'width' => 79,
+ 'height' => 7,
+ 'value' => 31875000,
+];
diff --git a/www/statics/euler/euler_009_code.txt b/www/statics/euler/euler_009_code.txt
new file mode 100644
index 0000000..d83baee
--- /dev/null
+++ b/www/statics/euler/euler_009_code.txt
@@ -0,0 +1,7 @@
+"d"5:+*00p210p> 120p>v >20g1+:20p10g-#v_10g1+:10p00g-#v_ @
+ ^ <
+ ^ <
+v <
+>20g:*10g:*+:30p0>::*30g-#v_:30p20g10g++ 00g-#v_20g:." ",10g:." ",30g:."=",**.@
+ |-g00 :+1<
+ >$$ ^ $<
\ No newline at end of file
diff --git a/www/statics/euler/euler_009_description.md b/www/statics/euler/euler_009_description.md
new file mode 100644
index 0000000..2d613ad
--- /dev/null
+++ b/www/statics/euler/euler_009_description.md
@@ -0,0 +1,7 @@
+A Pythagorean triplet is a set of three natural numbers, a < b < c, for which,
+`a^2 + b^2 = c^2`
+
+For example, 3^2 + 4^2 = 9 + 16 = 25 = 5^2.
+
+There exists exactly one Pythagorean triplet for which a + b + c = 1000.
+Find the product abc.
\ No newline at end of file
diff --git a/www/statics/euler/euler_009_explanation.md b/www/statics/euler/euler_009_explanation.md
new file mode 100644
index 0000000..92aa2b2
--- /dev/null
+++ b/www/statics/euler/euler_009_explanation.md
@@ -0,0 +1 @@
+The brute-force approach is here taking quite a long time - but I think it's good enough - perhaps I will make an optimized version later
\ No newline at end of file
diff --git a/www/statics/euler/euler_010.php b/www/statics/euler/euler_010.php
new file mode 100644
index 0000000..4b1226e
--- /dev/null
+++ b/www/statics/euler/euler_010.php
@@ -0,0 +1,19 @@
+ 10,
+ 'title' => 'Summation of primes',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_010_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_010_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_010_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=010',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-010.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 416776174,
+ 'time' => 67127,
+ 'width' => 2000,
+ 'height' => 1007,
+ 'value' => 142913828922,
+];
diff --git a/www/statics/euler/euler_010_code.txt b/www/statics/euler/euler_010_code.txt
new file mode 100644
index 0000000..75d2023
--- /dev/null
+++ b/www/statics/euler/euler_010_code.txt
@@ -0,0 +1,12 @@
+v
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+>"d"55+*:2**1- >:"#"\:"d"55+2**%\"d"55+2**/1+p:#v_ "d"55+*:2*:10p v
+^ ^ -1< v p05+1*+:5g01p11p10:" "p032p00*p02: 030p 040p>30g1+:30p:10g% \10g/1+g"X"-|
+v < _^#`g03g00 <| - g03g00 < p04+g04 g03<
+> "X" 30g:10g%\10g/1+p30g >30g+ : 00g\` #v_$>30g1+:30p:10g%\10g/1+g" "- |>40g.@
+ ^p+1/g01\%g01:\" ":< ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_010_description.md b/www/statics/euler/euler_010_description.md
new file mode 100644
index 0000000..90ba691
--- /dev/null
+++ b/www/statics/euler/euler_010_description.md
@@ -0,0 +1,3 @@
+The sum of the primes below 10 is 2 + 3 + 5 + 7 = 17.
+
+Find the sum of all the primes below two million.
diff --git a/www/statics/euler/euler_010_explanation.md b/www/statics/euler/euler_010_explanation.md
new file mode 100644
index 0000000..7d29e12
--- /dev/null
+++ b/www/statics/euler/euler_010_explanation.md
@@ -0,0 +1 @@
+And again a sieve of Eratosthenes (see Problem 7), but this time a lot bigger.
\ No newline at end of file
diff --git a/www/statics/euler/euler_011.php b/www/statics/euler/euler_011.php
new file mode 100644
index 0000000..afee53b
--- /dev/null
+++ b/www/statics/euler/euler_011.php
@@ -0,0 +1,19 @@
+ 11,
+ 'title' => 'Largest product in a grid',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_011_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_011_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_011_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=011',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-011.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 323945,
+ 'time' => 78,
+ 'width' => 151,
+ 'height' => 31,
+ 'value' => 70600674,
+];
diff --git a/www/statics/euler/euler_011_code.txt b/www/statics/euler/euler_011_code.txt
new file mode 100644
index 0000000..eb55da7
--- /dev/null
+++ b/www/statics/euler/euler_011_code.txt
@@ -0,0 +1,31 @@
+v v <
+>"4"2/:*1-00p > 000g: "4"2/ %"?"+\ "4"2/ /1+ p 00g:1-00p #^_v++++++++++++++++++++++++++
+ ++++++++++++++++++++++++++
+ ++++++++++++++++++++++++++
+ 08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08 | +++####################+++
+ 49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00 | +++####################+++
+ 81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65 | +++####################+++
+ 52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91 | +++####################+++
+ 22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80 | +++####################+++
+ 24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50 | +++####################+++
+ 32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70 | +++####################+++
+ 67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21 | +++####################+++
+ 24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72 | +++####################+++
+ 21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95 | +++####################+++
+ 78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92 | +++####################+++
+ 16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57 | +++####################+++
+ 86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58 | +++####################+++
+ 19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40 | +++####################+++
+ 04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66 | +++####################+++
+ 88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69 | +++####################+++
+ 04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36 | +++####################+++
+ 20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16 | +++####################+++
+ 20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54 | +++####################+++
+ 01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48 | +++####################+++
+vp00-1*:*45 p1++1550p0++1551p1+55-10p0+551p19-10p090 p010<++++++++++++++++++++++++++ >10pv
+>00g:54*%3*1+\54*/4+g"0"-52**00g:54*%3*2+\54*/4+g"0"-+00g:54*%v++++++++++++++++++++++++++ >$> v
+| p00-1:g00p+4/*45\+"B"<++++++++++++++++++++++++++ ^_^#`g01:< v <
+>54*:*1-00p>220p>20g9+:0g30p1g40p00g:54*%50p54*/60p50g"B"+60g4+g50g30g+50p60g40g+60p>50g"B"+60g4+g50g30g+50p60g40g+60pv >20g:1-20p#v_00g:1-00p#^_10g. @
+ ^ _^# 50g"B"+60g4+g50g30g+50p60g40g+60p***^
+ ^ <<
\ No newline at end of file
diff --git a/www/statics/euler/euler_011_description.md b/www/statics/euler/euler_011_description.md
new file mode 100644
index 0000000..c9adc54
--- /dev/null
+++ b/www/statics/euler/euler_011_description.md
@@ -0,0 +1,9 @@
+In the 20×20 grid below, four numbers along a diagonal line have been marked in red.
+
+```
+...
+```
+
+The product of these numbers is 26 × 63 × 78 × 14 = 1788696.
+
+What is the greatest product of four adjacent numbers in the same direction (up, down, left, right, or diagonally) in the 20×20 grid?
\ No newline at end of file
diff --git a/www/statics/euler/euler_011_explanation.md b/www/statics/euler/euler_011_explanation.md
new file mode 100644
index 0000000..9a8b9c4
--- /dev/null
+++ b/www/statics/euler/euler_011_explanation.md
@@ -0,0 +1 @@
+The idea here was to first move the numbers into a *real* 20x20 grid where every field represents a single number, the rest was not that hard.
\ No newline at end of file
diff --git a/www/statics/euler/euler_012.php b/www/statics/euler/euler_012.php
new file mode 100644
index 0000000..cfd89c5
--- /dev/null
+++ b/www/statics/euler/euler_012.php
@@ -0,0 +1,19 @@
+ 12,
+ 'title' => 'Highly divisible triangular number',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_012_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_012_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_012_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=012',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-012.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 38855123,
+ 'time' => 7566,
+ 'width' => 1000,
+ 'height' => 170,
+ 'value' => 76576500,
+];
diff --git a/www/statics/euler/euler_012_code.txt b/www/statics/euler/euler_012_code.txt
new file mode 100644
index 0000000..223489b
--- /dev/null
+++ b/www/statics/euler/euler_012_code.txt
@@ -0,0 +1,22 @@
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+ v p03+1g03 p04+1g04 p +3/g01\%g01:g04 g03 <
+>"d"55+*:10p3"2"*:20p*00p230p" ":03p13p v >130p040p > 30g:10g%\10g/3+g" "- 00g30g` !#v_ |
+v < _^#`g03g00 <^ p03+1g03 <
+> "X" 30g:10g%\10g/3+p30g >30g+ : 00g\` #v_$>30g1+:30p:10g%\10g/3+g" "- |
+ ^p+3/g01\%g01:\" ":< ^ <
+ v +1$<
+ >:1+2/>:01p31p111p0>::10g%\10g/3+g::*01g`#v_121p>:31g\% !#v_11g21g*11p31g1-|
+ v < ^p13/\g13:p12+1g12<
+ v < vp21<*2g11$$<^g11$$ <
+>2 212p222p >:2%| >12g22g*"d"5*` #v_1+ 1v
+ | < 0+1$<
+ >:1+ >:01p31p111p0>::10g%\10g/3+g::*01g`#v_121p>:31g\% !#v_11g21g*11p31g1-|
+ # v < v ^p13/\g13:p12+1g12<
+ ^p22<*2g11$$<^g11$$ <
+ >$$:1+*2/.@
+^ $p05-1g04<
\ No newline at end of file
diff --git a/www/statics/euler/euler_012_description.md b/www/statics/euler/euler_012_description.md
new file mode 100644
index 0000000..484cf46
--- /dev/null
+++ b/www/statics/euler/euler_012_description.md
@@ -0,0 +1,17 @@
+The sequence of triangle numbers is generated by adding the natural numbers. So the 7th triangle number would be 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. The first ten terms would be:
+
+1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...
+
+Let us list the factors of the first seven triangle numbers:
+
+ 1: 1
+ 3: 1,3
+ 6: 1,2,3,6
+10: 1,2,5,10
+15: 1,3,5,15
+21: 1,3,7,21
+28: 1,2,4,7,14,28
+
+We can see that 28 is the first triangle number to have over five divisors.
+
+What is the value of the first triangle number to have over five hundred divisors?
\ No newline at end of file
diff --git a/www/statics/euler/euler_012_explanation.md b/www/statics/euler/euler_012_explanation.md
new file mode 100644
index 0000000..c455f6a
--- /dev/null
+++ b/www/statics/euler/euler_012_explanation.md
@@ -0,0 +1 @@
+Here I was desperately in need of an efficient algorithm. So I copied [this](http://www.mathblog.dk/triangle-number-with-more-than-500-divisors/) one from mathblog.dk and translated it into befunge. And I have to say it's amazingly fast.
\ No newline at end of file
diff --git a/www/statics/euler/euler_013.php b/www/statics/euler/euler_013.php
new file mode 100644
index 0000000..edeab9d
--- /dev/null
+++ b/www/statics/euler/euler_013.php
@@ -0,0 +1,19 @@
+ 13,
+ 'title' => 'Large sum',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_013_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_013_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_013_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=013',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-013.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 244792,
+ 'time' => 78,
+ 'width' => 59,
+ 'height' => 113,
+ 'value' => 5537376230,
+];
diff --git a/www/statics/euler/euler_013_code.txt b/www/statics/euler/euler_013_code.txt
new file mode 100644
index 0000000..7bec3fe
--- /dev/null
+++ b/www/statics/euler/euler_013_code.txt
@@ -0,0 +1,16 @@
+v // Project Euler - Problem 13
+ 37107287533902102798797998220837590246510135740250
+ ...
+# 53503534226472524250874054075591789781264330331690
+=
+
+ v_v# < <1<
+>510p"d"20p>"0"10g20gp10g1-:10p#^_510p20g1-:20p#^_^
+v $<
+>"7"10pv>10g20gg" "-!#v_ >10g20gg"0"-00g+00p v
+v30p021< >10g1-10p55+/00p v |-" "gg02g01p02+1g02<
+>0p0::p ^^p021pg02g01+"0"%+55:<>0v
+ ^ "# $< ^g0<
+v p02"e"p010$<
+>10g1+:10p20gg"0"-!#v_55+00p>00g:1-00p!#@_54+00g-10g+20gg,v
+^ < ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_013_description.md b/www/statics/euler/euler_013_description.md
new file mode 100644
index 0000000..e4dd09d
--- /dev/null
+++ b/www/statics/euler/euler_013_description.md
@@ -0,0 +1,5 @@
+Work out the first ten digits of the sum of the following one-hundred 50-digit numbers.
+
+```
+...
+```
\ No newline at end of file
diff --git a/www/statics/euler/euler_013_explanation.md b/www/statics/euler/euler_013_explanation.md
new file mode 100644
index 0000000..8e4bb38
--- /dev/null
+++ b/www/statics/euler/euler_013_explanation.md
@@ -0,0 +1 @@
+Here I do simply do a column addition. After the sum is calculated, we take the first 10 digits and print them
\ No newline at end of file
diff --git a/www/statics/euler/euler_014.php b/www/statics/euler/euler_014.php
new file mode 100644
index 0000000..738f0bc
--- /dev/null
+++ b/www/statics/euler/euler_014.php
@@ -0,0 +1,19 @@
+ 14,
+ 'title' => 'Longest Collatz sequence',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_014_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_014_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_014_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=014',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-014.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 3877209672,
+ 'time' => 717713,
+ 'width' => 51,
+ 'height' => 5,
+ 'value' => 837799,
+];
diff --git a/www/statics/euler/euler_014_code.txt b/www/statics/euler/euler_014_code.txt
new file mode 100644
index 0000000..eccef8c
--- /dev/null
+++ b/www/statics/euler/euler_014_code.txt
@@ -0,0 +1,5 @@
+v >3*1+v
+>0::p3>1+:1\>:2%| >\1+\:1- #v_$:00g\`#v_00p:10pv
+v:0.g0 1< ^ $># 2/^#1 < $
+g ^_^#!` **"}}@": < <
+>": ",,.@
\ No newline at end of file
diff --git a/www/statics/euler/euler_014_description.md b/www/statics/euler/euler_014_description.md
new file mode 100644
index 0000000..c055861
--- /dev/null
+++ b/www/statics/euler/euler_014_description.md
@@ -0,0 +1,13 @@
+The following iterative sequence is defined for the set of positive integers:
+
+n -> n/2 (n is even)
+n -> 3n + 1 (n is odd)
+
+Using the rule above and starting with 13, we generate the following sequence:
+13 -> 40 -> 20 -> 10 -> 5 -> 16 -> 8 -> 4 -> 2 -> 1
+
+It can be seen that this sequence (starting at 13 and finishing at 1) contains 10 terms. Although it has not been proved yet (Collatz Problem), it is thought that all starting numbers finish at 1.
+
+Which starting number, under one million, produces the longest chain?
+
+NOTE: Once the chain starts the terms are allowed to go above one million.
\ No newline at end of file
diff --git a/www/statics/euler/euler_014_explanation.md b/www/statics/euler/euler_014_explanation.md
new file mode 100644
index 0000000..cd1ab79
--- /dev/null
+++ b/www/statics/euler/euler_014_explanation.md
@@ -0,0 +1 @@
+Again a simple problem, we get the length of every sequence (= until they reach `1`) and print the highest.
\ No newline at end of file
diff --git a/www/statics/euler/euler_015.php b/www/statics/euler/euler_015.php
new file mode 100644
index 0000000..691f14f
--- /dev/null
+++ b/www/statics/euler/euler_015.php
@@ -0,0 +1,19 @@
+ 15,
+ 'title' => 'Lattice paths',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_015_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_015_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_015_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=015',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-015.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 61202,
+ 'time' => 47,
+ 'width' => 78,
+ 'height' => 27,
+ 'value' => 137846528820,
+];
diff --git a/www/statics/euler/euler_015_code.txt b/www/statics/euler/euler_015_code.txt
new file mode 100644
index 0000000..7e6b436
--- /dev/null
+++ b/www/statics/euler/euler_015_code.txt
@@ -0,0 +1,27 @@
+v
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000
+ 000000000000000000000 > v
+ >v >00g1-10gg00g10g1-g+00g10gpv
+>100p110p> 00g492*+10g-*|>00g392*+`#^_>00g1-10g1-*| vp01+1g01p00-1g00<
+ ^p011p00+g01g00< >100g10gp ^
+ |! `+2*58+g00g01 <
+ @.g:*73<
\ No newline at end of file
diff --git a/www/statics/euler/euler_015_description.md b/www/statics/euler/euler_015_description.md
new file mode 100644
index 0000000..89b983e
--- /dev/null
+++ b/www/statics/euler/euler_015_description.md
@@ -0,0 +1,5 @@
+Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.
+
+
+
+How many such routes are there through a 20×20 grid?
\ No newline at end of file
diff --git a/www/statics/euler/euler_015_explanation.md b/www/statics/euler/euler_015_explanation.md
new file mode 100644
index 0000000..93debd3
--- /dev/null
+++ b/www/statics/euler/euler_015_explanation.md
@@ -0,0 +1,3 @@
+We create a 21x21 grid of the edges in our graph, then we set the value on each edge to the number of possible paths to (0|0).
+For the top-left edge this is `1`. For the edges in the first row/column it is also `1`. For every other edge it is the above edge + the left edge.
+And in the end we are only interested in the value of the bottom-right edge - this value is our result.
\ No newline at end of file
diff --git a/www/statics/euler/euler_016.php b/www/statics/euler/euler_016.php
new file mode 100644
index 0000000..f0698dc
--- /dev/null
+++ b/www/statics/euler/euler_016.php
@@ -0,0 +1,19 @@
+ 16,
+ 'title' => 'Power digit sum',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_016_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_016_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_016_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=016',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-016.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 27332672,
+ 'time' => 4228,
+ 'width' => 60,
+ 'height' => 14,
+ 'value' => 1366,
+];
diff --git a/www/statics/euler/euler_016_code.txt b/www/statics/euler/euler_016_code.txt
new file mode 100644
index 0000000..e9381fd
--- /dev/null
+++ b/www/statics/euler/euler_016_code.txt
@@ -0,0 +1,14 @@
+v00000000000000000000000000000000000000000000000000000000000
+v00000000000000000000000000000000000000000000000000000000000
+v00000000000000000000000000000000000000000000000000000000000
+v00000000000000000000000000000000000000000000000000000000000
+v00000000000000000000000000000000000000000000000000000000000
+v00000000000000000000000000000000000000000000000000000000001
+
+> "0":::::00p01p02p03p04p05p v // INIT
+v p64*8"}"p60*p62:6p61:"<" 06g1-66p 0> 66g16g%66g16g/g"0"-+ 66g|
+v $# < .
+>46g:!#^_ 1-46p 06g1-66p 076p > 66g!#^_ v @
+v61g66+"0"%+55:+g67*2-"0"g/g61 g66%g61g66<
+>g%66g16g/p55+/76p 66g1-66p ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_016_description.md b/www/statics/euler/euler_016_description.md
new file mode 100644
index 0000000..ce81435
--- /dev/null
+++ b/www/statics/euler/euler_016_description.md
@@ -0,0 +1,3 @@
+2^15 = 32768 and the sum of its digits is 3 + 2 + 7 + 6 + 8 = 26.
+
+What is the sum of the digits of the number 2^1000?
\ No newline at end of file
diff --git a/www/statics/euler/euler_016_explanation.md b/www/statics/euler/euler_016_explanation.md
new file mode 100644
index 0000000..771086c
--- /dev/null
+++ b/www/statics/euler/euler_016_explanation.md
@@ -0,0 +1 @@
+Here I implemented a long multiplication algorithm. Then I took the value `1` and doubled it 1000 times. The calculation of the digit sum was then easy.
\ No newline at end of file
diff --git a/www/statics/euler/euler_017.php b/www/statics/euler/euler_017.php
new file mode 100644
index 0000000..fe0a872
--- /dev/null
+++ b/www/statics/euler/euler_017.php
@@ -0,0 +1,19 @@
+ 17,
+ 'title' => 'Number letter counts',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_017_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_017_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_017_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=017',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-017.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 179076,
+ 'time' => 47,
+ 'width' => 48,
+ 'height' => 15,
+ 'value' => 21124,
+];
diff --git a/www/statics/euler/euler_017_code.txt b/www/statics/euler/euler_017_code.txt
new file mode 100644
index 0000000..8636343
--- /dev/null
+++ b/www/statics/euler/euler_017_code.txt
@@ -0,0 +1,15 @@
+v
+033544355436688779886
+0366555766
+$
+$ v-1 < v-1 <
+>54*>:::1g"0"-\1p#^_54*>:::2g"0"-\2p|
+v **25"d" 0 $$<
+v <
+ v $< >:55+/2g\55+% v
+: >:54*`| >"d"/1g70 v
+>0\>:!#v_:"d"\`| ^0g1< >:"d"%!| v <
+v < >:"}"8*-#^_$380v>:"d"/1g\ "d"%v
+ ^ < <\3\7<
+>+# \:# _+ \ 1- :|
+ @.+_ #! #:\ #+<
\ No newline at end of file
diff --git a/www/statics/euler/euler_017_description.md b/www/statics/euler/euler_017_description.md
new file mode 100644
index 0000000..b2d272a
--- /dev/null
+++ b/www/statics/euler/euler_017_description.md
@@ -0,0 +1,5 @@
+If the numbers 1 to 5 are written out in words: one, two, three, four, five, then there are 3 + 3 + 5 + 4 + 4 = 19 letters used in total.
+
+If all the numbers from 1 to 1000 (one thousand) inclusive were written out in words, how many letters would be used?
+
+*NOTE: Do not count spaces or hyphens. For example, 342 (three hundred and forty-two) contains 23 letters and 115 (one hundred and fifteen) contains 20 letters. The use of "and" when writing out numbers is in compliance with British usage.*
\ No newline at end of file
diff --git a/www/statics/euler/euler_017_explanation.md b/www/statics/euler/euler_017_explanation.md
new file mode 100644
index 0000000..3f82bac
--- /dev/null
+++ b/www/statics/euler/euler_017_explanation.md
@@ -0,0 +1,8 @@
+There are only `N` kinds of numbers:
+
+- `0` - `20`: Get the length from a precomputed list
+- `20` - `99`: Get the length of the first word from a precomputed list and the length of the second word (second digit) from the previous point
+- `100` - `999`: Get the length of the first word from a precomputed list and the length of the second and third word (second digit) from the previous point
+- `1000`: Get the hard coded value
+
+*Note*: Interestingly this program operates completely on the stack - only the initializing method sets a few "constant fields" to per-definied values
\ No newline at end of file
diff --git a/www/statics/euler/euler_018.php b/www/statics/euler/euler_018.php
new file mode 100644
index 0000000..6e55250
--- /dev/null
+++ b/www/statics/euler/euler_018.php
@@ -0,0 +1,19 @@
+ 18,
+ 'title' => 'Maximum path sum I',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_018_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_018_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_018_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=018',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-018.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 15048,
+ 'time' => 16,
+ 'width' => 120,
+ 'height' => 16,
+ 'value' => 1074,
+];
diff --git a/www/statics/euler/euler_018_code.txt b/www/statics/euler/euler_018_code.txt
new file mode 100644
index 0000000..2aa0b9c
--- /dev/null
+++ b/www/statics/euler/euler_018_code.txt
@@ -0,0 +1,16 @@
+$$>53* 00p00g1-20p010p>10g3*:20g1+g"0"-55+*\1+20g1+g"0"-+10g20g1+p10g1+:10p20g-1-#v_20g:1-20p010p#v_v
+75 ^ < < v
+95 64 v <
+17 47 82 > $v
+18 35 87 10 >00g2-:10p20p>10g20g1+g10g20g2+g:10g1+20g2+g -:0`>#^_->+10g20g1+p10g:1-10p#v_20g:1-:20p10p#v_01g.@
+20 04 82 47 65 ^ < <
+19 01 23 75 03 34
+88 02 77 73 07 63 67
+99 65 04 28 06 16 70 92
+41 41 26 56 83 40 80 70 33
+41 48 72 33 47 32 37 16 94 29
+53 71 44 65 25 43 91 52 97 51 14
+70 11 33 28 77 73 17 78 39 68 17 57
+91 71 52 38 17 14 91 43 58 50 27 29 48
+63 66 04 68 89 53 67 30 73 16 69 87 40 31
+04 62 98 27 23 09 70 98 73 93 38 53 60 04 23
\ No newline at end of file
diff --git a/www/statics/euler/euler_018_description.md b/www/statics/euler/euler_018_description.md
new file mode 100644
index 0000000..4bb3ea7
--- /dev/null
+++ b/www/statics/euler/euler_018_description.md
@@ -0,0 +1,18 @@
+By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
+
+~~~
+3
+7 4
+2 4 6
+8 5 9 3
+~~~
+
+That is, 3 + 7 + 4 + 9 = 23.
+
+Find the maximum total from top to bottom of the triangle below:
+
+~~~
+...
+~~~
+
+*NOTE: As there are only 16384 routes, it is possible to solve this problem by trying every route. However, Problem 67, is the same challenge with a triangle containing one-hundred rows; it cannot be solved by brute force, and requires a clever method! ;o)*
\ No newline at end of file
diff --git a/www/statics/euler/euler_018_explanation.md b/www/statics/euler/euler_018_explanation.md
new file mode 100644
index 0000000..0a20d51
--- /dev/null
+++ b/www/statics/euler/euler_018_explanation.md
@@ -0,0 +1,5 @@
+Step 1: Convert the numbers so that 1 field = 1 number
+
+Step 2: Set every field to `value` + max(`value-left`, `value-right`)
+
+Step 3: The solution is the value of the top-most field
\ No newline at end of file
diff --git a/www/statics/euler/euler_019.php b/www/statics/euler/euler_019.php
new file mode 100644
index 0000000..a8ccc4c
--- /dev/null
+++ b/www/statics/euler/euler_019.php
@@ -0,0 +1,19 @@
+ 19,
+ 'title' => 'Counting Sundays',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_019_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_019_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_019_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=019',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-019.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 3197878,
+ 'time' => 546,
+ 'width' => 72,
+ 'height' => 12,
+ 'value' => 171,
+];
diff --git a/www/statics/euler/euler_019_code.txt b/www/statics/euler/euler_019_code.txt
new file mode 100644
index 0000000..4fbc8c9
--- /dev/null
+++ b/www/statics/euler/euler_019_code.txt
@@ -0,0 +1,12 @@
+v303232332323
+v313232332323
+6
+>2*>::0g"0"-47*+\0p::v
+ |:-1p1\+*74-"0"g1 <
+v $<
+>202p112p122p"2&"*1+32p092pv
+v20+1g20p29+g29!+-1g21%7g20<># 0# v# < > >v
+>p12g1+12p32g4% | >1 >>22g\g12g1--|
+ >32g"d"%| 0^ < # >112p22g:1+22p66+-|
+ v%*4"d"g23<>#^_1^ |-+1*"(2"g23 ^>1^ >92g.@ ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_019_description.md b/www/statics/euler/euler_019_description.md
new file mode 100644
index 0000000..2bad72c
--- /dev/null
+++ b/www/statics/euler/euler_019_description.md
@@ -0,0 +1,12 @@
+You are given the following information, but you may prefer to do some research for yourself.
+
+ - 1 Jan 1900 was a Monday.
+ - Thirty days has September,
+ - April, June and November.
+ - All the rest have thirty-one,
+ - Saving February alone,
+ - Which has twenty-eight, rain or shine.
+ - And on leap years, twenty-nine.
+ - A leap year occurs on any year evenly divisible by 4, but not on a century unless it is divisible by 400.
+
+How many Sundays fell on the first of the month during the twentieth century (1 Jan 1901 to 31 Dec 2000)?
\ No newline at end of file
diff --git a/www/statics/euler/euler_019_explanation.md b/www/statics/euler/euler_019_explanation.md
new file mode 100644
index 0000000..5c04f6e
--- /dev/null
+++ b/www/statics/euler/euler_019_explanation.md
@@ -0,0 +1,3 @@
+In the first two rows we remember the day-count of each month.
+First row is normal years, second row leap years.
+Then we just enumerate through all days and test if its a Sunday and the first of month.
\ No newline at end of file
diff --git a/www/statics/euler/euler_020.php b/www/statics/euler/euler_020.php
new file mode 100644
index 0000000..53521c5
--- /dev/null
+++ b/www/statics/euler/euler_020.php
@@ -0,0 +1,19 @@
+ 20,
+ 'title' => 'Factorial digit sum',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_020_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_020_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_020_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=020',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-020.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 1546679,
+ 'time' => 265,
+ 'width' => 101,
+ 'height' => 6,
+ 'value' => 648,
+];
diff --git a/www/statics/euler/euler_020_code.txt b/www/statics/euler/euler_020_code.txt
new file mode 100644
index 0000000..a333625
--- /dev/null
+++ b/www/statics/euler/euler_020_code.txt
@@ -0,0 +1,6 @@
+v00 ... 00
+v00 ... 01
+>"d">1-:!#v_:03p013p"~I"+23p>23g"d"%1+23g"d"/g"0"-03g*13g+:55+%68 v
+ ^ $# _^#!p32:-1g32p31/+55p/"d"g32+1%"d"g32+*<
+ >"~I"+33p0>33g"d"%1+33g"d"/g"0"-+ 33g:1-33p v
+ @._^#! <
\ No newline at end of file
diff --git a/www/statics/euler/euler_020_description.md b/www/statics/euler/euler_020_description.md
new file mode 100644
index 0000000..b8dd5fb
--- /dev/null
+++ b/www/statics/euler/euler_020_description.md
@@ -0,0 +1,6 @@
+n! means n × (n - 1) × ... × 3 × 2 × 1
+
+For example, 10! = 10 × 9 × ... × 3 × 2 × 1 = 3628800,
+and the sum of the digits in the number 10! is 3 + 6 + 2 + 8 + 8 + 0 + 0 = 27.
+
+Find the sum of the digits in the number 100!
\ No newline at end of file
diff --git a/www/statics/euler/euler_020_explanation.md b/www/statics/euler/euler_020_explanation.md
new file mode 100644
index 0000000..3e759e4
--- /dev/null
+++ b/www/statics/euler/euler_020_explanation.md
@@ -0,0 +1,2 @@
+The approach is similar to problem 16 - the main task was implementing a long multiplication algorithm in Befunge.
+Then, after 100! is calculated we only need to sum the individual digits.
\ No newline at end of file
diff --git a/www/statics/euler/euler_021.php b/www/statics/euler/euler_021.php
new file mode 100644
index 0000000..c8ec230
--- /dev/null
+++ b/www/statics/euler/euler_021.php
@@ -0,0 +1,19 @@
+ 21,
+ 'title' => 'Amicable numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_021_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_021_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_021_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=021',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-021.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 601124986,
+ 'time' => 102399,
+ 'width' => 400,
+ 'height' => 33,
+ 'value' => 31626,
+];
diff --git a/www/statics/euler/euler_021_code.txt b/www/statics/euler/euler_021_code.txt
new file mode 100644
index 0000000..92ca244
--- /dev/null
+++ b/www/statics/euler/euler_021_code.txt
@@ -0,0 +1,13 @@
+v
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+ v ># v# <
+>"d"4*:10p55**00p00g>1-::20p0\2/>:20g\%#^_:30p+30g>1-:#^_$v
+ |: p+1/g01g02%g01g02<
+v$$ p100<
+>00g1-20p090p>20g10g%20g10g/1+g40p40g10g%40g10g/1+g50p 20g50g-#v_20g40g`!#v_20g." - ",,,40g.55+,v
+ |p02-1:g02 < < p09++g04g02g09<
+ @.g09<
\ No newline at end of file
diff --git a/www/statics/euler/euler_021_description.md b/www/statics/euler/euler_021_description.md
new file mode 100644
index 0000000..4873868
--- /dev/null
+++ b/www/statics/euler/euler_021_description.md
@@ -0,0 +1,6 @@
+Let d(n) be defined as the sum of proper divisors of n (numbers less than n which divide evenly into n).
+If d(a) = b and d(b) = a, where a ? b, then a and b are an amicable pair and each of a and b are called amicable numbers.
+
+For example, the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 and 110; therefore d(220) = 284. The proper divisors of 284 are 1, 2, 4, 71 and 142; so d(284) = 220.
+
+Evaluate the sum of all the amicable numbers under 10000.
\ No newline at end of file
diff --git a/www/statics/euler/euler_021_explanation.md b/www/statics/euler/euler_021_explanation.md
new file mode 100644
index 0000000..5d8776f
--- /dev/null
+++ b/www/statics/euler/euler_021_explanation.md
@@ -0,0 +1,2 @@
+Most of the time is here spent in the NumberOfDivisors function. So we first cache every possible result of this function (from 0 to 10000).
+The rest is simple searching for numbers where a == D(D(a)) and a != D(a).
\ No newline at end of file
diff --git a/www/statics/euler/euler_022.php b/www/statics/euler/euler_022.php
new file mode 100644
index 0000000..189b839
--- /dev/null
+++ b/www/statics/euler/euler_022.php
@@ -0,0 +1,19 @@
+ 22,
+ 'title' => 'Names scores',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_022_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_022_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_022_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=022',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-022.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 4703607994,
+ 'time' => 961793,
+ 'width' => 109,
+ 'height' => 5164,
+ 'value' => 871198282,
+];
diff --git a/www/statics/euler/euler_022_code.txt b/www/statics/euler/euler_022_code.txt
new file mode 100644
index 0000000..a674c33
--- /dev/null
+++ b/www/statics/euler/euler_022_code.txt
@@ -0,0 +1,13 @@
+> v // Calc ordered index > v
+ MARY >"??IE"*++:20p00p>010p0 >:00gg"@"-:0`#^_$0>10g74**+10pv
+ PATRICIA > ^ ^ _v# -+66:+1<
+ LINDA v _^#!p00:-1g00pg000g01$< >v // Bubblesort it
+ BARBARA >20g30p> 040p> 040g1+g 040g2+g`|>40g:1+>60p70p66+:80p>:60g1+g\70g1+g80g60g1+v
+ ELIZABETH |`\-1g03 p04:+1g04< $<|\p08:-1:g08p+1g07g08p <
+ JENNIFER |-2p03-1:g03< // Sum the values ^<
+ MARIA v 090p20g50p>1>:50gg:" " -|
+ MARGARET |p05:-1g05 $$$<
+ DOROTHY @.g09<
+ ...
+ ...
\ No newline at end of file
diff --git a/www/statics/euler/euler_022_description.md b/www/statics/euler/euler_022_description.md
new file mode 100644
index 0000000..f2e66d1
--- /dev/null
+++ b/www/statics/euler/euler_022_description.md
@@ -0,0 +1,5 @@
+Using names.txt (right click and 'Save Link/Target As...'), a 46K text file containing over five-thousand first names, begin by sorting it into alphabetical order. Then working out the alphabetical value for each name, multiply this value by its alphabetical position in the list to obtain a name score.
+
+For example, when the list is sorted into alphabetical order, COLIN, which is worth 3 + 15 + 12 + 9 + 14 = 53, is the 938th name in the list. So, COLIN would obtain a score of 938 × 53 = 49714.
+
+What is the total of all the name scores in the file?
\ No newline at end of file
diff --git a/www/statics/euler/euler_022_explanation.md b/www/statics/euler/euler_022_explanation.md
new file mode 100644
index 0000000..008db66
--- /dev/null
+++ b/www/statics/euler/euler_022_explanation.md
@@ -0,0 +1,2 @@
+The main thing here was sorting the list. I used [bubble sort](http://en.wikipedia.org/wiki/Bubble_sort), which is not the fastest algorithm but was pretty easy to implement in befunge.
+The rest is just calculating the single scores.
\ No newline at end of file
diff --git a/www/statics/euler/euler_023.php b/www/statics/euler/euler_023.php
new file mode 100644
index 0000000..06fc641
--- /dev/null
+++ b/www/statics/euler/euler_023.php
@@ -0,0 +1,19 @@
+ 23,
+ 'title' => 'Non-abundant sums',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_023_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_023_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_023_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=023',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-023.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 10667174483,
+ 'time' => 1967688,
+ 'width' => 400,
+ 'height' => 88,
+ 'value' => 4179871,
+];
diff --git a/www/statics/euler/euler_023_code.txt b/www/statics/euler/euler_023_code.txt
new file mode 100644
index 0000000..08a88c8
--- /dev/null
+++ b/www/statics/euler/euler_023_code.txt
@@ -0,0 +1,18 @@
+v
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+ v ># v# <
+>"d"4*:10p355***00p00g>1-::20p0\2/>:20g\%#^_:30p+30g>1-:#^_$v
+ |:p +1/g01g02%g01g02`g02<
+v $p100< vp+1/g01+g05g04%g01+g05g04+2%2g+1/g01+g05g04%g01+<
+$ >v >v >v >v v < g
+>00g40p>40g1-:40p|>40g10g%40g10g/1+g2%|>40g1+50p>50g1-:50p|>50g10g%50g10g/1+g2%|>40g50g+00g`| 0
+ ^ < ^ < $< >40g5^
+v < ^ <
+>080p00g20p>20g1-20p20g10g%20g10g/1+g2/#v_v
+ |g02 80g.@ ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_023_description.md b/www/statics/euler/euler_023_description.md
new file mode 100644
index 0000000..0459c12
--- /dev/null
+++ b/www/statics/euler/euler_023_description.md
@@ -0,0 +1,7 @@
+A perfect number is a number for which the sum of its proper divisors is exactly equal to the number. For example, the sum of the proper divisors of 28 would be 1 + 2 + 4 + 7 + 14 = 28, which means that 28 is a perfect number.
+
+A number n is called deficient if the sum of its proper divisors is less than n and it is called abundant if this sum exceeds n.
+
+As 12 is the smallest abundant number, 1 + 2 + 3 + 4 + 6 = 16, the smallest number that can be written as the sum of two abundant numbers is 24. By mathematical analysis, it can be shown that all integers greater than 28123 can be written as the sum of two abundant numbers. However, this upper limit cannot be reduced any further by analysis even though it is known that the greatest number that cannot be expressed as the sum of two abundant numbers is less than this limit.
+
+Find the sum of all the positive integers which cannot be written as the sum of two abundant numbers.
\ No newline at end of file
diff --git a/www/statics/euler/euler_023_explanation.md b/www/statics/euler/euler_023_explanation.md
new file mode 100644
index 0000000..efff7f9
--- /dev/null
+++ b/www/statics/euler/euler_023_explanation.md
@@ -0,0 +1,2 @@
+The algorithm here is pretty ineffecient. First I brute force all the abundent numbers and then calculate every possible product of these numbers.
+I used a little trick to store 2 boolean values per grid cell: The lowest bit represents if the value is abundent and the second-lowest if it can be written as two abundent numbers
\ No newline at end of file
diff --git a/www/statics/euler/euler_024.php b/www/statics/euler/euler_024.php
new file mode 100644
index 0000000..bb550f5
--- /dev/null
+++ b/www/statics/euler/euler_024.php
@@ -0,0 +1,19 @@
+ 24,
+ 'title' => 'Lexicographic permutations',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_024_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_024_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_024_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=024',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-024.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 3499,
+ 'time' => 31,
+ 'width' => 61,
+ 'height' => 8,
+ 'value' => 2783915460,
+];
diff --git a/www/statics/euler/euler_024_code.txt b/www/statics/euler/euler_024_code.txt
new file mode 100644
index 0000000..dac841a
--- /dev/null
+++ b/www/statics/euler/euler_024_code.txt
@@ -0,0 +1,8 @@
+v0123456789
+>"ddd"**1v
+vp129p11-<
+ >v>v v < v < > v >\1-\vv p14+1g14<
+>21g:1+|>|>21g0\>:1-:#^_$>*\:#^_$:| >31p 141p >31g41g*11g`!|
+ $ >$1^ |-"x" g0:\<\1 v> >1+\:| 1
+^p12-1g12p11-*-1g14g13g11.p0\"x"\-"0"g0:>#- #1 #$ #< ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_024_description.md b/www/statics/euler/euler_024_description.md
new file mode 100644
index 0000000..e7a2035
--- /dev/null
+++ b/www/statics/euler/euler_024_description.md
@@ -0,0 +1,5 @@
+A permutation is an ordered arrangement of objects. For example, 3124 is one possible permutation of the digits 1, 2, 3 and 4. If all of the permutations are listed numerically or alphabetically, we call it lexicographic order. The lexicographic permutations of 0, 1 and 2 are:
+
+012 021 102 120 201 210
+
+What is the millionth lexicographic permutation of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9?
\ No newline at end of file
diff --git a/www/statics/euler/euler_024_explanation.md b/www/statics/euler/euler_024_explanation.md
new file mode 100644
index 0000000..2f5e6ba
--- /dev/null
+++ b/www/statics/euler/euler_024_explanation.md
@@ -0,0 +1,11 @@
+This is a really nice problem - and I kinda like the solution.
+
+If we think about the ordered numbers we can see that the first few start with `0`, the next with `1` and so on ...
+We can also see that there are `8!` possible numbers that start with `0` (or any other digit).
+So if `1 * 8! <= (1000000 - 0)` the result starts with `0`. Otherwise if `2 * 8! <= (1000000 - 0)`, etc.
+Then after we got our first digit (`2`) we can similar calculate the second with `1 * 7! <= (1000000 - 2 * 8!)`, `2 * 7! <= (1000000 - 2 * 8!)` ...
+The last thing we have to be aware of is that this method yields us to the "n-th digit of the remaining digits". So if we got the 6th digit for our second calculation its in fact `7`, because we already used `2`.
+
+The program now does exactly these calculations, you can see in the top row the already used digits (they are crossed out).
+
+All in all this program pretty fast - they could really do another version of this problem with bigger numbers.
\ No newline at end of file
diff --git a/www/statics/euler/euler_025.php b/www/statics/euler/euler_025.php
new file mode 100644
index 0000000..42b093f
--- /dev/null
+++ b/www/statics/euler/euler_025.php
@@ -0,0 +1,19 @@
+ 25,
+ 'title' => '1000-digit Fibonacci number',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_025_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_025_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_025_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=025',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-025.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 745055403,
+ 'time' => 116938,
+ 'width' => 123,
+ 'height' => 28,
+ 'value' => 4782,
+];
diff --git a/www/statics/euler/euler_025_code.txt b/www/statics/euler/euler_025_code.txt
new file mode 100644
index 0000000..9d8f1e7
--- /dev/null
+++ b/www/statics/euler/euler_025_code.txt
@@ -0,0 +1,28 @@
+v
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000
+ 00000000000000000000000000000000000000000000000001 00000000000000000000000000000000000000000000000001
+
+>5567***00p"2"10p 230p>v
+> > 00g40p050p>40g1-40p40g10g%"4"+40g10g/1+g"0"-:40g10g%1+40g10g/1+g"0"-50g++ v
+ v< v< |g04p+1/g01g04+1%g01g04+"0"p+1/g01g04+"4"%g01g04+"0"%+55p05/+55:<
+^<|-*+55"d"-g07g00<|-"0"g+1/g01g07+"4"%g01g0730g.@ >70g1+70p ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_025_description.md b/www/statics/euler/euler_025_description.md
new file mode 100644
index 0000000..30f1ef8
--- /dev/null
+++ b/www/statics/euler/euler_025_description.md
@@ -0,0 +1,22 @@
+The Fibonacci sequence is defined by the recurrence relation:
+
+Fn = Fn?1 + Fn?2, where F1 = 1 and F2 = 1.
+
+Hence the first 12 terms will be:
+
+F1 = 1
+F2 = 1
+F3 = 2
+F4 = 3
+F5 = 5
+F6 = 8
+F7 = 13
+F8 = 21
+F9 = 34
+F10 = 55
+F11 = 89
+F12 = 144
+
+The 12th term, F12, is the first term to contain three digits.
+
+What is the first term in the Fibonacci sequence to contain 1000 digits?
\ No newline at end of file
diff --git a/www/statics/euler/euler_025_explanation.md b/www/statics/euler/euler_025_explanation.md
new file mode 100644
index 0000000..1f46b36
--- /dev/null
+++ b/www/statics/euler/euler_025_explanation.md
@@ -0,0 +1,2 @@
+And for like the 5th time i implement an long addition algorithm. On the right side is the current number and on the left side the last number.
+The only interesting thing here is probably that I calculate the next number and move the current to the left in a single cycle.
\ No newline at end of file
diff --git a/www/statics/euler/euler_026.php b/www/statics/euler/euler_026.php
new file mode 100644
index 0000000..00aa93d
--- /dev/null
+++ b/www/statics/euler/euler_026.php
@@ -0,0 +1,19 @@
+ 26,
+ 'title' => 'Reciprocal cycles',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_026_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_026_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_026_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=026',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-026.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 21266126,
+ 'time' => 4477,
+ 'width' => 100,
+ 'height' => 16,
+ 'value' => 983,
+];
diff --git a/www/statics/euler/euler_026_code.txt b/www/statics/euler/euler_026_code.txt
new file mode 100644
index 0000000..af3f047
--- /dev/null
+++ b/www/statics/euler/euler_026_code.txt
@@ -0,0 +1,16 @@
+v
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+####################################################################################################
+
+>"d"00p"}"8*60p080p090p #v v# p+1/g00g04%g00g04g05<
+>60g>:30p>:10p>0\00g%10g00g/v>140p050p>4 0g55+*30g%40p50g1+50p40g00g%40g00g/1+g!|
+ >80g.@ |p01::-1g01p+1< vp08g03p09_v#`g09:-g+1/g00g04%g00g04g05 <
+^_^#p06:-1g06 ># $# ^# < $<
\ No newline at end of file
diff --git a/www/statics/euler/euler_026_description.md b/www/statics/euler/euler_026_description.md
new file mode 100644
index 0000000..933900a
--- /dev/null
+++ b/www/statics/euler/euler_026_description.md
@@ -0,0 +1,15 @@
+A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:
+
+ 1/2 = 0.5
+ 1/3 = 0.(3)
+ 1/4 = 0.25
+ 1/5 = 0.2
+ 1/6 = 0.1(6)
+ 1/7 = 0.(142857)
+ 1/8 = 0.125
+ 1/9 = 0.(1)
+ 1/10 = 0.1
+
+Where 0.1(6) means 0.166666..., and has a 1-digit recurring cycle. It can be seen that 1/7 has a 6-digit recurring cycle.
+
+Find the value of d < 1000 for which 1/d contains the longest recurring cycle in its decimal fraction part.
\ No newline at end of file
diff --git a/www/statics/euler/euler_026_explanation.md b/www/statics/euler/euler_026_explanation.md
new file mode 100644
index 0000000..43734fe
--- /dev/null
+++ b/www/statics/euler/euler_026_explanation.md
@@ -0,0 +1,29 @@
+To calculate the repeating-digit-count we use an algorithm based on the idea of a long division. Here on the example of `1/7`
+
+| Position | Value | Remainder | Note |
+|----------|-------------- |---------------|----------------------------------------|
+| 0 | 0, | 10/7 | `10/7 = 1` **&** `(10%7)*10 = 30` |
+| 1 | 0,1 | 30/7 | `30/7 = 1` **&** `(30%7)*10 = 20` |
+| 2 | 0,13 | 20/7 | `20/7 = 1` **&** `(20%7)*10 = 60` |
+| 3 | 0,132 | 60/7 | `60/7 = 1` **&** `(60%7)*10 = 40` |
+| 4 | 0,1328 | 40/7 | `40/7 = 1` **&** `(40%7)*10 = 50` |
+| 5 | 0,13285 | 50/7 | `50/7 = 1` **&** `(50%7)*10 = 10` |
+| 6 | 0,132857 | 10/7 | **duplicate remainder -> loop closed** |
+
+**=>** RepeatingDigitCount := `6 - 0` = `6`
+
+We use a 1000-field "array" to remember every remainder we already had - as soon as we reach one that is already in use the digits start repeating itself.
+
+For better understanding here the **FindRepeatingDigitCount(int divisor)** algorithm in pseudo-code:
+
+```
+int current = 1;
+int position = 0;
+while(true) {
+ current = (current*10) % divisor;
+ position++;
+
+ if (grid[current] != 0) return position - grid[current];
+ else grid[current] = position;
+}
+```
\ No newline at end of file
diff --git a/www/statics/euler/euler_027.php b/www/statics/euler/euler_027.php
new file mode 100644
index 0000000..761fc52
--- /dev/null
+++ b/www/statics/euler/euler_027.php
@@ -0,0 +1,19 @@
+ 27,
+ 'title' => 'Quadratic primes',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_027_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_027_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_027_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=027',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-027.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 37842282,
+ 'time' => 6240,
+ 'width' => 600,
+ 'height' => 162,
+ 'value' => -59231,
+];
diff --git a/www/statics/euler/euler_027_code.txt b/www/statics/euler/euler_027_code.txt
new file mode 100644
index 0000000..be78b68
--- /dev/null
+++ b/www/statics/euler/euler_027_code.txt
@@ -0,0 +1,17 @@
+v // Project Euler - Problem 12
+
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>"d"6*:10p3"2"*:20p*90p230p5558***40p031pv >" ":03p13pv
+v < _^#`g03g09 <
+>"X"30g:10g%\10g/3+p30g>30g+:90g\` #v_$>30g1+:30p:10g%\10g/3+g" "- |
+ ^p+3/g01\%g01:\" ":< ^ <
+v <
+ v ># v# p07:+1g07< >31p50g11p60g21pv v < @.*g12g11<
+>040g-1+50p260p>0:70p>:*50g70g*60g++:1`| >:10g%\10g/3+g" "-#^_70g:31g`| >50g2+:50p40g`!#v_ >040g-1+50p>60g1+:60p:10g%\10g/3+g" "-!#^_60g40g`!#v_^
+ ^ ># $0 ^# ># $# ^# <# <
\ No newline at end of file
diff --git a/www/statics/euler/euler_027_description.md b/www/statics/euler/euler_027_description.md
new file mode 100644
index 0000000..b0d9b8e
--- /dev/null
+++ b/www/statics/euler/euler_027_description.md
@@ -0,0 +1,21 @@
+Euler discovered the remarkable quadratic formula:
+
+~~~
+n^2 + n + 41
+~~~
+
+It turns out that the formula will produce 40 primes for the consecutive values n = 0 to 39.
+However, when `n = 40`, `402 + 40 + 41 = 40(40 + 1) + 41` is divisible by 41, and certainly when `n = 41`, `41^2 + 41 + 41` is clearly divisible by 41.
+
+The incredible formula `n^2 - 79n + 1601` was discovered, which produces 80 primes for the consecutive values n = 0 to 79. The product of the coefficients, -79 and 1601, is -126479.
+
+Considering quadratics of the form:
+
+~~~
+n^2 + an + b, where |a| < 1000 and |b| < 1000
+~~~
+
+where `|n|` is the modulus/absolute value of n
+e.g. `|11| = 11` and `|-4| = 4`
+
+Find the product of the coefficients, a and b, for the quadratic expression that produces the maximum number of primes for consecutive values of n, starting with `n = 0`.
\ No newline at end of file
diff --git a/www/statics/euler/euler_027_explanation.md b/www/statics/euler/euler_027_explanation.md
new file mode 100644
index 0000000..c942882
--- /dev/null
+++ b/www/statics/euler/euler_027_explanation.md
@@ -0,0 +1,5 @@
+If you looked at the previous problems you probably know what comes now ... (Sieve of Eratosthenes)[http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes].
+To lower the amount of A-B combinations we have to check here are 2 rules I found out:
+
+- `B` must be a (positive) prime, otherwise n=0 wouldn't yield a prime number
+- When `B` is a prime `A` must be uneven. Otherwise for n=0 the resulting number would be even and so not a prime.
\ No newline at end of file
diff --git a/www/statics/euler/euler_028.php b/www/statics/euler/euler_028.php
new file mode 100644
index 0000000..9676f4a
--- /dev/null
+++ b/www/statics/euler/euler_028.php
@@ -0,0 +1,19 @@
+ 28,
+ 'title' => 'Number spiral diagonals',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_028_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_028_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_028_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=028',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-028.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 28514,
+ 'time' => 15,
+ 'width' => 54,
+ 'height' => 2,
+ 'value' => 669171001,
+];
diff --git a/www/statics/euler/euler_028_code.txt b/www/statics/euler/euler_028_code.txt
new file mode 100644
index 0000000..34fe9ff
--- /dev/null
+++ b/www/statics/euler/euler_028_code.txt
@@ -0,0 +1,2 @@
+"d"55+*1+::1-01p*>:01g-:01g-:01g-:01g-:1-#v_>+\:#<_$.@
+X ^p10-2g10 <
\ No newline at end of file
diff --git a/www/statics/euler/euler_028_description.md b/www/statics/euler/euler_028_description.md
new file mode 100644
index 0000000..26508d7
--- /dev/null
+++ b/www/statics/euler/euler_028_description.md
@@ -0,0 +1,11 @@
+Starting with the number 1 and moving to the right in a clockwise direction a 5 by 5 spiral is formed as follows:
+
+ 21 22 23 24 25
+ 20 7 8 9 10
+ 19 6 1 2 11
+ 18 5 4 3 12
+ 17 16 15 14 13
+
+It can be verified that the sum of the numbers on the diagonals is 101.
+
+What is the sum of the numbers on the diagonals in a 1001 by 1001 spiral formed in the same way?
\ No newline at end of file
diff --git a/www/statics/euler/euler_028_explanation.md b/www/statics/euler/euler_028_explanation.md
new file mode 100644
index 0000000..c5f9039
--- /dev/null
+++ b/www/statics/euler/euler_028_explanation.md
@@ -0,0 +1,23 @@
+Let's look ate the diagonal numbers of our 5x5 grid:
+
+|n |info |
+|--|---------------|
+|25|starting number|
+|21| = 25 - **4** |
+|17| = 21 - **4** |
+|13| = 17 - **4** |
+|9 | = 13 - **4** |
+|7 | = 9 - **2** |
+|5 | = 7 - **2** |
+|3 | = 5 - **2** |
+|1 | = 3 - **2** |
+
+You can probably see the pattern here. The rest of the algorithm is simply loop from 1001^2 to 1, subtracting the right amount each round and in the end summing up all numbers.
+
+I have this little code to calculate the sum of stack values until a zero is encountered:
+
+```befunge
+>+\:#<_$
+```
+
+Perhaps it's useful for someone else.
\ No newline at end of file
diff --git a/www/statics/euler/euler_029.php b/www/statics/euler/euler_029.php
new file mode 100644
index 0000000..68cb545
--- /dev/null
+++ b/www/statics/euler/euler_029.php
@@ -0,0 +1,19 @@
+ 29,
+ 'title' => 'Distinct powers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_029_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_029_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_029_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=029',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-029.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 6439429168,
+ 'time' => 1423681,
+ 'width' => 248,
+ 'height' => 59,
+ 'value' => 9183,
+];
diff --git a/www/statics/euler/euler_029_code.txt b/www/statics/euler/euler_029_code.txt
new file mode 100644
index 0000000..3046fea
--- /dev/null
+++ b/www/statics/euler/euler_029_code.txt
@@ -0,0 +1,14 @@
+v
+ 000
+ ###
+ . .
+ .
+ . .
+ ###
+
+> "]M~A~~~~~h!"++++++*+**10p":~+"+*55+0p"d"2*1+20pv
+v < v < "4"< @.g0+55$<
+ v < "4"< > $v v p05/+55p06< v < >-!#v_ v
+>20g"4">80p:0\80gp80g1-:1-#^_$1-:#^_$"dd">80p:80g\20 g>:0\1pv>120g1p40p>050p20g60p>60g1g40g*50g+:55+%60g1p60g1-:#^_$$1-:#v_$0170p>9*70g1g+10g%70g1+:70p20g-1-#^_20g"4">90p30p:30g90gg:| >55+0g1-55+0p$v>30g90g1-:1-#^_$1-:1-#^_@>80g1-:1-#v_$1-:1-#v_^
+ ^_^#!:-1< ^ < >$30g90gp$ > ^
+ ^ <"d" <
\ No newline at end of file
diff --git a/www/statics/euler/euler_029_description.md b/www/statics/euler/euler_029_description.md
new file mode 100644
index 0000000..b3a9523
--- /dev/null
+++ b/www/statics/euler/euler_029_description.md
@@ -0,0 +1,12 @@
+Consider all integer combinations of ab for 2 <= a <= 5 and 2 <= b <= 5:
+
+ 2^2=4, 2^3=8, 2^4=16, 2^5=32
+ 3^2=9, 3^3=27, 3^4=81, 3^5=243
+ 4^2=16, 4^3=64, 4^4=256, 4^5=1024
+ 5^2=25, 5^3=125, 5^4=625, 5^5=3125
+
+If they are then placed in numerical order, with any repeats removed, we get the following sequence of 15 distinct terms:
+
+ 4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125
+
+How many distinct terms are in the sequence generated by ab for 2 <= a <= 100 and 2 <= b <= 100?
\ No newline at end of file
diff --git a/www/statics/euler/euler_029_explanation.md b/www/statics/euler/euler_029_explanation.md
new file mode 100644
index 0000000..140aeeb
--- /dev/null
+++ b/www/statics/euler/euler_029_explanation.md
@@ -0,0 +1,4 @@
+This problem is really not made for Befunge. The numbers become quickly too big to be stored in a 64 bit field, and you need to remember a lot of them.
+
+My solution is probably a bit hacky/cheaty: We calculate the numbers via long multiplication and 200 single fields. Then we calculate a hash of that number and store the hash.
+The *cheaty* part is that I needed to be sure there are no hash collisions in our set of numbers - so I tested it beforehand in a quick C# solution. And on a side note: Its disturbing how easy these problems are in a high-level language after working with Befunge for such a log time :(
\ No newline at end of file
diff --git a/www/statics/euler/euler_030.php b/www/statics/euler/euler_030.php
new file mode 100644
index 0000000..6e665c5
--- /dev/null
+++ b/www/statics/euler/euler_030.php
@@ -0,0 +1,19 @@
+ 30,
+ 'title' => 'Digit fifth powers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_030_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_030_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_030_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=030',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-030.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 51019199,
+ 'time' => 7332,
+ 'width' => 59,
+ 'height' => 8,
+ 'value' => 443839,
+];
diff --git a/www/statics/euler/euler_030_code.txt b/www/statics/euler/euler_030_code.txt
new file mode 100644
index 0000000..e2268c4
--- /dev/null
+++ b/www/statics/euler/euler_030_code.txt
@@ -0,0 +1,8 @@
+v >55+/ v v $$_v#!:-1 <<
+>01>::9::*:***0\>:#<|#\+1\<>9::*:***>:::55+%::*:**\55+/v>|:
+ >$ -#v_^>$>+\:#<_vv/+55\**:*::%+55:<->^
+ ^ +1< $>:55+%::*:**\55+/v+
+ .v/+55\**:*::%+55:<+
+ @>:55+%::*:**\55+/v+
+ v/+55\**:*::%+55:<+
+ >55+%::*:**\55+$++^
\ No newline at end of file
diff --git a/www/statics/euler/euler_030_description.md b/www/statics/euler/euler_030_description.md
new file mode 100644
index 0000000..ff783e7
--- /dev/null
+++ b/www/statics/euler/euler_030_description.md
@@ -0,0 +1,11 @@
+Surprisingly there are only three numbers that can be written as the sum of fourth powers of their digits:
+
+1634 = 1^4 + 6^4 + 3^4 + 4^4
+8208 = 8^4 + 2^4 + 0^4 + 8^4
+9474 = 9^4 + 4^4 + 7^4 + 4^4
+
+As 1 = 14 is not a sum it is not included.
+
+The sum of these numbers is 1634 + 8208 + 9474 = 19316.
+
+Find the sum of all the numbers that can be written as the sum of fifth powers of their digits.
\ No newline at end of file
diff --git a/www/statics/euler/euler_030_explanation.md b/www/statics/euler/euler_030_explanation.md
new file mode 100644
index 0000000..2824ba4
--- /dev/null
+++ b/www/statics/euler/euler_030_explanation.md
@@ -0,0 +1,8 @@
+**Yes**. This is in fact the first program without *put* or *get* instructions. It operates completely on the stack. And that makes it **really** fast.
+
+But *- to be fair -* the algorithm is pretty simple:
+
+First get the upper bound for our later search, we search for a number where `digitcount(9^5 * n) <= n`
+
+After our algorithm calculated that number (I resisted the urge to hard code `354294`) we test every number from 0 to limit and sum the fitting ones (there are only 6).
+`4150`, `4151`, `54748`, `92727`, `93084`, `194979`
\ No newline at end of file
diff --git a/www/statics/euler/euler_031.php b/www/statics/euler/euler_031.php
new file mode 100644
index 0000000..cad55e4
--- /dev/null
+++ b/www/statics/euler/euler_031.php
@@ -0,0 +1,19 @@
+ 31,
+ 'title' => 'Coin sums',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_031_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_031_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_031_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=031',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-031.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 310409597,
+ 'time' => 47970,
+ 'width' => 60,
+ 'height' => 11,
+ 'value' => 73682,
+];
diff --git a/www/statics/euler/euler_031_code.txt b/www/statics/euler/euler_031_code.txt
new file mode 100644
index 0000000..f28e82e
--- /dev/null
+++ b/www/statics/euler/euler_031_code.txt
@@ -0,0 +1,11 @@
+v#########
+ ###
+
+>00000000010p20p30p40p50p60p70p80p90p "d"2* 11p921p031p 0v
+v $<
+ vp0p12:+1g120< >g25**+70g5*+80g2*+90g+v
+>21g0g1+21g0p>21g9- |>10g5"d"**20g2"d"**+"d"3v>:11g\`|
+p >^ ^6+**45g05+*"2"g04+*g0$31g.@ >1-21p ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_031_description.md b/www/statics/euler/euler_031_description.md
new file mode 100644
index 0000000..5612782
--- /dev/null
+++ b/www/statics/euler/euler_031_description.md
@@ -0,0 +1,9 @@
+In England the currency is made up of pound, £, and pence, p, and there are eight coins in general circulation:
+
+1p, 2p, 5p, 10p, 20p, 50p, £1 (100p) and £2 (200p).
+
+It is possible to make £2 in the following way:
+
+1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p
+
+How many different ways can £2 be made using any number of coins?
\ No newline at end of file
diff --git a/www/statics/euler/euler_031_explanation.md b/www/statics/euler/euler_031_explanation.md
new file mode 100644
index 0000000..cb67f15
--- /dev/null
+++ b/www/statics/euler/euler_031_explanation.md
@@ -0,0 +1,9 @@
+The algorithm here enumerates through every possible combination using an approach similar to counting binary:
+
+- Increment the last digit until our total sum is greater 200 (test for every combination if total sum == 200)
+- Then set every field from back to front to zero until you find a non-zero field
+- Set this field also to zero
+- Increment the field before ... repeat
+- Abort the loop when you have used every field
+
+That is probably not the most efficient way, but I optimized this brute-force variant enough that it becomes viable.
\ No newline at end of file
diff --git a/www/statics/euler/euler_032.php b/www/statics/euler/euler_032.php
new file mode 100644
index 0000000..7b3c451
--- /dev/null
+++ b/www/statics/euler/euler_032.php
@@ -0,0 +1,19 @@
+ 32,
+ 'title' => 'Pandigital products',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_032_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_032_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_032_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=032',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-032.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 42123428,
+ 'time' => 7191,
+ 'width' => 166,
+ 'height' => 21,
+ 'value' => 45228,
+];
diff --git a/www/statics/euler/euler_032_code.txt b/www/statics/euler/euler_032_code.txt
new file mode 100644
index 0000000..f42c03b
--- /dev/null
+++ b/www/statics/euler/euler_032_code.txt
@@ -0,0 +1,21 @@
+v
+ $$$$$$$$$
+ ###############################
+
+ vp2\0:<
+>" "> 1-:|
+ v < *"ce"<
+v p01 1$< vp1\0:< >v >v >$v >v >v >$v >v >v >$v v\g1:< >10g:1+10p2pv
+>9"ec"*>80p:80g55+> 1-:| >:55+%:|>:1g!|>1\1p55+/:!| >\:>:55+%:|>:1g!|>1\1p55+/:!| >*:>:55+%:|>:1g!|>1\1p55+/:!| >55+> 1-:|>| >80g1-:5558***-#^_$1-:1-|
+ >$:^ $# $# < ^ $# $# < ^ $# $# $ ^v $<
+v < > > > > $> >$ $00>9-! ^ 1
+ | <0 <*9*3+1*94<
+ vp1\0:< >v >v >$v >v >v >$v >v >v >$v v\g1:< >10g:1+10p2pv
+>"c"49*1+3*9*>80p:80g55+> 1-:| >:55+%:|>:1g!|>1\1p55+/:!| >\:>:55+%:|>:1g!|>1\1p55+/:!| >*:>:55+%:|>:1g!|>1\1p55+/:!| >55+> 1-:|>| >80g1-:"d"-#^_$1-:55+-|
+ >$:^ $# $# < ^ $# $# < ^ $# $# $ ^ $
+ > >#v ># ># #< $> >$ $00>9-! ^
+v < v\< ^ <
+ v -1< v< |:g2:<
+ v ># $# ># v# -1< ^$<
+>" ">80p80g1->70p80g2g:!|>70g2g -| > 70g:1-#^_$80g:2-#^_$0>" "> 1-:| >+#<\:#<_+.@
+ >^ >070g2p^ >$^
\ No newline at end of file
diff --git a/www/statics/euler/euler_032_description.md b/www/statics/euler/euler_032_description.md
new file mode 100644
index 0000000..c8f2913
--- /dev/null
+++ b/www/statics/euler/euler_032_description.md
@@ -0,0 +1,7 @@
+We shall say that an n-digit number is pandigital if it makes use of all the digits 1 to n exactly once; for example, the 5-digit number, 15234, is 1 through 5 pandigital.
+
+The product 7254 is unusual, as the identity, 39 × 186 = 7254, containing multiplicand, multiplier, and product is 1 through 9 pandigital.
+
+Find the sum of all products whose multiplicand/multiplier/product identity can be written as a 1 through 9 pandigital.
+
+*HINT: Some products can be obtained in more than one way so be sure to only include it once in your sum.*
\ No newline at end of file
diff --git a/www/statics/euler/euler_032_explanation.md b/www/statics/euler/euler_032_explanation.md
new file mode 100644
index 0000000..6a3b584
--- /dev/null
+++ b/www/statics/euler/euler_032_explanation.md
@@ -0,0 +1,6 @@
+The main focus here was optimizing the pandigital testing. The rest is just looping over every possible number.
+We can optimize the outer loop a little bit if we look at the possible multiplicands.
+There are only 2 possibilities if we need 9 digits in our calculation:
+
+- 1-digit number * 4-digit number = 4-digit number
+- 2-digit number * 3-digit number = 4-digit number
\ No newline at end of file
diff --git a/www/statics/euler/euler_033.php b/www/statics/euler/euler_033.php
new file mode 100644
index 0000000..9e101fd
--- /dev/null
+++ b/www/statics/euler/euler_033.php
@@ -0,0 +1,19 @@
+ 33,
+ 'title' => 'Digit canceling fractions',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_033_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_033_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_033_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=033',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-033.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 661502,
+ 'time' => 109,
+ 'width' => 67,
+ 'height' => 18,
+ 'value' => 100,
+];
diff --git a/www/statics/euler/euler_033_code.txt b/www/statics/euler/euler_033_code.txt
new file mode 100644
index 0000000..85aec3f
--- /dev/null
+++ b/www/statics/euler/euler_033_code.txt
@@ -0,0 +1,18 @@
+v
+>110p120p"cc" v
+vp09p08 < >80g55+/90g55+/-#v_v
+>90g80g`!#v_>80g55+/| >80g90g55+/*90g80g55+/*-#v_v
+ v < < <
+ >80g55+/90g55+%-#v_v
+ >80g55+/| >80g90g55+/*90g80g55+%*-#v_v
+ @v\p05:< v < < <
+ .>50g%:|: < >80g55+%90g55+/-#v_v
+ ^/\g02$< g>80g55+%| >80g90g55+%*90g80g55+/*-#v_v
+ 0v < < <
+ 2 >80g55+%90g55+%-#v_v
+ g>80g55+%| >80g90g55+%*90g80g55+%*-#v_v
+ 0v < < <
+ 1> v
+ ^ $_v#!-9p08:-1g08<_v#!-9p09:-1g09# ^#<
\ No newline at end of file
diff --git a/www/statics/euler/euler_033_description.md b/www/statics/euler/euler_033_description.md
new file mode 100644
index 0000000..816c3c3
--- /dev/null
+++ b/www/statics/euler/euler_033_description.md
@@ -0,0 +1,7 @@
+The fraction 49/98 is a curious fraction, as an inexperienced mathematician in attempting to simplify it may incorrectly believe that 49/98 = 4/8, which is correct, is obtained by cancelling the 9s.
+
+We shall consider fractions like, 30/50 = 3/5, to be trivial examples.
+
+There are exactly four non-trivial examples of this type of fraction, less than one in value, and containing two digits in the numerator and denominator.
+
+If the product of these four fractions is given in its lowest common terms, find the value of the denominator.
\ No newline at end of file
diff --git a/www/statics/euler/euler_033_explanation.md b/www/statics/euler/euler_033_explanation.md
new file mode 100644
index 0000000..e16fcbb
--- /dev/null
+++ b/www/statics/euler/euler_033_explanation.md
@@ -0,0 +1,6 @@
+This one was relaxing. You can simple iterate through all 8100 cases and test each one in short time.
+Three notable things:
+
+- You can test two fraction `a/b` and `c/d` simple of equality with the formula `a*d == b*c`.
+- This is my compact [GCD algorithm](http://en.wikipedia.org/wiki/Euclidean_algorithm) in befunge (stack -> stack)
+- This is one of the few *real* Befunge-93 programs in this series. (It doesn't violate the [80x25](https://github.com/catseye/Befunge-93/blob/master/doc/Befunge-93.markdown) size rule)
\ No newline at end of file
diff --git a/www/statics/euler/euler_034.php b/www/statics/euler/euler_034.php
new file mode 100644
index 0000000..1395aad
--- /dev/null
+++ b/www/statics/euler/euler_034.php
@@ -0,0 +1,19 @@
+ 34,
+ 'title' => 'Digit factorials',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_034_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_034_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_034_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=034',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-034.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 493980359,
+ 'time' => 80933,
+ 'width' => 45,
+ 'height' => 7,
+ 'value' => 40730,
+];
diff --git a/www/statics/euler/euler_034_code.txt b/www/statics/euler/euler_034_code.txt
new file mode 100644
index 0000000..f5c11fb
--- /dev/null
+++ b/www/statics/euler/euler_034_code.txt
@@ -0,0 +1,7 @@
+v
+>1:00p1*:10p2*:20p3*:30p4*:40p5*:v
+vp110$p09:*9p08:*8p07:*7p06:*6p05<
+ v_v# :-190g7*>::0\>:55+%0g\55+/:#v_>+#<\:#<_+-| +
+ >3-.$@ |:/+55\g0%+55: < >:11g^
+ ^g11< > ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_034_description.md b/www/statics/euler/euler_034_description.md
new file mode 100644
index 0000000..a6d6f94
--- /dev/null
+++ b/www/statics/euler/euler_034_description.md
@@ -0,0 +1,5 @@
+145 is a curious number, as 1! + 4! + 5! = 1 + 24 + 120 = 145.
+
+Find the sum of all numbers which are equal to the sum of the factorial of their digits.
+
+Note: as 1! = 1 and 2! = 2 are not sums they are not included.
\ No newline at end of file
diff --git a/www/statics/euler/euler_034_explanation.md b/www/statics/euler/euler_034_explanation.md
new file mode 100644
index 0000000..6213560
--- /dev/null
+++ b/www/statics/euler/euler_034_explanation.md
@@ -0,0 +1,2 @@
+Not much to say here, we save the factorial values to increase speed and operate almost entirely on the stack (also for speed).
+The rest is brute force. Our upper limit is `9!*7 = 2540160`, because `9!*8` has only 7 digits and so is impossible to be a curious number.
\ No newline at end of file
diff --git a/www/statics/euler/euler_035.php b/www/statics/euler/euler_035.php
new file mode 100644
index 0000000..dccadb0
--- /dev/null
+++ b/www/statics/euler/euler_035.php
@@ -0,0 +1,19 @@
+ 35,
+ 'title' => 'Circular primes',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_035_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_035_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_035_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=035',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-035.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 176748467,
+ 'time' => 27565,
+ 'width' => 2000,
+ 'height' => 516,
+ 'value' => 55,
+];
diff --git a/www/statics/euler/euler_035_code.txt b/www/statics/euler/euler_035_code.txt
new file mode 100644
index 0000000..2278a2c
--- /dev/null
+++ b/www/statics/euler/euler_035_code.txt
@@ -0,0 +1,21 @@
+v // Project Euler - Problem 35
+
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+
+>"d"45**:10p5"d"*:20p*00p230p" ":03p13pv v0 p090<
+v < _^#`g03g00<
+>"X"30g:10g%\10g/3+p30g>30g+:00g\` #v_$>30g1+:30p:10g%\10g/3+g" "-|
+ >90g"= ",,.@ ^p+3/g01\%g01:\" ":< ^ <
+v <
+ ^_v# !-g00p03:+1g03$<0 <
+ v < > v
+>230p>30g::10g%\10g/3+g"X"-#^_:150p1\55+/:!#v_>:2%!#v_:5%!#v_55+/\55+*\50g1+50p:|>$60p:70p>::10g%\10g/3+g" "-| :
+ > >^ |p05:-1g05+*g06%+55 \/+55<
+ >55+70g.,90g1+90p0> $>$ ^
+ > > $^> ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_035_description.md b/www/statics/euler/euler_035_description.md
new file mode 100644
index 0000000..a34e3ad
--- /dev/null
+++ b/www/statics/euler/euler_035_description.md
@@ -0,0 +1,5 @@
+The number, 197, is called a circular prime because all rotations of the digits: 197, 971, and 719, are themselves prime.
+
+There are thirteen such primes below 100: 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, and 97.
+
+How many circular primes are there below one million?
\ No newline at end of file
diff --git a/www/statics/euler/euler_035_explanation.md b/www/statics/euler/euler_035_explanation.md
new file mode 100644
index 0000000..f9386ca
--- /dev/null
+++ b/www/statics/euler/euler_035_explanation.md
@@ -0,0 +1,2 @@
+Thats one big [sieve](http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes), even though not as big as the on in problem 10.
+Here we needed a way to "rotate" a number: `value = value%10 * 10^digitcount + value/10`. The rest is standard befunge stuff and trying to optimize it.
\ No newline at end of file
diff --git a/www/statics/euler/euler_036.php b/www/statics/euler/euler_036.php
new file mode 100644
index 0000000..a222085
--- /dev/null
+++ b/www/statics/euler/euler_036.php
@@ -0,0 +1,19 @@
+ 36,
+ 'title' => 'Double-base palindromes',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_036_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_036_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_036_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=036',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-036.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 969574,
+ 'time' => 172,
+ 'width' => 78,
+ 'height' => 8,
+ 'value' => 872187,
+];
diff --git a/www/statics/euler/euler_036_code.txt b/www/statics/euler/euler_036_code.txt
new file mode 100644
index 0000000..2e933ec
--- /dev/null
+++ b/www/statics/euler/euler_036_code.txt
@@ -0,0 +1,8 @@
+v
+0 v \< v *2\< >:.55+,\ v
+>093194*+**>::>55+*10p:55+%10g+\55+/:#^_$::0>10p:2%10g+\2/:#^_$-!#^_$ v
+ |:-1 <
+v < v \< v *2\< >:.55+,\v
+>93194*+**>::55+/>55+*10p:55+%10g+\55+/:#^_$::0>10p:2%10g+\2/:#^_$-!#^_$ v
+ |:-1 <
+ >"= ",,>+\:#<_+.@
\ No newline at end of file
diff --git a/www/statics/euler/euler_036_description.md b/www/statics/euler/euler_036_description.md
new file mode 100644
index 0000000..4ab1ded
--- /dev/null
+++ b/www/statics/euler/euler_036_description.md
@@ -0,0 +1,5 @@
+The decimal number, 585 = 10010010012 (binary), is palindromic in both bases.
+
+Find the sum of all numbers, less than one million, which are palindromic in base 10 and base 2.
+
+(Please note that the palindromic number, in either base, may not include leading zeros.)
\ No newline at end of file
diff --git a/www/statics/euler/euler_036_explanation.md b/www/statics/euler/euler_036_explanation.md
new file mode 100644
index 0000000..7f715dc
--- /dev/null
+++ b/www/statics/euler/euler_036_explanation.md
@@ -0,0 +1,6 @@
+The *trick* here is that we only need to test 1998 numbers. Because there are only so much base10 palindromes:
+
+- The numbers from `1` to `999` mirrored result into to palindromes `11` to `999999`
+- The numbers from `1` to `999` mirrored at the last digit result into to palindromes `1` to `99999`
+
+Then we only need to test these numbers whether they are also binary palindromes.
\ No newline at end of file
diff --git a/www/statics/euler/euler_037.php b/www/statics/euler/euler_037.php
new file mode 100644
index 0000000..225e625
--- /dev/null
+++ b/www/statics/euler/euler_037.php
@@ -0,0 +1,19 @@
+ 37,
+ 'title' => 'Truncatable primes',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_037_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_037_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_037_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=037',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-037.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 128154558,
+ 'time' => 20717,
+ 'width' => 2000,
+ 'height' => 514,
+ 'value' => 748317,
+];
diff --git a/www/statics/euler/euler_037_code.txt b/www/statics/euler/euler_037_code.txt
new file mode 100644
index 0000000..b074669
--- /dev/null
+++ b/www/statics/euler/euler_037_code.txt
@@ -0,0 +1,19 @@
+v
+
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>"d"45**:10p5"d"*:20p*00p230p" ":03p13pv v075320 p090<
+v < _^#`g03g00<
+>"X"30g:10g%\10g/3+p30g>30g+:00g\` #v_$>30g1+:30p:10g%\10g/3+g" "-|
+ >90g"= ",,.@ ^p+3/g01\%g01:\" ":< ^ <
+v < <
+ v ># ># $# v# -1<
+ $ >v >$\ v < >::.55+,90g+90pv
+>:!#v_70p9> :70g55+*+:00g\`|>::10g%\10g/3+g"X"-#^_::55+\`#v_:55+/1\:!#^_55+/\55+*\v>::10g%\10g/3+g"X"-#v_\:50p%50g55+/\:|>| >\>:1-#^_$^
+ >$"= ",,90g.@ ^ < >$ #^!: #< >$$0 > ^> ^
+ ^1$$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_037_description.md b/www/statics/euler/euler_037_description.md
new file mode 100644
index 0000000..62d14f8
--- /dev/null
+++ b/www/statics/euler/euler_037_description.md
@@ -0,0 +1,5 @@
+The number 3797 has an interesting property. Being prime itself, it is possible to continuously remove digits from left to right, and remain prime at each stage: 3797, 797, 97, and 7. Similarly we can work from right to left: 3797, 379, 37, and 3.
+
+Find the sum of the only eleven primes that are both truncatable from left to right and right to left.
+
+*NOTE: 2, 3, 5, and 7 are not considered to be truncatable primes.*
\ No newline at end of file
diff --git a/www/statics/euler/euler_037_explanation.md b/www/statics/euler/euler_037_explanation.md
new file mode 100644
index 0000000..d158754
--- /dev/null
+++ b/www/statics/euler/euler_037_explanation.md
@@ -0,0 +1,2 @@
+The approach for this problem is to first iterate through the left-truncatable primes and test if these are right-truncatable. All with the help of our trusty companion the *sieve of Eratosthenes*.
+Tricky was that the generation of left-truncatable primes, my original algorithm was recursive and I had to transform it to an iterative one for befunge.
\ No newline at end of file
diff --git a/www/statics/euler/euler_038.php b/www/statics/euler/euler_038.php
new file mode 100644
index 0000000..4abdb46
--- /dev/null
+++ b/www/statics/euler/euler_038.php
@@ -0,0 +1,19 @@
+ 38,
+ 'title' => 'Pandigital multiples',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_038_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_038_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_038_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=038',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-038.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 3567967,
+ 'time' => 624,
+ 'width' => 169,
+ 'height' => 6,
+ 'value' => 932718654,
+];
diff --git a/www/statics/euler/euler_038_code.txt b/www/statics/euler/euler_038_code.txt
new file mode 100644
index 0000000..b596db8
--- /dev/null
+++ b/www/statics/euler/euler_038_code.txt
@@ -0,0 +1,8 @@
+v#########
+v######### v <# p145<
+ ######### v +1< v < v < vp2\0:< >v >v >$v v\g2:<
+>"ec"*31p>241p>01-1>:31g*\:41g-#^_$>\10p01-\>:55+%\55+/:#^_$>10g55+*+10p:1+#^_$10g\:1+#v_$:55+> 1-:| >:55+%:|>:2g!|>1\2p55+/:!| >55+> 1-:|>#v_$41g1-:41p1-#^_31g1-:31p|
+ ^ \< $>$:^ $# $# > $0>9-!\$ ^ >. @ ,,,,, "RORRE"<
+ v <
+02>:31g*\:41g-#^_31g*
\ No newline at end of file
diff --git a/www/statics/euler/euler_038_description.md b/www/statics/euler/euler_038_description.md
new file mode 100644
index 0000000..0712e81
--- /dev/null
+++ b/www/statics/euler/euler_038_description.md
@@ -0,0 +1,11 @@
+Take the number 192 and multiply it by each of 1, 2, and 3:
+
+ 192 × 1 = 192
+ 192 × 2 = 384
+ 192 × 3 = 576
+
+By concatenating each product we get the 1 to 9 pandigital, 192384576. We will call 192384576 the concatenated product of 192 and (1,2,3)
+
+The same can be achieved by starting with 9 and multiplying by 1, 2, 3, 4, and 5, giving the pandigital, 918273645, which is the concatenated product of 9 and (1,2,3,4,5).
+
+What is the largest 1 to 9 pandigital 9-digit number that can be formed as the concatenated product of an integer with (1,2, ... , n) where n > 1?
\ No newline at end of file
diff --git a/www/statics/euler/euler_038_explanation.md b/www/statics/euler/euler_038_explanation.md
new file mode 100644
index 0000000..5baef47
--- /dev/null
+++ b/www/statics/euler/euler_038_explanation.md
@@ -0,0 +1,2 @@
+Not much to say here. I needed to implement a way of merging numbers and a way of testing for pandigitals (we already did that in problem 32).
+Then we start from `9999` downward, because bigger numbers will always lead to 10 digits or more.
\ No newline at end of file
diff --git a/www/statics/euler/euler_039.php b/www/statics/euler/euler_039.php
new file mode 100644
index 0000000..091ce7c
--- /dev/null
+++ b/www/statics/euler/euler_039.php
@@ -0,0 +1,19 @@
+ 39,
+ 'title' => 'Integer right triangles',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_039_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_039_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_039_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=039',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-039.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 3815878,
+ 'time' => 827,
+ 'width' => 72,
+ 'height' => 6,
+ 'value' => 840,
+];
diff --git a/www/statics/euler/euler_039_code.txt b/www/statics/euler/euler_039_code.txt
new file mode 100644
index 0000000..6a8755f
--- /dev/null
+++ b/www/statics/euler/euler_039_code.txt
@@ -0,0 +1,6 @@
+v
+>010p020p630p"d"55+*90p050p30g3/70p v
+ vp07/3g03p050 p03+2<
+v ># v# p07-1< >10p30g20pv
+>30g::270g*-*\70g-2*%#^_50g1+50p>70g:2-#^_$50g:10g`#^_$ >30g:90g-|
+ > $^$ < @.g02$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_039_description.md b/www/statics/euler/euler_039_description.md
new file mode 100644
index 0000000..ae27e6c
--- /dev/null
+++ b/www/statics/euler/euler_039_description.md
@@ -0,0 +1,5 @@
+If p is the perimeter of a right angle triangle with integral length sides, {a,b,c}, there are exactly three solutions for p = 120.
+
+{20,48,52}, {24,45,51}, {30,40,50}
+
+For which value of p ? 1000, is the number of solutions maximised?
\ No newline at end of file
diff --git a/www/statics/euler/euler_039_explanation.md b/www/statics/euler/euler_039_explanation.md
new file mode 100644
index 0000000..1956fb2
--- /dev/null
+++ b/www/statics/euler/euler_039_explanation.md
@@ -0,0 +1,2 @@
+We have the two formulas `a^2 + b^2 = c^2` and `a + b + c = p`. We can insert the second in the first and get `b = p*(p-2a) / 2*(p-a)` and `c = p-(b+a)`.
+The we just go through all possible values for a and p and test if b is an integer. Then we search for the value of p with the most possible values of a.
\ No newline at end of file
diff --git a/www/statics/euler/euler_040.php b/www/statics/euler/euler_040.php
new file mode 100644
index 0000000..3042abd
--- /dev/null
+++ b/www/statics/euler/euler_040.php
@@ -0,0 +1,19 @@
+ 40,
+ 'title' => 'Champernowne\'s constant',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_040_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_040_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_040_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=040',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-040.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 1486,
+ 'time' => 16,
+ 'width' => 69,
+ 'height' => 7,
+ 'value' => 210,
+];
diff --git a/www/statics/euler/euler_040_code.txt b/www/statics/euler/euler_040_code.txt
new file mode 100644
index 0000000..ec9434e
--- /dev/null
+++ b/www/statics/euler/euler_040_code.txt
@@ -0,0 +1,7 @@
+v
+>01:55+*:55+*:55+*:55+*:55+*:55+*130p v
+ v <
+>110p120p>:10g920g**`!#v_10g920g**-10g1+10p20g55+*20p^>v <
+ >30g.@ >1-:10g/20g+\ 10g%10g\-1-:|>\55+/\1-:#^_v
+ $ $ > :^
+^_^#: <# p03*g03%+55$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_040_description.md b/www/statics/euler/euler_040_description.md
new file mode 100644
index 0000000..efc8c21
--- /dev/null
+++ b/www/statics/euler/euler_040_description.md
@@ -0,0 +1,9 @@
+An irrational decimal fraction is created by concatenating the positive integers:
+
+0.123456789101112131415161718192021...
+
+It can be seen that the 12th digit of the fractional part is 1.
+
+If d(n) represents the nth digit of the fractional part, find the value of the following expression.
+
+d(1) × d(10) × d(100) × d(1000) × d(10000) × d(100000) × d(1000000)
\ No newline at end of file
diff --git a/www/statics/euler/euler_040_explanation.md b/www/statics/euler/euler_040_explanation.md
new file mode 100644
index 0000000..268ec5a
--- /dev/null
+++ b/www/statics/euler/euler_040_explanation.md
@@ -0,0 +1,26 @@
+This one is really great - I came up with an O(log n) algorithm (crazy fast) for determining the n-th digit.
+First I tested it in LinqPad, so here the C# code for the algorithm:
+
+```csharp
+public int digitAt(int pos) {
+ int digitcount = 1;
+ int digitvalue = 1;
+
+ // Get DigitCount of current number
+ while(pos > digitvalue * 9 * digitcount) {
+ pos -= digitvalue * 9 * digitcount;
+ digitcount++;
+ digitvalue *= 10;
+ }
+
+ // current number and digit-position in number
+ int value = digitvalue + (pos - 1)/digitcount;
+ int digit = digitcount - (pos - 1)%digitcount - 1;
+
+ return getInternalDigit(value, digit);
+}
+
+public int getInternalDigit(int value, int digit) {
+ return (value / (int)Math.Pow(10, digit)) % 10;
+}
+```
\ No newline at end of file
diff --git a/www/statics/euler/euler_041.php b/www/statics/euler/euler_041.php
new file mode 100644
index 0000000..c15c42e
--- /dev/null
+++ b/www/statics/euler/euler_041.php
@@ -0,0 +1,19 @@
+ 41,
+ 'title' => 'Pandigital prime',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_041_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_041_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_041_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=041',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-041.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 83726,
+ 'time' => 31,
+ 'width' => 40,
+ 'height' => 17,
+ 'value' => 7652413,
+];
diff --git a/www/statics/euler/euler_041_code.txt b/www/statics/euler/euler_041_code.txt
new file mode 100644
index 0000000..c7fddf6
--- /dev/null
+++ b/www/statics/euler/euler_041_code.txt
@@ -0,0 +1,17 @@
+vXXXXXX
+vXXXXXX
+$
+>7 12p 0>:0\1p::"1"+v
+ |-g21:+1p0\ <
+v p231$<
+ >32g1gv
+ >32g2%| vp24<>2g1g1+32gv
+>32g:1g`| >0 ^^3p0g23p0<1
+^ >032g1pv>42g0g32g0g42g^p
+^p23+1g23 < vp230<
+ v6:-1g26*+ 55<0p26g21< @.<
+ >2p0g"0"-+62g| $
+ # >:>302pv >:02g2-:*` !|
+ $ >!\2% +|%p20+1:g20:<
+ ^`2::< $
+ ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_041_description.md b/www/statics/euler/euler_041_description.md
new file mode 100644
index 0000000..d14bac3
--- /dev/null
+++ b/www/statics/euler/euler_041_description.md
@@ -0,0 +1,3 @@
+We shall say that an n-digit number is pandigital if it makes use of all the digits 1 to n exactly once. For example, 2143 is a 4-digit pandigital and is also prime.
+
+What is the largest n-digit pandigital prime that exists?
diff --git a/www/statics/euler/euler_041_explanation.md b/www/statics/euler/euler_041_explanation.md
new file mode 100644
index 0000000..9bd1ba9
--- /dev/null
+++ b/www/statics/euler/euler_041_explanation.md
@@ -0,0 +1,8 @@
+Perhaps you remember from elementary school that numbers with a digit sum divisible by three is also divisible by three (an so not a prime).
+So our number can't be 9 digits long (digit sum = `45`) nor 8 (digit sum = `36`). Our next best try is a 7-digit palindrome.
+
+With the [QuickPerm algorithm](http://www.quickperm.org/) we generate all the permutations and test them for their primality.
+This time we don't use a prime sieve, the numbers are just too big and it's faster with a simple naive prime test.
+
+The rest is just implementation.
+But the resulting code looks imho pretty nice because it really uses the four directions of befunge and often intersects with itself, even though I think that doesn't make it more readable.
\ No newline at end of file
diff --git a/www/statics/euler/euler_042.php b/www/statics/euler/euler_042.php
new file mode 100644
index 0000000..5827171
--- /dev/null
+++ b/www/statics/euler/euler_042.php
@@ -0,0 +1,19 @@
+ 42,
+ 'title' => 'Coded triangle numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_042_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_042_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_042_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=042',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-042.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 526637,
+ 'time' => 406,
+ 'width' => 112,
+ 'height' => 1788,
+ 'value' => 162,
+];
diff --git a/www/statics/euler/euler_042_code.txt b/www/statics/euler/euler_042_code.txt
new file mode 100644
index 0000000..8287a65
--- /dev/null
+++ b/www/statics/euler/euler_042_code.txt
@@ -0,0 +1,20 @@
+ v ################################################################################
+ ################################################################################
+A ################################################################################
+ABILITY ################################################################################
+ABLE ################################################################################
+ABOUT v <
+ABOVE > 1"/&"*+00p>"P":10p 5:20p *30p 050p 260p^
+ABSENCE
+ABSOLUTELY >50g1+:50p :1+*2/ "0"\ :10g%" "+\10g/p v
+ACADEMIC |`\g03 /2*+1: +1g05<
+ACCEPT
+ACCESS >070p0>70g60gg:" "-!#v_"@"-+v
+ACCIDENT ^p07+1g07 $# <
+ACCOMPANY |-g00p06+1:g06pg06*39<
+ACCORDING
+ACCOUNT >260p 0 >93*60gg:10g%" "+\10g/g"0"-!v
+ACHIEVE |-g00 p06+1:g06 +<
+ACHIEVEMENT @.<
+...
+...
\ No newline at end of file
diff --git a/www/statics/euler/euler_042_description.md b/www/statics/euler/euler_042_description.md
new file mode 100644
index 0000000..4f3790a
--- /dev/null
+++ b/www/statics/euler/euler_042_description.md
@@ -0,0 +1,7 @@
+The nth term of the sequence of triangle numbers is given by `t(n) = 0.5 * n(n+1)`; so the first ten triangle numbers are:
+
+`1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ...`
+
+By converting each letter in a word to a number corresponding to its alphabetical position and adding these values we form a word value. For example, the word value for SKY is `19 + 11 + 25 = 55 = t(10)`. If the word value is a triangle number then we shall call the word a triangle word.
+
+Using words.txt (right click and 'Save Link/Target As...'), a 16K text file containing nearly two-thousand common English words, how many are triangle words?
diff --git a/www/statics/euler/euler_042_explanation.md b/www/statics/euler/euler_042_explanation.md
new file mode 100644
index 0000000..3ae8eb5
--- /dev/null
+++ b/www/statics/euler/euler_042_explanation.md
@@ -0,0 +1,7 @@
+Similar to problem 22 this is not quite befunge-friendly due to enormous input size.
+But otherwise it wasn't hard, I create for every word the word value and count the triangle numbers in it.
+
+Two little tricks:
+
+ - I cached the triangle numbers from 1 to 400 (biggest possible word value is 364 because the longest word is 14 letters)
+ - to count the triangle numbers just add the boolean results of the `isTriangle` function. Because true is `1` and false is `0` this results equals the number of triangle numbers.
diff --git a/www/statics/euler/euler_043.php b/www/statics/euler/euler_043.php
new file mode 100644
index 0000000..efdcbef
--- /dev/null
+++ b/www/statics/euler/euler_043.php
@@ -0,0 +1,19 @@
+ 43,
+ 'title' => 'Sub-string divisibility',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_043_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_043_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_043_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=043',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-043.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 821317,
+ 'time' => 140,
+ 'width' => 68,
+ 'height' => 23,
+ 'value' => 16695334890,
+];
diff --git a/www/statics/euler/euler_043_code.txt b/www/statics/euler/euler_043_code.txt
new file mode 100644
index 0000000..883a844
--- /dev/null
+++ b/www/statics/euler/euler_043_code.txt
@@ -0,0 +1,23 @@
+vXXXXXXXXX
+vXXXXXXXXX
+
+>902p012p9>:0\1pv
+ |\-1: <
+>12g55+, #$ " =",, . @ vp20<
+|`9g20 < < <
+ >$0v > v >002g0g"0"-1p v
+>02g0g"0"-:9`| >:22p55+-| >22g1g #v_ 02g0g"9"`!#^_ ## v
+ >1+^ >0|-9p22+1:g22 02g0g"9"`!#v_ ^ +
+ >002g0g"0"-1p"X"02g0p^ 1
+>#v_002p 032p0>:0g"0"-32g55v>12p> ^g
+ >02g9-!02g8-!02g7-!++v |-9\+1:p23+*+<+ 2
+ v < >$32g:.55+,12g^ 0
+ >02g6-70g"0"-55+*80g"0"-+55+*90g"0"-+89+%+!v>++#^_02g0g"9"`!#v_^
+ v!+%+58+-"0"g08*+55+-"0"g07*+55-"0"g06-5g20<+v"X"p1-"0"g0g200<#
+ >02g4-50g"0"-55+*60g"0"-+55+*70g"0"-+47+%+!v+>02g0p02g1+02p ^
+ v!+%+70+-"0"g06*+55+-"0"g05*+55-"0"g04-3g20<+
+ >02g2-30g"0"-55+*40g"0"-+55+*50g"0"-+05+%+!v+
+ v!+%+30+-"0"g04*+55+-"0"g03*+55-"0"g02-1g20<+
+ >02g0-10g"0"-55+*20g"0"-+55+*30g"0"-+02+%+!>^
\ No newline at end of file
diff --git a/www/statics/euler/euler_043_description.md b/www/statics/euler/euler_043_description.md
new file mode 100644
index 0000000..a3435b0
--- /dev/null
+++ b/www/statics/euler/euler_043_description.md
@@ -0,0 +1,13 @@
+The number, `1406357289`, is a 0 to 9 pandigital number because it is made up of each of the digits 0 to 9 in some order, but it also has a rather interesting sub-string divisibility property.
+
+Let d1 be the 1st digit, d2 be the 2nd digit, and so on. In this way, we note the following:
+
+ - d2d3d4 =406 is divisible by 2
+ - d3d4d5 =063 is divisible by 3
+ - d4d5d6 =635 is divisible by 5
+ - d5d6d7 =357 is divisible by 7
+ - d6d7d8 =572 is divisible by 11
+ - d7d8d9 =728 is divisible by 13
+ - d8d9d10=289 is divisible by 17
+
+Find the sum of all 0 to 9 pandigital numbers with this property.
\ No newline at end of file
diff --git a/www/statics/euler/euler_043_explanation.md b/www/statics/euler/euler_043_explanation.md
new file mode 100644
index 0000000..4e00d4e
--- /dev/null
+++ b/www/statics/euler/euler_043_explanation.md
@@ -0,0 +1,10 @@
+While trying to optimize this problem I found that you don't even need a program to solve this.
+You can easily get the result by calculating it on paper.
+I have documented my calculations in my [Github repo](https://github.com/Mikescher/Project-Euler_Befunge).
+But I wanted an program to do this (where you could for example change the constraints), so I wrote this.
+
+The code here was a tight fit into the Befunge-93 80x25 grid, not because of some big data structures but because of a lot of code.
+
+Here we generate all combinations from the last digit to the first, we significantly limit the amount of possible combinations by checking the constraints for every number.
+For example we are at `???????410`, we then don't need to evaluate the first 7 digits because constraint 7 is violated (divisibility of d_789 by 17).
+This way instead of evaluating `3,628,800` possibilities we only have to look at `1702`.
\ No newline at end of file
diff --git a/www/statics/euler/euler_044.php b/www/statics/euler/euler_044.php
new file mode 100644
index 0000000..df971ff
--- /dev/null
+++ b/www/statics/euler/euler_044.php
@@ -0,0 +1,19 @@
+ 44,
+ 'title' => 'Pentagon numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_044_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_044_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_044_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=044',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-044.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 1509045439,
+ 'time' => 258993,
+ 'width' => 60,
+ 'height' => 11,
+ 'value' => 5482660,
+];
diff --git a/www/statics/euler/euler_044_code.txt b/www/statics/euler/euler_044_code.txt
new file mode 100644
index 0000000..fe156a2
--- /dev/null
+++ b/www/statics/euler/euler_044_code.txt
@@ -0,0 +1,11 @@
+>v%%% %%%% > v
+v06p09:/2*-1*3:p06::+1:70p:3*1 v # >0v>vv p03+g03*2:p04-\g04+g03:<
+v <3 pp2# v/4 < >:30g+40g`! |
+1# > 4**1+:0^ 40>0g>:40g`#^_>:|:/4p03/2g03< $
+>-:|^6-p08:/2*-< # >^ >30g2/30p4/^ >$30g:*-30g\ |
+ 8 >$$ ^v030:+1**46+g09g08 ># !# # _^
+ >::**::**8*20p1 ^v>vv p03+g03*2:p04-\g04+g03:<@.-g08g0 9<
+ pp2# v/4 < >:30g+40g`! | ^5%6 <$
+ 40>0g>:40g`#^_>:|:/4p03/2g03< >$ ^
+ >^ >30g2/30p4/^ >$30g:*-30g\ #^_6%5-#^_^
\ No newline at end of file
diff --git a/www/statics/euler/euler_044_description.md b/www/statics/euler/euler_044_description.md
new file mode 100644
index 0000000..4fbdea7
--- /dev/null
+++ b/www/statics/euler/euler_044_description.md
@@ -0,0 +1,7 @@
+Pentagonal numbers are generated by the formula, `Pn=n(3n-1)/2`. The first ten pentagonal numbers are:
+
+> 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, ...
+
+It can be seen that `P4 + P7 = 22 + 70 = 92 = P8`. However, their difference, `70 - 22 = 48`, is not pentagonal.
+
+Find the pair of pentagonal numbers, Pj and Pk, for which their sum and difference are pentagonal and `D = | Pk - Pj |` is minimised; what is the value of D?
diff --git a/www/statics/euler/euler_044_explanation.md b/www/statics/euler/euler_044_explanation.md
new file mode 100644
index 0000000..911d973
--- /dev/null
+++ b/www/statics/euler/euler_044_explanation.md
@@ -0,0 +1,8 @@
+My first attempt at this problem took over 5 hours to compute and had a complexity of O(n^3).
+
+The problem is that you need a square root to inverse the pentagonal formula and Befunge has no square root function.
+So I needed to implement my own version of integer square roots in Befunge (see [wikipedia](http://en.wikipedia.org/wiki/Methods_of_computing_square_roots)).
+The program is still not really fast but it's good that I managed to speed it up to a time where you can execute it without waiting the whole night.
+
+Also this program is nicely compact, by the time I'm writing this my Befunge interpreter [BefunExec](http://www.mikescher.de/programs/view/BefunGen) has gotten a display of all possible paths a program can take.
+And if you look at the graph of this program, it looks pretty interesting...
\ No newline at end of file
diff --git a/www/statics/euler/euler_045.php b/www/statics/euler/euler_045.php
new file mode 100644
index 0000000..83d4770
--- /dev/null
+++ b/www/statics/euler/euler_045.php
@@ -0,0 +1,19 @@
+ 45,
+ 'title' => 'Triangular, pentagonal, and hexagonal',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_045_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_045_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_045_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=045',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-045.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 25312679,
+ 'time' => 3494,
+ 'width' => 48,
+ 'height' => 6,
+ 'value' => 1533776805,
+];
diff --git a/www/statics/euler/euler_045_code.txt b/www/statics/euler/euler_045_code.txt
new file mode 100644
index 0000000..6dfd991
--- /dev/null
+++ b/www/statics/euler/euler_045_code.txt
@@ -0,0 +1,6 @@
+v >v
+>8::**::**8*:*20pv0v>vv p03+g03*2:p01-\g01+g03:<
+v +"l#"<3pp2# v/4 < >:30g+10g`! |
+>1+::2*1-*64**v 010>0g>:10g`#^_>:|:/4p03/2g03<
+^ < $<>1+:^>^ >30g2/30p4/^ >$30g:*-v
+@.*-1*2:_^#!_^#! -5%6g03<
\ No newline at end of file
diff --git a/www/statics/euler/euler_045_description.md b/www/statics/euler/euler_045_description.md
new file mode 100644
index 0000000..5ecc68c
--- /dev/null
+++ b/www/statics/euler/euler_045_description.md
@@ -0,0 +1,11 @@
+Triangle, pentagonal, and hexagonal numbers are generated by the following formulae:
+
+ Name | Formula | Numbers
+------------|----------------------|-------------------------
+Triangle | `T_{n} = n(n+1)/2` | `1, 3, 6, 10, 15, ...`
+Pentagonal | `P_{n} = n(3n-1)/2` | `1, 5, 12, 22, 35, ...`
+Hexagonal | `H_{n} = n(2n-1)` | `1, 6, 15, 28, 45, ...`
+
+It can be verified that `T285 = P165 = H143 = 40755`.
+
+Find the next triangle number that is also pentagonal and hexagonal.
\ No newline at end of file
diff --git a/www/statics/euler/euler_045_explanation.md b/www/statics/euler/euler_045_explanation.md
new file mode 100644
index 0000000..953370d
--- /dev/null
+++ b/www/statics/euler/euler_045_explanation.md
@@ -0,0 +1,8 @@
+This problem is very similar to the previous one. We iterate through all Pentagonal numbers (starting at P_144) and test the numbers if they are hexagonal.
+
+The test for hexagonal numbers is the same as in Problem-44, but we have to expand the iSquare function for int64 numbers ([20] is now 2^60 instead of 2^30).
+
+The major trick is that we only need to test for the hexagonal property. Because all hexagonal numbers are also Triangle numbers.
+Think about it, a Hexagon has six edges and a Triangle three, so every Hexagonal contains two triangles.
+
+`H_{n} == T_{2*n}`
\ No newline at end of file
diff --git a/www/statics/euler/euler_046.php b/www/statics/euler/euler_046.php
new file mode 100644
index 0000000..7fe6124
--- /dev/null
+++ b/www/statics/euler/euler_046.php
@@ -0,0 +1,19 @@
+ 46,
+ 'title' => 'Goldbach\'s other conjecture',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_046_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_046_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_046_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=046',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-046.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 77542913,
+ 'time' => 13899,
+ 'width' => 200,
+ 'height' => 57,
+ 'value' => 5777,
+];
diff --git a/www/statics/euler/euler_046_code.txt b/www/statics/euler/euler_046_code.txt
new file mode 100644
index 0000000..bcc81d4
--- /dev/null
+++ b/www/statics/euler/euler_046_code.txt
@@ -0,0 +1,12 @@
+v
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+ >2 v >0v>vv p09+g09*2:p07-\g07+g09:<
+ v p+1/g01\%g01:\"O"< $v < 9@pp8# v/4 < >:90g+70g`! |
+>"d"2*:10p"2":20p*40p230pv >030p 350p >50g2+:50p::10g%\10g/1+g" "-#^_^>1+:50g-!#v_::10g%\10g/1+g" "-!#^_:50g\-2/:0^.70>0g>:70g`#^_>:|:/4p09/2g09<
+vp08*8**::**::8p11p10:" "< _^#`g03g04< ^ > ^>^ >90g2/90p4/^ >$90g:*-#v_v
+>"X"30g:10g%\10g/1+p30g>30g+:40g\` #v_$>30g1+:30p:10g%\10g/1+g" "-| $ ^ <
+ ^p+1/g01\%g01:\" ":< ^ < ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_046_description.md b/www/statics/euler/euler_046_description.md
new file mode 100644
index 0000000..d7a16e7
--- /dev/null
+++ b/www/statics/euler/euler_046_description.md
@@ -0,0 +1,12 @@
+It was proposed by Christian Goldbach that every odd composite number can be written as the sum of a prime and twice a square.
+
+`9 = 7 + 2 * 1^2`
+`15 = 7 + 2 * 2^2`
+`21 = 3 + 2 * 3^2`
+`25 = 7 + 2 * 3^2`
+`27 = 19 + 2 * 2^2`
+`33 = 31 + 2 * 1^2`
+
+It turns out that the conjecture was false.
+
+What is the smallest odd composite that cannot be written as the sum of a prime and twice a square?
\ No newline at end of file
diff --git a/www/statics/euler/euler_046_explanation.md b/www/statics/euler/euler_046_explanation.md
new file mode 100644
index 0000000..c4a00b0
--- /dev/null
+++ b/www/statics/euler/euler_046_explanation.md
@@ -0,0 +1,5 @@
+I really missed my [sieve of erastothenes](http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes). There were really a few problems without primes in a row.
+
+In this problem we go through all primes `i`, search through all smaller primes `j` were `(i-j)/2` is a quadratic number. If you can't find one, this falsifies the theorem.
+
+Also we use the code from problem 46 to calculate the integer square root.
\ No newline at end of file
diff --git a/www/statics/euler/euler_047.php b/www/statics/euler/euler_047.php
new file mode 100644
index 0000000..d14a3b3
--- /dev/null
+++ b/www/statics/euler/euler_047.php
@@ -0,0 +1,19 @@
+ 47,
+ 'title' => 'Distinct primes factors',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_047_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_047_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_047_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=047',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-047.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 3227917351,
+ 'time' => 537798,
+ 'width' => 400,
+ 'height' => 518,
+ 'value' => 134043,
+];
diff --git a/www/statics/euler/euler_047_code.txt b/www/statics/euler/euler_047_code.txt
new file mode 100644
index 0000000..5dfc48f
--- /dev/null
+++ b/www/statics/euler/euler_047_code.txt
@@ -0,0 +1,21 @@
+v
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+
+>"d"4 *:10p5"d"*:20p*00p230p" ":03p13pv >040p030p>>30g1+:30p:10g%\10g/3+g"X"-#v_30g40g:1+40p:10g%\10g/3+p00g30g`#v_v
+v < _^#`g03g00<^ < < 0
+>"X"30g:10g%\10g/3+p30g>30g+:00g\` #v_$>30g1+:30p:10g%\10g/3+g" "-|v p+3/g01\%g01:-1g04<
+ ^p+3/g01\%g01:\" ":< ^ <>1>:0:40p50p>:40g:10g%\10g/3+g% #v_40g:10g%\10gv
+ + |!`\g+3/g01\%g01:p04:+1g04:$50g4-#v_080p:::4+60p70p3->:70g- #v_80g1+:80p4-#v_3-.$@
+ ^ < |-g06:+1< <
+ ^ $< >:0:40p50p>:40g:10g%\10g/3+g% #v_40g:10g%\10gv
+ ^ <|!`\g+3/g01\%g01:p04:+1g04:$50g4-#v_80g1+80p v
+ | -4g08 <
+ >3-.$@ >080p:70g\`|
+ ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_047_description.md b/www/statics/euler/euler_047_description.md
new file mode 100644
index 0000000..b0fad65
--- /dev/null
+++ b/www/statics/euler/euler_047_description.md
@@ -0,0 +1,14 @@
+
+
+The first two consecutive numbers to have two distinct prime factors are:
+~~~
+14 = 2 × 7
+15 = 3 × 5
+~~~
+The first three consecutive numbers to have three distinct prime factors are:
+~~~
+644 = 2 × 2 × 7 × 23
+645 = 3 × 5 × 43
+646 = 2 × 17 × 19.
+~~~
+Find the first four consecutive integers to have four distinct prime factors. What is the first of these numbers?
diff --git a/www/statics/euler/euler_047_explanation.md b/www/statics/euler/euler_047_explanation.md
new file mode 100644
index 0000000..a5286c8
--- /dev/null
+++ b/www/statics/euler/euler_047_explanation.md
@@ -0,0 +1,16 @@
+This is a relative straightforward problem:
+
+ - First we calculate all primes from `0` to `200 000` with a sieve of Eratosthenes.
+ - Then we collect all primes side by side together in the top rows, because we only need to iterate through the primes and never actually do a prime test.
+ - If we iterate through all the primes and test the divisibility we can calculate the number of *distinct prime*
+ - So we check every fourth number (if it has 4 distinct prime factors).
+ - If we found one, we test the 7 surrounding numbers for 4 adjacent matches (the first one we print out and exit the program)
+
+This program is not that fast, even I did multiple performance improvements:
+
+ - We pre-calculate the primes with an sieve of Eratosthenes
+ - We generate an easily iterable array of primes
+ - We test only every 4th number - this reduces the number of distinct prime factor calculations greatly
+ - We early exit the "test 7 surrounding numbers" method, when we reached a point where there can't be a positive result
+
+But still, it's mostly optimised brute force and not pretty fast.
\ No newline at end of file
diff --git a/www/statics/euler/euler_048.php b/www/statics/euler/euler_048.php
new file mode 100644
index 0000000..520f710
--- /dev/null
+++ b/www/statics/euler/euler_048.php
@@ -0,0 +1,19 @@
+ 48,
+ 'title' => 'Self powers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_048_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_048_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_048_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=048',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-048.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 11530541,
+ 'time' => 3728,
+ 'width' => 37,
+ 'height' => 3,
+ 'value' => 9110846700,
+];
diff --git a/www/statics/euler/euler_048_code.txt b/www/statics/euler/euler_048_code.txt
new file mode 100644
index 0000000..bdf5838
--- /dev/null
+++ b/www/statics/euler/euler_048_code.txt
@@ -0,0 +1,3 @@
+v v0p01**< >:30p::>20p\1-: #v_$$v
+5>8#<"}"* #*>:| ^%g01*g02:\< 2
+>5+:::*:*: ^^-># $# .# @#1g03%g01+g0<
\ No newline at end of file
diff --git a/www/statics/euler/euler_048_description.md b/www/statics/euler/euler_048_description.md
new file mode 100644
index 0000000..040ff8e
--- /dev/null
+++ b/www/statics/euler/euler_048_description.md
@@ -0,0 +1,3 @@
+The series, 1^1 + 2^2 + 3^3 + ... + 10^10 = 10405071317.
+
+Find the last ten digits of the series, 1^1 + 2^2 + 3^3 + ... + 1000^1000.
\ No newline at end of file
diff --git a/www/statics/euler/euler_048_explanation.md b/www/statics/euler/euler_048_explanation.md
new file mode 100644
index 0000000..80e2e26
--- /dev/null
+++ b/www/statics/euler/euler_048_explanation.md
@@ -0,0 +1,7 @@
+I like the occasionally really easy problems between the others. It's like a little break sometimes.
+
+The "trick" here is to understand the modulo operator. If you have `(a + b) % c` you can also write `a%c + b%c`.
+And also you can write `(a * b)%c` as `(a%c) * (b%c)`.
+
+So all we do is calculate the sum kinda normally, but we do modulo `10^10` after each step (every addition and multiplication).
+We guarantee this way that out numbers never exceed the range of an 64bit integer.
\ No newline at end of file
diff --git a/www/statics/euler/euler_049.php b/www/statics/euler/euler_049.php
new file mode 100644
index 0000000..82ac66c
--- /dev/null
+++ b/www/statics/euler/euler_049.php
@@ -0,0 +1,19 @@
+ 49,
+ 'title' => 'Prime permutations',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_049_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_049_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_049_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=049',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-049.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 378809,
+ 'time' => 124,
+ 'width' => 66,
+ 'height' => 8,
+ 'value' => 296962999629,
+];
diff --git a/www/statics/euler/euler_049_code.txt b/www/statics/euler/euler_049_code.txt
new file mode 100644
index 0000000..a743bda
--- /dev/null
+++ b/www/statics/euler/euler_049_code.txt
@@ -0,0 +1,8 @@
+v?>:55+%2+\55+/:5v>"Z%"v>+\55+/:55v>v v 0`*"ce":+*"Z%"$<
+" :v55:/+55\+2%+5<\ v<*2v+55\+2%+<:v>$:.48*,"Z%"*+:.48*,"Z%"*+. @
+( :>+%2+\55+/2+***^ 01+%/>* -#v_-!|:|< #
+% v5:/+55\+2%+55::g<:1+2* v <">::2%!#v_v >10g\%!#v_:10g2/`|
+" >5+%2+\55+/:55v p05+* $ ve#< v%3:>#<#^ #< > v :
+* +v***+2/+55\+2%+< ^<5>^ $ c` > !#^_10p7:^:+6_^#%\g01-2<
+7 1>\"Z%"*+:55+%2+\55+/:^ v <"*^ $$$<
+>+^ < >^
\ No newline at end of file
diff --git a/www/statics/euler/euler_049_description.md b/www/statics/euler/euler_049_description.md
new file mode 100644
index 0000000..de76a6a
--- /dev/null
+++ b/www/statics/euler/euler_049_description.md
@@ -0,0 +1,9 @@
+
+
+The arithmetic sequence, `1487, 4817, 8147`, in which each of the terms increases by `3330`, is unusual in two ways:
+ - (i) each of the three terms are prime, and,
+ - (ii) each of the 4-digit numbers are permutations of one another.
+
+There are no arithmetic sequences made up of three 1-, 2-, or 3-digit primes, exhibiting this property, but there is one other 4-digit increasing sequence.
+
+What 12-digit number do you form by concatenating the three terms in this sequence?
diff --git a/www/statics/euler/euler_049_explanation.md b/www/statics/euler/euler_049_explanation.md
new file mode 100644
index 0000000..9d7fa5a
--- /dev/null
+++ b/www/statics/euler/euler_049_explanation.md
@@ -0,0 +1,10 @@
+This could be the first problem with prime numbers but without a prime sieve.
+We iterate through the numbers from `1488` to `3340` and search for palindromes.
+To speed up the palindrome calculation we calculate the product of each digit plus two and compare the product of our three numbers.
+This is only an approximation, but a rather good one. In tested the numbers from `0` to `100 000` and there were **zero** failures.
+
+So now we've got the numbers where `digit_product(p) == digit_product(p+3330) == digit_product(p+6660)` (in fact there are only 40 of these).
+We then use a simple primality test to check if all three numbers are prime.
+The primality test is basically a port of the [wikipedia](http://en.wikipedia.org/wiki/Primality_test) version to befunge. Wit it we only have to do `n/6` divisions to test a number `n` for primality.
+
+All in all tis leads to a fast, small and not very grid-intensive program (Only one field is used, *and only as a temporary storage to swap three values*).
\ No newline at end of file
diff --git a/www/statics/euler/euler_050.php b/www/statics/euler/euler_050.php
new file mode 100644
index 0000000..96c5019
--- /dev/null
+++ b/www/statics/euler/euler_050.php
@@ -0,0 +1,19 @@
+ 50,
+ 'title' => 'Consecutive prime sum',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_050_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_050_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_050_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=050',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-050.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 180368553,
+ 'time' => 30904,
+ 'width' => 2000,
+ 'height' => 512,
+ 'value' => 997651,
+];
diff --git a/www/statics/euler/euler_050_code.txt b/www/statics/euler/euler_050_code.txt
new file mode 100644
index 0000000..f0a2cc1
--- /dev/null
+++ b/www/statics/euler/euler_050_code.txt
@@ -0,0 +1,17 @@
+v // Project Euler - Problem 50
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>"d"45**:10p5"d"*:20p*00p230p" ":03p13pv >040p030p>>30g1+:30p:10g%\10g/1+g"X"-#v_30g40g:1+40p:10g%\10g/1+p00g30g`#v_v
+v < _^#`g03g00<^ < < 0
+>"X"30g:10g%\10g/1+p30g>30g+:00g\` #v_$>30g1+:30p:10g%\10g/1+g" "-|v p091 p080 p07-10 p060 p+1/g01\%g01:p04:-1g04<
+ >90g"= ",,.@ ^p+1/g01\%g01:\" ":< ^ 70g1+:70p:10g%\10g/1+g80g+:00g\`#^_70g1-70p$v
+vp05g04g08 < <<
+>:50g\50g:10g%\10g/1+g-#v_$. @ >80g60g1-:10g%\10g/1+g+70g:10g%\10g/1+g-v^p09*-10g09$060g90g+`#v_90g1-| >:00g\`!#v_8 0p90g:60g+60p70g+70p^>90g1- |
+ >80g60g:10g%\10g/1+g-70g1+:10g%\10g/1+g+^ $ ^p06+1g06p08-g+1/g01\% g01:g06g08<
+ > > ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_050_description.md b/www/statics/euler/euler_050_description.md
new file mode 100644
index 0000000..1e58a9d
--- /dev/null
+++ b/www/statics/euler/euler_050_description.md
@@ -0,0 +1,9 @@
+The prime 41, can be written as the sum of six consecutive primes:
+
+> 41 = 2 + 3 + 5 + 7 + 11 + 13
+
+This is the longest sum of consecutive primes that adds to a prime below one-hundred.
+
+The longest sum of consecutive primes below one-thousand that adds to a prime, contains 21 terms, and is equal to 953.
+
+Which prime, below one-million, can be written as the sum of the most consecutive primes?
\ No newline at end of file
diff --git a/www/statics/euler/euler_050_explanation.md b/www/statics/euler/euler_050_explanation.md
new file mode 100644
index 0000000..0704e15
--- /dev/null
+++ b/www/statics/euler/euler_050_explanation.md
@@ -0,0 +1,39 @@
+My first approach here was a simple brute force algorithm, but that one was *far* too slow. So I needed an more intelligent algorithm. And I have to say the one I came up is pretty quick and I like the concept that lies behind it.
+
+First I calculated the primes from `0` to `1 000 000`.
+
+Next I calculated the maximum chain *(starting by the first prime `2`)* with a sum less than one million.
+
+Now think of all the primes laid down in an array side by side:
+
+**1)** We move our chain from left to right until the sum exceeds one million (the movement is a really cheap operation: take the previous sum, subtract the most left prime and add the new prime from the reight side).
+
+**2)** Then we shorten the chain length by one as we remove the most left prime.
+
+**3)** After that we do the movement back wards (from right to left) until we end up at the left end of our prime array.
+
+**4)** Then we again shorten the chain *(this time by removing the right tail)* and start over again (by moving right).
+
+**X)** In every step we test if the current sum is a prime number and if so we print it and terminate the program.
+
+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+OOOOOOOOOOOOO // the prime array
+#####OOOOOOOO // our chain
+O#####OOOOOOO // move right
+OO#####OOOOOO
+OOO#####OOOOO // until sum > MAX_VALUE
+OOOO####OOOOO // shorten left
+OOO####OOOOOO // move left
+OO####OOOOOOO
+O####OOOOOOOO
+####OOOOOOOOO // until left side is hit
+###OOOOOOOOOO // shorten right
+O###OOOOOOOOO // repeat until prime is found
+~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
+
+This algorithm works because we first test every possibility with maximum chain length, and then every with length = `maximum - 1` and so on and so on. So the first prime that we find is from the longest possible chain.
+
+There are two nice things about this algorithm:
+
+ - We don't need to calculate an extreme amount of prime sums. The step from the sum of one chain to the next is literally only an addition and an subtraction
+ - Because we start with the longest chain and reduce its length in every step, the first prime we find is directly our optimal result.
\ No newline at end of file
diff --git a/www/statics/euler/euler_051.php b/www/statics/euler/euler_051.php
new file mode 100644
index 0000000..0c3fe89
--- /dev/null
+++ b/www/statics/euler/euler_051.php
@@ -0,0 +1,19 @@
+ 51,
+ 'title' => 'Prime digit replacements',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_051_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_051_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_051_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=051',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-051.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 802550671,
+ 'time' => 113896,
+ 'width' => 78,
+ 'height' => 20,
+ 'value' => 121313,
+];
diff --git a/www/statics/euler/euler_051_code.txt b/www/statics/euler/euler_051_code.txt
new file mode 100644
index 0000000..b01127a
--- /dev/null
+++ b/www/statics/euler/euler_051_code.txt
@@ -0,0 +1,20 @@
+"c"02p v >02g1+::02p 2%!#v_5%!#v_312p>12g1+:12p27*-!#v_022pv> v
+############## >#|v#-*8"}"g20< $ ^ < >1#0|
+OOO OO OOO # ^ @# ># ^# < < <^_^#<1>v
+############## >22g1+:22p3-!^2#
+110001#??????# > ^ <
+101001#??????# > ^v24 pg21+7\+"0"%+55g24:>#<: !#v_ v g+
+100101#??????# >g55+/42p> ^ |-"0"gg21: -1#$>1-:7+12gvgg
+011001#??????# >82g8-| @ ^6<|:\-"0"g <"2
+010101#??????# $ >72g.^ >$ ^>$#<55+*+55+v02
+010011#??????# vp29g22p281 $_v# `/2g25:_^#%\g25< v_v# %2: ^ ># ^#>#<:3%v >+55+*+v >^
+001011#??????# $ >2-52g\%!#^_6+:^:7p25_^# < ^ p27:<
+000111#??????# >92g1+92pv v_v# :>#<:42g55+%"0"+\7+92g4+p42 v
+############## |-9g29< >602g42p>1 -:12gg"0"-| ^ ^ ^ $< v6$< >:92g"0"+\7+92g4+p^
+v_v# `/2g25:_v# %\g25< v_v# %2<>>1-:7+92g4v>v
+8 v ># ^#>#<:3%v: |:\-"0"g+ <+5
+2 >:2-52g\%!#v_6+:^:7p25_^# <+ >$55+*+55+*^5
+>g1+82p >$ ^ ^ *+55+*+55+*+<
\ No newline at end of file
diff --git a/www/statics/euler/euler_051_description.md b/www/statics/euler/euler_051_description.md
new file mode 100644
index 0000000..751311b
--- /dev/null
+++ b/www/statics/euler/euler_051_description.md
@@ -0,0 +1,5 @@
+By replacing the 1st digit of the 2-digit number *3, it turns out that six of the nine possible values:`13`, `23`, `43`, `53`, `73`, and `83`, are all prime.
+
+By replacing the 3rd and 4th digits of `56**3` with the same digit, this 5-digit number is the first example having seven primes among the ten generated numbers, yielding the family: `56003`, `56113`, `56333`, `56443`, `56663`, `56773`, and `56993`. Consequently `56003`, being the first member of this family, is the smallest prime with this property.
+
+Find the smallest prime which, by replacing part of the number (not necessarily adjacent digits) with the same digit, is part of an eight prime value family.
\ No newline at end of file
diff --git a/www/statics/euler/euler_051_explanation.md b/www/statics/euler/euler_051_explanation.md
new file mode 100644
index 0000000..9b3db91
--- /dev/null
+++ b/www/statics/euler/euler_051_explanation.md
@@ -0,0 +1,9 @@
+This is effectively an optimized implementation of [this algorithm](http://www.mathblog.dk/project-euler-51-eight-prime-family/).
+You can see the ten patterns on the left side and beside them the area were we build our numbers.
+
+So what we do is iterate through the numbers from `100` to `1 000`, through the ten patterns and through the digits `0`, `1` and `2`.
+In each iteration we generate the number (from value, pattern and digit) and test for it primeness (with a simple [primality test](http://en.wikipedia.org/wiki/Primality_test) - no prime sieve).
+If we found a prime we count the number of primes in it's family and if this count is eight we print the generated number and exit.
+
+This program is not the fastest, because I check all the primes "manually" and not with an prime sieve each iteration takes quite a time.
+But I wanted this to fit into the befunge-93 size restrictions, and even without a sieve the execution time is OK - for a befunge program.
\ No newline at end of file
diff --git a/www/statics/euler/euler_052.php b/www/statics/euler/euler_052.php
new file mode 100644
index 0000000..ebee2c5
--- /dev/null
+++ b/www/statics/euler/euler_052.php
@@ -0,0 +1,19 @@
+ 52,
+ 'title' => 'Permuted multiples',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_052_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_052_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_052_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=052',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-052.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 18887060,
+ 'time' => 2917,
+ 'width' => 45,
+ 'height' => 6,
+ 'value' => 142857,
+];
diff --git a/www/statics/euler/euler_052_code.txt b/www/statics/euler/euler_052_code.txt
new file mode 100644
index 0000000..bae572c
--- /dev/null
+++ b/www/statics/euler/euler_052_code.txt
@@ -0,0 +1,6 @@
+55+>v>v>5+/>::103p55+*>55+/ :#v_$212pv
+XX :6/5 > ::103p55+*^p30*g30+2%+55:< :
+XX 0:1: v$_v#!: /+55<*+55p311* :55+%2+13g*13p^ >:12g^
+ >^>^>^ >3g03g- #v_12g1+:12p7-|
+ ^*+55$_^#!`\g11:+1$< @$$.<
\ No newline at end of file
diff --git a/www/statics/euler/euler_052_description.md b/www/statics/euler/euler_052_description.md
new file mode 100644
index 0000000..f735f05
--- /dev/null
+++ b/www/statics/euler/euler_052_description.md
@@ -0,0 +1,3 @@
+It can be seen that the number, `125874`, and its double, `251748`, contain exactly the same digits, but in a different order.
+
+Find the smallest positive integer, x, such that 2x, 3x, 4x, 5x, and 6x, contain the same digits.
diff --git a/www/statics/euler/euler_052_explanation.md b/www/statics/euler/euler_052_explanation.md
new file mode 100644
index 0000000..419e88e
--- /dev/null
+++ b/www/statics/euler/euler_052_explanation.md
@@ -0,0 +1,7 @@
+To be a permutation all six numbers have to have the same digit count. So `digitcount(x) == digitcount(x*6)`.
+
+This for each number of digits only given for the numbers from `10^n` to `10/6 * 10^n`.
+We perform the permutation check with an modified version of the algorithm used in problem-49 *(product of all digits plus two)*.
+But we generalise the code to work with every number of digits.
+
+And because we greatly limited the amount of numbers to search and the permutation test is pretty fast this is all we need to do (except run the code).
\ No newline at end of file
diff --git a/www/statics/euler/euler_053.php b/www/statics/euler/euler_053.php
new file mode 100644
index 0000000..867ccea
--- /dev/null
+++ b/www/statics/euler/euler_053.php
@@ -0,0 +1,19 @@
+ 53,
+ 'title' => 'Combinatoric selections',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_053_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_053_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_053_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=053',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-053.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 372790,
+ 'time' => 125,
+ 'width' => 80,
+ 'height' => 7,
+ 'value' => 4075,
+];
diff --git a/www/statics/euler/euler_053_code.txt b/www/statics/euler/euler_053_code.txt
new file mode 100644
index 0000000..c95f563
--- /dev/null
+++ b/www/statics/euler/euler_053_code.txt
@@ -0,0 +1,7 @@
+v ### ####################################################
+ ####################################################
+>190p191p020p130pv >40g9+30g2%!g40g8+30g2%!g+vv!g!%2g03+9g04`**<
+>30g:"d"-!#v_1+:30p2/40p>30g40g2*>-| >:40g9+30g2%p"}}@"^
+^ >#<$ #<20g.@ >40g8+30g2%!g2* ^>$40g9+1-30g2%!g!v
+ >30g40g2* -^v _v#!_v#!_v#!<
+ ^ _^#!p04:-1g04 123, 124, 125, 134, 135, 145, 234, 235, 245, and 345
+
+In combinatorics, we use the notation, `C(5,3) = 10`.
+
+In general, `C(n,r) = n! / (r!(n?r)!)` ,where `r <= n, n! = n * (n?1) * ... * 3 * 2 * 1`, and `0! = 1`.
+
+It is not until `n = 23`, that a value exceeds one-million: `C(23,10) = 1144066`.
+
+How many, not necessarily distinct, values of `C(n,r)`, for `1 <= n <= 100`, are greater than one-million?
\ No newline at end of file
diff --git a/www/statics/euler/euler_053_explanation.md b/www/statics/euler/euler_053_explanation.md
new file mode 100644
index 0000000..c3a6fbb
--- /dev/null
+++ b/www/statics/euler/euler_053_explanation.md
@@ -0,0 +1,44 @@
+*That* is the kind of problem I really like. There is a lot of depth in the solution and a proper algorithm solves this in no time.
+
+The algorithm idea here is that we use the properties of [Pascal's Triangle](http://en.wikipedia.org/wiki/Pascal%27s_triangle).
+As you probably know this triangle starts at its top with a `1`. Then every cell is calculated as the sum of the two cells above it.
+
+~~~
+cell[y][x] = cell[y-1][x-1] + cell[y-1][x]
+~~~
+
+
+
+When we calculate `C(n, r)` this is nothing more than the number at row *n* and column *r*.
+
+So what we do is build [Pascal's Triangle](http://en.wikipedia.org/wiki/Pascal%27s_triangle) up to a height of one-hundred and look at the cells with values greater than one million.
+The obvious problem is that the numbers grow extremely big, and sooner or later *(probably sooner)* the numbers will overflow. So what we do is use a little trick:
+As soon as a cell is over `1 000 000` we mark her *(= put a zero in that cell)*. When we create a new cell out of its two parents we check if one of the parents has the mark *(= is zero)* and then the children gets also marked. Because if one of the parents (or both) is over one million then all of its children will also be over one million.
+
+Another "trick" is that we don't need to remember the whole triangle, only the current and the last row are important. So we have two "arrays" each representing a row and after every cycle the two change roles. The *lastRow* becomes the *currentRow* and vice versa. In Befunge we can do this simply by placing the two arrays on top of each other and accessing them with `y = row%2` or `y = (row+1)%2`.
+
+There is one last optimisation I have done and this one will allow us to fit our program in the 80x25 Befunge-93 size restrictions.
+The triangle is symmetric and we can only look at one half of it. But we have to be aware of the fact that now every found number counts two times (one for each side) **except** it's exactly in the middle. ALso if we want to calculate the value of the middle cell we can't take the value of the right parent (this one does not exist / was never calculated), but because of it's symmetric properties we can just take the left one two times.
+
+~~~
+for(int row = 2; row <= NMAX; row++)
+ for(int col = (row/2); col > 0; col--)
+ {
+ if (2*col == row)
+ matrix[row % 2][col] = matrix[(row + 1) % 2][col - 1] * 2;
+ else
+ matrix[row % 2][col] = matrix[(row + 1) % 2][col] + matrix[(row + 1) % 2][col - 1];
+
+
+ if (matrix[row % 2][col] > 1000000 || matrix[(row + 1) % 2][col] == 0 || matrix[(row + 1) % 2][col - 1] == 0)
+ {
+ count += (2 * col == row) ? 1 : 2;
+ matrix[row % 2][col] = 0;
+ }
+ }
+~~~
+
+
+> **Tip:**
+>
+> Run this code with [BefunExec](https://github.com/Mikescher/BefunExec) on the 50kHz speed setting - it looks quite cool in action.
\ No newline at end of file
diff --git a/www/statics/euler/euler_054.php b/www/statics/euler/euler_054.php
new file mode 100644
index 0000000..caa111c
--- /dev/null
+++ b/www/statics/euler/euler_054.php
@@ -0,0 +1,19 @@
+ 54,
+ 'title' => 'Poker hands',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_054_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_054_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_054_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=054',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-054.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 5949695,
+ 'time' => 2543,
+ 'width' => 118,
+ 'height' => 1009,
+ 'value' => 376,
+];
diff --git a/www/statics/euler/euler_054_code.txt b/www/statics/euler/euler_054_code.txt
new file mode 100644
index 0000000..dfdf5d5
--- /dev/null
+++ b/www/statics/euler/euler_054_code.txt
@@ -0,0 +1,34 @@
+>096p"~"8*1+04p906p036p 116p v
+
+###############
+
+$
+$ $
+$$ $$$$$ $
+$$
+
+8C TS KC 9H 4S 7D 2S 5D 3S AC
+5C AD 5D AC 9C 7C 5H 8D TD KS
+3H 7H 6S KC JS QH TD JC 2D 8S
+TH 8H 5C QS TC 9H 4D JC KS JS >"A"v
+7C 5H KC QH JD AS KH 4C AD 4S >36g06gg36g3%|
+5H KS 9C 7D 9H 8D 3S 5D 5C AH >"0"-55+\:89+-!#v_:39*-!#v_:"!"-!#v_ :892*+-!#v_:66*-!#v_\$v
+6H 4H 5C 3H 2H 3S QH 5S 6S AS > v>$1+ 0>$1+ 0>$1+ 0>$1+ 0>$1+v
+TD 8C 4H 7C TC KC 4C 3H 7S KS vp63+1g63 ># #< v
+7C 9C 6D KD 3H 4C QS QC AC KH |-g40g60< |-*65g63 pg60-/3:g63<
+JC 6S 5H 2H 2D KD 9D 7C AS JS 8 ^p60+1g60p630 pg60-/3:g63" "<
+AD QH TH 9D 8H TS 6D 3S AS AC 0 v 61g64p64+**"23"!!+++!-g65**+"$~ll"!-g65*9*93!-g<
+2H 4S 5C 5S TC KC JD 6C TS 3C g v$_v#!\-1: <6 v<
+QD AS 6H JS 2C 3D 9H KC 4H 8S 7 > 3*> :2g:1-*48*8**46g+46p ::2g\1+2g*!!35g+35p^5 1g
+KD 8S 9S 7C 2S 3S 6D 6S 4H KC 6 p 5>46g66g+76g35**+35g4-!"A'"*5+*+7::*:**56g-!48*^ +2
+3C 8C 2D 7D 4D 9S 4S QH 4H JD p > v p v_v#!\-1:< v _v#!%+55p63:+2g63p2g5016g!:16p|p61:!g61<>#5 88+> :0\2p^ # >g6v 5
+3D KH QD 6C 6S AD AS 8H 2H QS >06g1+06pv^ 3 >$$ 16g55+*36p046p156p066p076p>36g06gg05p3v5v6< 0
+6S 8D 4C 8S 6C QH TC 6D 7D 9D vg71g70 _v#-g40g60`96g+96v>07g17g`96 g+:96p.@ >*56p05g66g` |>05g2g!#^_05g76g`|
+3C QS 2S 4H JH 3D 2D TD 8S 9H > ^ >^ ^ <
+5H QS 8S 6D 3C 8C JD AS 7H 7D
+. . .
+. . .
+. . .
+. . .
\ No newline at end of file
diff --git a/www/statics/euler/euler_054_description.md b/www/statics/euler/euler_054_description.md
new file mode 100644
index 0000000..2005b29
--- /dev/null
+++ b/www/statics/euler/euler_054_description.md
@@ -0,0 +1,45 @@
+
+
+In the card game poker, a hand consists of five cards and are ranked, from lowest to highest, in the following way:
+
+* High Card: Highest value card.
+* One Pair: Two cards of the same value.
+* Two Pairs: Two different pairs.
+* Three of a Kind: Three cards of the same value.
+* Straight: All cards are consecutive values.
+* Flush: All cards of the same suit.
+* Full House: Three of a kind and a pair.
+* Four of a Kind: Four cards of the same value.
+* Straight Flush: All cards are consecutive values of same suit.
+* Royal Flush: Ten, Jack, Queen, King, Ace, in same suit.
+
+The cards are valued in the order:
+2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace.
+
+If two players have the same ranked hands then the rank made up of the highest value wins; for example, a pair of eights beats a pair of fives (see example 1 below). But if two ranks tie, for example, both players have a pair of queens, then highest cards in each hand are compared (see example 4 below); if the highest cards tie then the next highest cards are compared, and so on.
+
+Consider the following five hands dealt to two players:
+
+Hand | Player 1 | Player 2 | Winner
+-------|------------------|---------------------|------------
+ | | |
+1 | 5H 5C 6S 7S KD | 2C 3S 8S 8D TD | Player 2
+ | Pair of Fives | Pair of Eights |
+ | | |
+2 | 5D 8C 9S JS AC | 2C 5C 7D 8S QH | Player 1
+ | Highest card Ace | Highest card Queen |
+ | | |
+3 | 2D 9C AS AH AC | 3D 6D 7D TD QD | Player 2
+ | Three Aces | Flush with Diamonds |
+ | | |
+4 | 4D 6S 9H QH QC | 3D 6D 7H QD QS | Player 1
+ | Pair of Queens | Pair of Queens |
+ | Highest card Nine| Highest card Seven |
+ | | |
+5 | 2H 2D 4C 4D 4S | 3C 3D 3S 9S 9D | Player 1
+ | Full House | Full House |
+ | With Three Fours | with Three Threes |
+
+The file, poker.txt, contains one-thousand random hands dealt to two players. Each line of the file contains ten cards (separated by a single space): the first five are Player 1's cards and the last five are Player 2's cards. You can assume that all hands are valid (no invalid characters or repeated cards), each player's hand is in no specific order, and in each hand there is a clear winner.
+
+How many hands does Player 1 win?
diff --git a/www/statics/euler/euler_054_explanation.md b/www/statics/euler/euler_054_explanation.md
new file mode 100644
index 0000000..ee20ccf
--- /dev/null
+++ b/www/statics/euler/euler_054_explanation.md
@@ -0,0 +1,68 @@
+Yep, I *hate* this problem.
+Not only is there an enormous amount of input data that makes our program huge in size.
+But it contains a lot of different cases, rules and logic that needs be represented in our program
+
+But none the less I tried to come up with an compact algorithm for scoring a set of cards
+
+~~~
+Get(@"https://projecteuler.net/project/resources/p054_poker.txt")
+ .Where(p => GetScore(p.deck_1) > GetScore(p.deck_2))
+ .Count()
+ .Dump();
+~~~
+
+~~~
+int GetScore(Card[] cards) {
+ List SUMS = new List{ H*H*H*H*H, C*C*C*C*C, S*S*S*S*S, D*D*D*D*D };
+
+ int[] array = new int[15];
+ int score = 0;
+ int flushSum = 1;
+ int highCard = 0;
+ int highGroup = 0;
+ int straightIndex = 0;
+
+ foreach(Card c in cards) {
+ highCard = Math.Max(highCard, c.value);
+ flushSum *= c.suit;
+ if (array[c.value] > 0)
+ highGroup = Math.Max(highGroup, c.value);
+ array[c.value]++;
+ }
+
+ for(int i = 1; i < 15; i++)
+ {
+ score += (array[i]-1)*(array[i])*256;
+
+ if (array[i] > 0 && array[i-1] > 0)
+ straightIndex++;
+ }
+ score += highCard;
+ score += highGroup * 15;
+
+ if (straightIndex == 4)
+ score += 2540;
+ if (SUMS.Contains(flushSum))
+ score += 2550;
+
+ return score;
+}
+~~~
+
+The different values are carefully crafted in such a way, that you can compare the score of two hands and get the winner
+
+ Card | Calculation | Score
+---------------------|----------------|---------------------------------------------
+High Card | {0-14} * [1] | = {0-14}
+High Card (in Group) | {0-14} * [15] | = {0-210}
+One Pair | 2 * [256] | = 512 *(+ HighCard)* *(+ HighGroup)*
+Two Pairs | 4 * [256] | = 1024 *(+ HighCard)* *(+ HighGroup)*
+Three of a Kind | 6 * [256] | = 1536 *(+ HighCard)* *(+ HighGroup)*
+Straight | [2540] | = 2540 *(+ HighCard)* *(+ HighGroup)*
+Flush | [2550] | = 2550 *(+ HighCard)* *(+ HighGroup)*
+Full House | 10 * [256] | = 2560 *(+ HighCard)* *(+ HighGroup)*
+Four of a Kind | 12 * [256] | = 3072 *(+ HighCard)* *(+ HighGroup)*
+Straight Flush | [2540] + [2550]| = 5090 *(+ HighCard)* *(+ HighGroup)*
+Royal Flush | [2540] + [2550]| = 5090 *(+ HighCard)* *(+ HighGroup)*
+
+One last side note: A **royal flush** is not really a independent rank. Because of the "highest card in the rank" rule a royal flush is always better than a straight flush (because the highest card is an ace)
diff --git a/www/statics/euler/euler_055.php b/www/statics/euler/euler_055.php
new file mode 100644
index 0000000..260415d
--- /dev/null
+++ b/www/statics/euler/euler_055.php
@@ -0,0 +1,19 @@
+ 55,
+ 'title' => 'Lychrel numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_055_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_055_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_055_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=055',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-055.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 10470329,
+ 'time' => 2215,
+ 'width' => 56,
+ 'height' => 5,
+ 'value' => 249,
+];
diff --git a/www/statics/euler/euler_055_code.txt b/www/statics/euler/euler_055_code.txt
new file mode 100644
index 0000000..e57ca88
--- /dev/null
+++ b/www/statics/euler/euler_055_code.txt
@@ -0,0 +1,5 @@
+v v-1\+g02<
+0 v/+55\+g01\p01%+< $ v/+55\+g01\p01%+<
+>"}P"*>::0\>:!#v_\55+*\:55 ^>:!#v_\::0\>:!#v_\55+*\:55 ^
+ >$ .@ >$+38* #v ^# < |-p02:$<
+ ^_^#!:-1 <\+1\$$<^$$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_055_description.md b/www/statics/euler/euler_055_description.md
new file mode 100644
index 0000000..850a261
--- /dev/null
+++ b/www/statics/euler/euler_055_description.md
@@ -0,0 +1,19 @@
+If we take 47, reverse and add, `47 + 74 = 121`, which is palindromic.
+
+Not all numbers produce palindromes so quickly. For example,
+
+~~~
+349 + 943 = 1292,
+1292 + 2921 = 4213
+4213 + 3124 = 7337
+~~~
+
+That is, 349 took three iterations to arrive at a palindrome.
+
+Although no one has proved it yet, it is thought that some numbers, like `196`, never produce a palindrome. A number that never forms a palindrome through the reverse and add process is called a Lychrel number. Due to the theoretical nature of these numbers, and for the purpose of this problem, we shall assume that a number is Lychrel until proven otherwise. In addition you are given that for every number below ten-thousand, it will either (i) become a palindrome in less than fifty iterations, or, (ii) no one, with all the computing power that exists, has managed so far to map it to a palindrome. In fact, `10677` is the first number to be shown to require over fifty iterations before producing a palindrome: `4668731596684224866951378664` (53 iterations, 28-digits).
+
+Surprisingly, there are palindromic numbers that are themselves Lychrel numbers; the first example is `4994`.
+
+How many Lychrel numbers are there below ten-thousand?
+
+> NOTE: Wording was modified slightly on 24 April 2007 to emphasise the theoretical nature of Lychrel numbers.
diff --git a/www/statics/euler/euler_055_explanation.md b/www/statics/euler/euler_055_explanation.md
new file mode 100644
index 0000000..958fa31
--- /dev/null
+++ b/www/statics/euler/euler_055_explanation.md
@@ -0,0 +1,2 @@
+Not much to say about this one. I reuse the isPalindrome code from P-36 and bruteforce through all the numbers.
+I think it would be really useful to cache the intermediate results - but our befunge space is too small for such data structures :/
\ No newline at end of file
diff --git a/www/statics/euler/euler_056.php b/www/statics/euler/euler_056.php
new file mode 100644
index 0000000..ce321c5
--- /dev/null
+++ b/www/statics/euler/euler_056.php
@@ -0,0 +1,19 @@
+ 56,
+ 'title' => 'Powerful digit sum',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_056_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_056_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_056_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=056',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-056.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 62461749,
+ 'time' => 13915,
+ 'width' => 75,
+ 'height' => 11,
+ 'value' => 972,
+];
diff --git a/www/statics/euler/euler_056_code.txt b/www/statics/euler/euler_056_code.txt
new file mode 100644
index 0000000..847cb4b
--- /dev/null
+++ b/www/statics/euler/euler_056_code.txt
@@ -0,0 +1,11 @@
+vXXX ######################################################################
+ XXX ######################################################################
+ ######################################################################
+
+> "c"v _v# `*95:<
+v+"I~"<\"c":< >:55+%|
+>1-:0\:"F"%v >1-:|:-1 <
+|:p/"F"\+5 <@.g1$#2$<
+>$188*2p020p10p>030p"~J"+>1-:::"F"%5+\"F"/g10g*20g+:55+/v
+ >21p > 1-:|^$< |:p/"F"\+5%"F":\p03+g03:%+55p02<
+ ^g03_^#`g1># ^#2g03$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_056_description.md b/www/statics/euler/euler_056_description.md
new file mode 100644
index 0000000..5e65e88
--- /dev/null
+++ b/www/statics/euler/euler_056_description.md
@@ -0,0 +1,3 @@
+A googol (`10^100`) is a massive number: one followed by one-hundred zeros; `100^100` is almost unimaginably large: one followed by two-hundred zeros. Despite their size, the sum of the digits in each number is only 1.
+
+Considering natural numbers of the form, ab, where `a, b < 100`, what is the maximum digital sum?
\ No newline at end of file
diff --git a/www/statics/euler/euler_056_explanation.md b/www/statics/euler/euler_056_explanation.md
new file mode 100644
index 0000000..4b5a3e0
--- /dev/null
+++ b/www/statics/euler/euler_056_explanation.md
@@ -0,0 +1,7 @@
+Here we iterate through the values of a (1..99) and do (manually) the long multiplication.
+Because we have to implement the multiplication manually we get every result from a^1 to a^99 an can easily get the digitsum for these.
+Then we remember the maximum digitsum and vòila, problem solved.
+
+A few optimizations:
+ - We ignore values where `a%10 == 0`, because these result in numbers consisting mostly of zeroes, and those will never have a high digitsum
+ - We also ignore values for a<45, because the numbers are just to short to be really significant.
\ No newline at end of file
diff --git a/www/statics/euler/euler_057.php b/www/statics/euler/euler_057.php
new file mode 100644
index 0000000..37a8c0b
--- /dev/null
+++ b/www/statics/euler/euler_057.php
@@ -0,0 +1,19 @@
+ 57,
+ 'title' => 'Square root convergents',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_057_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_057_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_057_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=057',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-057.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 87464066,
+ 'time' => 15023,
+ 'width' => 80,
+ 'height' => 54,
+ 'value' => 153,
+];
diff --git a/www/statics/euler/euler_057_code.txt b/www/statics/euler/euler_057_code.txt
new file mode 100644
index 0000000..fc4a84b
--- /dev/null
+++ b/www/statics/euler/euler_057_code.txt
@@ -0,0 +1,54 @@
+v
+
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+ ###############################################################################
+
+>77*8*2+>:0\:"O"%1+\"O"/2+p:0\:"O"%1+\"O"/8+p:0\:"O"%1+\"O"/72*+p:0\: v
+ |+1:-1p+*84/"O"\+1%"O":\0:p++*298/"O"\+1%"O":\0:p+*45/"O"\+1%"O"<
+ >$ 1"O"6p1"O"62*p1"O"56*p v
+v <
+>60*70p61*80p62*90p60*71p61*81p v > 0>$ v
+v*"o"9 p040p121p111p19*26 < ^p11_^#`g11 :-g02*5"O"<
+> 010p"O"5*>1-:::20p:"O"%1+\"O"/70g2++g\:"O"%1+\"O"/80g2++g2*10g++:55+%:#^_v
+ ^ _v#:p01/+55p++2g09/"O"\+1%"O":g02<
+ v p09%+99+6g09p08%+99+6g08p07%+99+6g07$< > 0>$ v
+ ^p12_^#`g12 :-g02*5"O"<
+ >010p"O"5*>1-:::20p:"O"%1+\"O"/71g54*++g\:"O"%1+\"O"/81g54*++g2*10g++:55+%:#^_v
+ ^ _v#:p01/+55p++*45g19/"O"\+1%"O":g02<
+ v p19%+99+6g19p18%+99+6g18p17%+99+6g17$<
+ >11g21g`!#v_40g1+40pv
+|: -1< <
+>$40g.@
\ No newline at end of file
diff --git a/www/statics/euler/euler_057_description.md b/www/statics/euler/euler_057_description.md
new file mode 100644
index 0000000..6a0b0d8
--- /dev/null
+++ b/www/statics/euler/euler_057_description.md
@@ -0,0 +1,18 @@
+It is possible to show that the square root of two can be expressed as an infinite continued fraction.
+
+~~~
+sqrt(2) = 1 + 1/(2 + 1/(2 + 1/(2 + ... ))) = 1.414213...
+~~~
+
+By expanding this for the first four iterations, we get:
+
+~~~
+1 + 1/2 = 3 /2 = 1.5
+1 + 1/(2 + 1/2) = 7 /5 = 1.4
+1 + 1/(2 + 1/(2 + 1/2)) = 17/12 = 1.41666...
+1 + 1/(2 + 1/(2 + 1/(2 + 1/2))) = 41/29 = 1.41379...
+~~~
+
+The next three expansions are `99/70`, `239/169`, and `577/408`, but the eighth expansion, `1393/985`, is the first example where the number of digits in the numerator exceeds the number of digits in the denominator.
+
+In the first one-thousand expansions, how many fractions contain a numerator with more digits than denominator?
diff --git a/www/statics/euler/euler_057_explanation.md b/www/statics/euler/euler_057_explanation.md
new file mode 100644
index 0000000..b38c93f
--- /dev/null
+++ b/www/statics/euler/euler_057_explanation.md
@@ -0,0 +1,7 @@
+I was a bit lazy with this problem. The first thing i did was search on OEIS for the numerator and denominator sequences.
+And I found both, they are **A123335** and **A000129**.
+But still there are two mayor problems:
+ - First these are recursive functions, so we need to store the last and the second last result. This is again the reason why our programs exceeds the Befunge-93 size restrictions. We need three fields for the numerator and three for the denominator (Current value | Last value | Second last value).
+ - Second the numbers become big. Like *really* big. The last values get close to four hundred digits. So - again - we need to do the calculations manually *(long multiplication and addition)*
+
+In the end we have a reasonable fast program with six 79*5 arrays for value storage.
\ No newline at end of file
diff --git a/www/statics/euler/euler_058.php b/www/statics/euler/euler_058.php
new file mode 100644
index 0000000..2252efe
--- /dev/null
+++ b/www/statics/euler/euler_058.php
@@ -0,0 +1,19 @@
+ 58,
+ 'title' => 'Spiral primes',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_058_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_058_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_058_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=058',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-058.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 78283096,
+ 'time' => 12199,
+ 'width' => 50,
+ 'height' => 17,
+ 'value' => 26241,
+];
diff --git a/www/statics/euler/euler_058_code.txt b/www/statics/euler/euler_058_code.txt
new file mode 100644
index 0000000..45d9294
--- /dev/null
+++ b/www/statics/euler/euler_058_code.txt
@@ -0,0 +1,17 @@
+v####
+v##
+v#
+v### > > > >$0v
+ > > $1v
+ >::2\`#^_:2-!#^_:2%!#^_:9\`#^_:3%!#^_:5%!#^_1 :v
+2>^:11p1-0\>:2% !#v_v v ++!!+1-g< # ^ < >v
+3 3 ^\+1\/2< \ >3-#v_$$ 1>12g\ !|>|
+p 31 vp01p03p04 g11p12< >:*11v1 >$1 #$^
+1 p+ >120pv v%g04*10g^ >\:::*11 g%1-!\^>^
+3 3g >$1\> :#v_ $ 21g >:#^_$1-!! ^
+p 03 >:!#^_\1+\2v\ ^_^#!%2/\g03p< v p33+1g33 <
+> ^1 ^p02*2g02/ <>:*40g%20g2/:20^
+ ^_^#%4g32+g31_v#`\*+55g33p32:+1g32< <
+ @.+3*2/4-2g32$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_058_description.md b/www/statics/euler/euler_058_description.md
new file mode 100644
index 0000000..31e9379
--- /dev/null
+++ b/www/statics/euler/euler_058_description.md
@@ -0,0 +1,15 @@
+Starting with 1 and spiralling anticlockwise in the following way, a square spiral with side length 7 is formed.
+
+~~~
+37 36 35 34 33 32 31
+38 17 16 15 14 13 30
+39 18 05 04 03 12 29
+40 19 06 01 02 11 28
+41 20 07 08 09 10 27
+42 21 22 23 24 25 26
+43 44 45 46 47 48 49
+~~~
+
+It is interesting to note that the odd squares lie along the bottom right diagonal, but what is more interesting is that 8 out of the 13 numbers lying along both diagonals are prime; that is, a ratio of `8/13 = 62%`.
+
+If one complete new layer is wrapped around the spiral above, a square spiral with side length 9 will be formed. If this process is continued, what is the side length of the square spiral for which the ratio of primes along both diagonals first falls below `10%`?
\ No newline at end of file
diff --git a/www/statics/euler/euler_058_explanation.md b/www/statics/euler/euler_058_explanation.md
new file mode 100644
index 0000000..90bf2c8
--- /dev/null
+++ b/www/statics/euler/euler_058_explanation.md
@@ -0,0 +1,4 @@
+It's obvious that the bottleneck of this program is the primality test.
+The numbers become here too big to create a sieve and "normal" prime testing takes too long.
+So we use the [Miller-Rabin primality test](http://en.wikipedia.org/wiki/Miller-Rabin_primality_test) that I implemented a while ago (thank [mathblog.dk](http://http://www.mathblog.dk)).
+The rest is just enumerating all the diagonals until `primes*10 59,
+ 'title' => 'XOR decryption',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_059_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_059_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_059_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=059',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-059.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 37085853,
+ 'time' => 6302,
+ 'width' => 273,
+ 'height' => 128,
+ 'value' => 107359,
+];
diff --git a/www/statics/euler/euler_059_code.txt b/www/statics/euler/euler_059_code.txt
new file mode 100644
index 0000000..606bcfe
--- /dev/null
+++ b/www/statics/euler/euler_059_code.txt
@@ -0,0 +1,30 @@
+>20g3*10gg"0"-55+*20 v
+ v"d"\+8%"d":g03+-"0"gg01+1*3g<
+ >/p30g1+30p20g1+:93+-#v_$10g1v
+|-2+!-1g02!-"u" g01p02<0p01+ <
+
+ v1p12051p > 061p > 51g61g 11p^>11g21g+!#v_11g2%21g2%+2%31^
+ |- **88 2p15:< > 31p0^ >51g"m"+61gp v
+v"+~h"< | -**882 p16:+1g16<
++ >51g1+^
+* v <
+>13p>13g:1-13p#v_ v
+v+"a"%+*298:g31< > >^ 5
+>12p892*+/:892*+%"a"+22p892*+/"a"+32pv $ $ 5
+v p430 < $ $ 6
+>014p 55*6*8* >:3%1+24p::"d"%8+\"d"/g"m"+24g2gg :" "\`#^_:"~"`| 8
+ ^-1 _v#-" "_v#-9p41+1:g41< *
+ >$$ ^ *
+v < >$ ^ *
+ > $ ^ 1
+>:3%1+24p::"d"%8+\"d"/g"m"+24g2gg :" "\`#^_:"~"`| 5
+^-1_v#: _v#-"e"< p
+ ^ : p43+1g43< 0
+ >$34g23g`#v_ ^ 2
+ >34g23p 32g22g12g 43p53p63p ^ 5
+ p
+v <
+v p51-1<
+>15g:"d"%8+\"d"/g"m"+15g3%4+3gg:25g+25p15g:"d"%8+\"d"/p15g:|
+ >$25g.@
diff --git a/www/statics/euler/euler_059_description.md b/www/statics/euler/euler_059_description.md
new file mode 100644
index 0000000..4b607c6
--- /dev/null
+++ b/www/statics/euler/euler_059_description.md
@@ -0,0 +1,9 @@
+Each character on a computer is assigned a unique code and the preferred standard is ASCII (American Standard Code for Information Interchange). For example, uppercase `A = 65,` `asterisk (*) = 42`, and `lowercase k = 107`.
+
+A modern encryption method is to take a text file, convert the bytes to ASCII, then XOR each byte with a given value, taken from a secret key. The advantage with the XOR function is that using the same encryption key on the cipher text, restores the plain text; for example, `65 XOR 42 = 107`, then `107 XOR 42 = 65`.
+
+For unbreakable encryption, the key is the same length as the plain text message, and the key is made up of random bytes. The user would keep the encrypted message and the encryption key in different locations, and without both "halves", it is impossible to decrypt the message.
+
+Unfortunately, this method is impractical for most users, so the modified method is to use a password as a key. If the password is shorter than the message, which is likely, the key is repeated cyclically throughout the message. The balance for this method is using a sufficiently long password key for security, but short enough to be memorable.
+
+Your task has been made easy, as the encryption key consists of three lower case characters. Using [cipher.txt](https://projecteuler.net/project/resources/p059_cipher.txt) *(right click and 'Save Link/Target As...')*, a file containing the encrypted ASCII codes, and the knowledge that the plain text must contain common English words, decrypt the message and find the sum of the ASCII values in the original text.
\ No newline at end of file
diff --git a/www/statics/euler/euler_059_explanation.md b/www/statics/euler/euler_059_explanation.md
new file mode 100644
index 0000000..e4be059
--- /dev/null
+++ b/www/statics/euler/euler_059_explanation.md
@@ -0,0 +1,12 @@
+This task had a lot of Befunge specific problems, but first let's look at the solving strategy:
+ - We go through all `26^3` passwords and test look if they generate illegal characters (smaller 32 or bigger 127).
+ - We also see if one of the first twelve characters is a space, assuming the first word is no longer than twelve characters.
+ - The leaves us with around one-hundred viable passwords.
+ - We use the fact that in the English language the letter `e` is pretty common and take the password with the highest count of `e`.
+ - The rest is just decrypting the text and counting the values.
+
+Now to our Befunge specific problems:
+ - First we need to input the raw data. Our best call is inserting the data directly into the program and then parsing it in the first step into an array.
+ - The next problem is the missing xor operator. To perform an xor operation we need to go through all bits and xor them individually (`a xor b == (a+b) % 2`). This is an extremely pricey operation. And to speed this up we generate an complete 128x128 xor look up-table with all possible xor operations.
+
+All in all a not really optimal problem for Befunge but still a fun challenge
\ No newline at end of file
diff --git a/www/statics/euler/euler_060.php b/www/statics/euler/euler_060.php
new file mode 100644
index 0000000..de7b057
--- /dev/null
+++ b/www/statics/euler/euler_060.php
@@ -0,0 +1,19 @@
+ 60,
+ 'title' => 'Prime pair sets',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_060_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_060_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_060_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=060',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-060.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 8609996835,
+ 'time' => 2032350,
+ 'width' => 3323,
+ 'height' => 3360,
+ 'value' => 26033,
+];
diff --git a/www/statics/euler/euler_060_code.txt b/www/statics/euler/euler_060_code.txt
new file mode 100644
index 0000000..6f3e403
--- /dev/null
+++ b/www/statics/euler/euler_060_code.txt
@@ -0,0 +1,66 @@
+vXXXX /#...## ####
+ XXX # # ####
+ XXXXXX. . ####
+ XX . . ####
+ XXX . . ####
+ XXXXX # # ####
+ XXX ##...## ####
+
+>55+12p "d!"*22p 26522g+++62p 22g:*52p 12g22g*42p 523p v
+ v p232< >032p v
+v p0+1g26p0g26:" "< _^#`g23g24<
+>"X"32g:12g%62g+\12g/p32g>32g+:42g\` #v_$>32g1+:32p:12g%62g+\12g/g" "-|
+ ^p/g21\+g26%g21:\" ":< ^ <
+v <
+ >52g >1-:0\:22g%9+\22g/1+pv
+ |: <
+ v $<
+>22g1+ >1- :0\8\p v
+ |: <
+v $<
+ >22g >1-:0\9+0p v
+ |: <
+ v $<
+>0 113p > ::12g%62g+\12g/g"X"-#v_:13g8+0p:713gp22g13g1+:13p\`#v_v
+ |-g24:+1 < <
+v $< <
+>114p 024p "@@@@` "+****34p 015p 025p 035p 045p 055p 065p v
+v < <
+>14g#v_34g.@
+ >14g1+5g1+:14g1+5p22g-#v_14g1-14p24g714g1+5g1+g-24p^
+ vg41g32g+1g5+1g417g42g43<
+ >-*+`#v_14g1-14p24g714g1+5g1+g-24p ^
+ v-1g41<
+ :>:1+5g1+14g1+5g9+\g#v_$ ^
+ >|:-1 <
+ $
+ >14g1+5gv > > > >$0v
+ v < >55+*\:v > > $1v
+ >:1+8\g#v_:::1\1+8\p36p9+0g26p1+v>:9+0g:26 g>\:#v_$+:2\`#^_:2-!#^_:2%!#^_:9\`#^_:3%!#^_:5%!#^_1 :v
+ v2:< ^\/+55< v\ p13:+1g13:_v#-3 2g-|< >:11p1-0\>:2% !#v_v v ++!!+1-g< # ^ < >v
+ v < $<- ^\+1\/2< \ >3-#v_$$ 1>31g\ !|> |
+ g vp01p03p04 g11p12< >:*11v1 >$1 #$^ :
+ 2 >120pv v%g04*10g^ >\:::*11 g%1-!\^>^
+ : >$1\> :#v_ $ 21g >:#^_$1-!! ^
+ + >:!#^_\1+\2v\ ^_^#!%2/\g03p<
+ 1 ^p02*2g02/ <>:*40g%20g2/:20^
+ v g62\g62g0+9: <
+ ^ p+1g63+9\<<
+ > > > >$0v
+ >55+*\:v > > $1v
+ > \>\:#v_$+:2\`#^_:2-!#^_:2%!#^_:9\`#^_:3%!#^_:5%!#^_1 :v
+ ^\/+55< v\ p13:+1g13:_v#-3 :11p1-0\>:2% !#v_v v ++!!+1-g< # ^ < >:1^
+ ^\+1\/2< \ >3-#v_$$ 1>31g\ !|>|
+ vp01p03p04 g11p12< >:*11v1 >$1 #$^>:0^
+ >120pv v%g04*10g^ >\:::*11 g%1-!\^>^
+ >$1\> :#v_ $ 21g >:#^_$1-!! ^
+ >:!#^_\1+\2v\ ^_^#!%2/\g03p<
+ ^p02*2g02/ <>:*40g%20g2/:20^
+ >24g714g1+5g1+g+24p14g1+14p14g5g14g1+5p v
+ >14g23g-| >24g714g1+5g1+g+34p v
+ >34g24g714g1+5g1+g+`#^_ >14g1-14p24g7 v
+^ 61,
+ 'title' => 'Cyclical figurate numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_061_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_061_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_061_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=061',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-061.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 50105245,
+ 'time' => 14414,
+ 'width' => 80,
+ 'height' => 25,
+ 'value' => 28684,
+];
diff --git a/www/statics/euler/euler_061_code.txt b/www/statics/euler/euler_061_code.txt
new file mode 100644
index 0000000..afcffb2
--- /dev/null
+++ b/www/statics/euler/euler_061_code.txt
@@ -0,0 +1,25 @@
+v$$ ### ---------------------------------------------------------------- ###
+ $$ ### ---------------------------------------------------------------- ###
+ $ ### ---------------------------------------------------------------- ###
+ $ ### ---------------------------------------------------------------- ###
+ $ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ ### ---------------------------------------------------------------- ###
+ v_v#! _v# <1 g02$$<
+ ##### 1 v p02g01_v#! # g02$_v#!:p\+9%*88g02 <0
+> # 6 # 10p 288** 20p>20g1-20p10g>1-:0\2*20g88*/+^^ $<0p03+1g03 p+*2g02/*88g<
+ ##### 0 >20g1-20p030p0>1+::::*\-2/20g1+*+:"}"8*\`#^_:"ec"*`#^_30g88*%9+30^
+ >g>1-:0\5\p:0\6\p:0\7\p:#v_$ 01-60p011p v
+v< $_^#!: <0 < < <$$<
+>611gg1+611gp611gg12p511gg13p12g10g-!#v_13g"_ "+`#v_712gg#^_13g88* %9+13g88*/12v
+^/611g1-g2*+g"d"%14g"d"/-*#^_10g1-11g`!|
+^2*+g:.+55+,21g1+:21p10g-#v_" = ",,,,.@ >88*/60g2*+g"d"/-#^_v
+^gg126/*88gg125+9%*88gg125<0p120 <
\ No newline at end of file
diff --git a/www/statics/euler/euler_061_description.md b/www/statics/euler/euler_061_description.md
new file mode 100644
index 0000000..3ef7bcb
--- /dev/null
+++ b/www/statics/euler/euler_061_description.md
@@ -0,0 +1,21 @@
+Triangle, square, pentagonal, hexagonal, heptagonal, and octagonal numbers
+are all figurate (polygonal) numbers and are generated by the following formulae:
+
+~~~
+Triangle P3,n=n(n+1)/2 1, 3, 6, 10, 15, ...
+Square P4,n=n2 1, 4, 9, 16, 25, ...
+Pentagonal P5,n=n(3n?1)/2 1, 5, 12, 22, 35, ...
+Hexagonal P6,n=n(2n?1) 1, 6, 15, 28, 45, ...
+Heptagonal P7,n=n(5n?3)/2 1, 7, 18, 34, 55, ...
+Octagonal P8,n=n(3n?2) 1, 8, 21, 40, 65, ...
+~~~
+
+The ordered set of three 4-digit numbers: `8128, 2882, 8281`, has three interesting properties.
+
+ - The set is cyclic, in that the last two digits of each number is the first two digits of the next number (including the last number with the first).
+ - Each polygonal type: triangle (`P(3,127)=8128`), square (`P(4,91)=8281`), and pentagonal (`P(5,44)=2882`), is represented by a different number in the set.
+ - This is the only set of 4-digit numbers with this property.
+
+Find the sum of the only ordered set of six cyclic 4-digit numbers for which each polygonal type:
+triangle, square, pentagonal, hexagonal, heptagonal, and octagonal,
+is represented by a different number in the set.
\ No newline at end of file
diff --git a/www/statics/euler/euler_061_explanation.md b/www/statics/euler/euler_061_explanation.md
new file mode 100644
index 0000000..a1d4dc2
--- /dev/null
+++ b/www/statics/euler/euler_061_explanation.md
@@ -0,0 +1,12 @@
+Pretty cool problem, I have to say.
+
+It's one of these problem that you can easily make dynamic. In the middle-left of this program you see the number `6` surrounded with `#`.
+This is the "amount of resulting numbers" parameter of our program. For this Euler-problem you need to set this to `6`.
+But for debugging purposes I mostly tested it with `3`. And if you want you can try it out with bigger numbers `7` or `8`.
+*(But then you need to move the code down a bit - otherwise the cache-part will intersect with the code-part)*.
+
+With this number we first generate all the [polygon-numbers](https://en.wikipedia.org/wiki/Polygonal_number) from `3` to `SIDES_COUNT + 2` with the formula `(n-2) * (n^2 - n)/2 + n`.
+Then we go recursively through all these numbers. First we test triangle[1] with square[1], then with square[2] and so on. *(The recursion is - as always - just a stack and a stack pointer)*.
+
+A last note: This was *(until now)* probably the hardest program to fit in the befunge 80x25 size restriction.
+I *barely* managed to get it (and now its exactly 80x25) and I had to use quite some trickery.
\ No newline at end of file
diff --git a/www/statics/euler/euler_062.php b/www/statics/euler/euler_062.php
new file mode 100644
index 0000000..32b848d
--- /dev/null
+++ b/www/statics/euler/euler_062.php
@@ -0,0 +1,19 @@
+ 62,
+ 'title' => 'Cubic permutations',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_062_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_062_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_062_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=062',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-062.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 952323293,
+ 'time' => 363264,
+ 'width' => 505,
+ 'height' => 58,
+ 'value' => 127035954683,
+];
diff --git a/www/statics/euler/euler_062_code.txt b/www/statics/euler/euler_062_code.txt
new file mode 100644
index 0000000..65fd304
--- /dev/null
+++ b/www/statics/euler/euler_062_code.txt
@@ -0,0 +1,18 @@
+v $ # ... #
+ $ # #
+ $ . .
+ . .
+ $ . .
+ $ . .
+ # #
+ # ... #
+ v _v#!:p/g42\+ <
+>3 28p "K": 24p 88+: 25p*:26p >1-:0\:24g%4^
+v < v+1 <
+0 |-g02<
+>1+:::**:22p 0\v v\-1 <>20p0>:3*:24g%4+\24 g/g:|
+$ v+55:<>\1>9*\:|: @$$.g/g42\+4%g42:+1$ <
+ >%\:#^|#/+55\$<+ > 3*:2+:24g%4+\24g/g1+:28g-!|
+ >$ #\>#<>\# :#+_^ >*::2v vp/g42\+4%g42:+2\<
+^p/g42\+4%g42:+2\1p/g42\+4%g42:+1\g22p/g42\+4%g42:\g0 <
+^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_062_description.md b/www/statics/euler/euler_062_description.md
new file mode 100644
index 0000000..234f732
--- /dev/null
+++ b/www/statics/euler/euler_062_description.md
@@ -0,0 +1,4 @@
+The cube, `41063625 (345^3)`, can be permuted to produce two other cubes: `56623104 (384^3)` and `66430125 (405^3)`.
+In fact, `41063625` is the smallest cube which has exactly three permutations of its digits which are also cube.
+
+Find the smallest cube for which exactly five permutations of its digits are cube.
\ No newline at end of file
diff --git a/www/statics/euler/euler_062_explanation.md b/www/statics/euler/euler_062_explanation.md
new file mode 100644
index 0000000..06b7c8c
--- /dev/null
+++ b/www/statics/euler/euler_062_explanation.md
@@ -0,0 +1,7 @@
+Only after at least sixty-two mathematical programs in befunge you will **truly** appreciate a hashtable.
+
+For real, everything would be so much better if I could retrieve this stuff in `O(1)`.
+
+My approach is pretty straight-forward. We calculate an permutation-insensitive hash.
+Then store them together with the times it appeared in a hashmap *(I mean a list -.-)*.
+Now we just go through all the cubes until a single hash appeared five times. In C# with a Dictionary this takes around 10ms.
\ No newline at end of file
diff --git a/www/statics/euler/euler_063.php b/www/statics/euler/euler_063.php
new file mode 100644
index 0000000..82e170e
--- /dev/null
+++ b/www/statics/euler/euler_063.php
@@ -0,0 +1,19 @@
+ 63,
+ 'title' => 'Powerful digit counts',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_063_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_063_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_063_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=063',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-063.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 8880369,
+ 'time' => 2762,
+ 'width' => 80,
+ 'height' => 10,
+ 'value' => 49,
+];
diff --git a/www/statics/euler/euler_063_code.txt b/www/statics/euler/euler_063_code.txt
new file mode 100644
index 0000000..ba89b7c
--- /dev/null
+++ b/www/statics/euler/euler_063_code.txt
@@ -0,0 +1,10 @@
+v XXXX #######################################################################
+ XX
+ v1\1p12::+1 \+g2<
+0 v9p03p02< \g12:+1<^2\p22_v
+1 >v v < v-\"P"< :$
+> :v1v>0p>9>:"0"\0p1+:"O"-|>:0g"0"-||!`g12<-$
+ :p\3v p050p04"O"#1 $#< :21g-|\.
+ 211p> 40g0g"0"-2 0g*50g+:55+%"0"v>$55+0v+@
+ >^20|-8p04:-1g04 p05/+5 #5p0g04+<>5#$5#<^
+ >^>30g1-:30p #^_9 ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_063_description.md b/www/statics/euler/euler_063_description.md
new file mode 100644
index 0000000..a7af47b
--- /dev/null
+++ b/www/statics/euler/euler_063_description.md
@@ -0,0 +1,4 @@
+The 5-digit number, `16807=7^5`, is also a fifth power.
+Similarly, the 9-digit number, `134217728=8^9`, is a ninth power.
+
+How many n-digit positive integers exist which are also an nth power?
\ No newline at end of file
diff --git a/www/statics/euler/euler_063_explanation.md b/www/statics/euler/euler_063_explanation.md
new file mode 100644
index 0000000..fab9ae5
--- /dev/null
+++ b/www/statics/euler/euler_063_explanation.md
@@ -0,0 +1,6 @@
+After all the previous programs, this one is surprisingly ... dense (the main code-block is 54x8).
+
+The algorithm is quickly explained for each length n we calculate the numbers `1^n`, `2^n` ... until `9^n` and see which have a length of `n`.
+(From `10^n` upwards the condition is impossible, because `10^n` has `(n+1)` digits).
+
+The main problem is that the numbers exceed Int64. So we need to implement long multiplication ... again. (see problem 16, 20, 29, 56 and 57)
\ No newline at end of file
diff --git a/www/statics/euler/euler_064.php b/www/statics/euler/euler_064.php
new file mode 100644
index 0000000..ba062b9
--- /dev/null
+++ b/www/statics/euler/euler_064.php
@@ -0,0 +1,19 @@
+ 64,
+ 'title' => 'Odd period square roots',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_064_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_064_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_064_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=064',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-064.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 24936143,
+ 'time' => 5804,
+ 'width' => 51,
+ 'height' => 9,
+ 'value' => 1322,
+];
diff --git a/www/statics/euler/euler_064_code.txt b/www/statics/euler/euler_064_code.txt
new file mode 100644
index 0000000..17e1ca4
--- /dev/null
+++ b/www/statics/euler/euler_064_code.txt
@@ -0,0 +1,9 @@
+v###
+ #####
+0
+">>1-:0\951p11p021p131v v12g14 p150 p13/g<
+I vp01g03_v#-g01:_v#- <>g+31g/ :31g*21g-21v1
+i @ >:30p:20 g\/+2/: 30g^^12p14:<>11g21g:*-3 ^
+ * . > #$ >$30g::*11g-||+g15-1g13p<
+"+ $ ^p02:p010g11p1< v\+1\<>>0>\#+ #1:#$_v
+>^^_^#-2: < _^# %2$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_064_description.md b/www/statics/euler/euler_064_description.md
new file mode 100644
index 0000000..bdffd67
--- /dev/null
+++ b/www/statics/euler/euler_064_description.md
@@ -0,0 +1,53 @@
+All square roots are periodic when written as continued fractions and can be written in the form:
+
+~~~
+sqrt(N) = a0 + 1 / (a1 + 1 / (a2 + 1 / (a3 + ... )))
+~~~
+
+For example, let us consider `sqrt(23)`:
+
+~~~
+sqrt(23)
+ = 4 + sqrt(23) - 4
+ = 4 + 1 / ( 1 / ( sqrt(23) - 4 ) )
+ = 4 + 1 / ( 1 + ( sqrt(23) - 3 ) / 7)
+~~~
+
+If we continue we would get the following expansion:
+~~~
+sqrt(23) = 4 + 1/(1 + 1/(3 + 1/(1 + 1/(8 + ... ))))
+~~~
+
+The process can be summarised as follows:
+
+a | Step 1 | Step 1 |Step 1
+-----|------------------------|-------------------------|----------------------
+`a0` | `4`, `1/(sqrt(23) - 4` | `1*(sqrt(23) + 4) / 7` | `1 + (sqrt(23) - 3)/7`
+`a1` | `1`, `7/(sqrt(23) - 3` | `7*(sqrt(23) + 3) / 14` | `3 + (sqrt(23) - 3)/2`
+`a2` | `3`, `2/(sqrt(23) - 3` | `2*(sqrt(23) + 3) / 14` | `1 + (sqrt(23) - 4)/7`
+`a3` | `1`, `7/(sqrt(23) - 4` | `7*(sqrt(23) + 4) / 7` | `8 + (sqrt(23) - 4)/1`
+`a4` | `8`, `1/(sqrt(23) - 4` | `1*(sqrt(23) + 4) / 7` | `1 + (sqrt(23) - 3)/7`
+`a5` | `1`, `7/(sqrt(23) - 3` | `7*(sqrt(23) + 3) / 14` | `3 + (sqrt(23) - 3)/2`
+`a6` | `3`, `2/(sqrt(23) - 3` | `2*(sqrt(23) + 3) / 14` | `1 + (sqrt(23) - 4)/7`
+`a7` | `1`, `7/(sqrt(23) - 4` | `7*(sqrt(23) + 4) / 7` | `8 + (sqrt(23) - 4)/1`
+
+It can be seen that the sequence is repeating. For conciseness, we use the notation `sqrt(23) = [4;(1,3,1,8)]`, to indicate that the block `(1,3,1,8)` repeats indefinitely.
+
+The first ten continued fraction representations of (irrational) square roots are:
+
+~~~
+sqrt( 2) = [1;(2)], period=1
+sqrt( 3) = [1;(1,2)], period=2
+sqrt( 5) = [2;(4)], period=1
+sqrt( 6) = [2;(2,4)], period=2
+sqrt( 7) = [2;(1,1,1,4)], period=4
+sqrt( 8) = [2;(1,4)], period=2
+sqrt(10) = [3;(6)], period=1
+sqrt(11) = [3;(3,6)], period=2
+sqrt(12) = [3;(2,6)], period=2
+sqrt(13) = [3;(1,1,1,1,6)], period=5
+~~~
+
+Exactly four continued fractions, for `N <= 13`, have an odd period.
+
+How many continued fractions for `N <= 10000` have an odd period?
\ No newline at end of file
diff --git a/www/statics/euler/euler_064_explanation.md b/www/statics/euler/euler_064_explanation.md
new file mode 100644
index 0000000..883f128
--- /dev/null
+++ b/www/statics/euler/euler_064_explanation.md
@@ -0,0 +1,9 @@
+For this I had to re-use my old [integer-squareroot](https://en.wikipedia.org/wiki/Integer_square_root) implementation
+and I ported an [algorithm](http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/cfINTRO.html#section7) for calculating the continued fraction to befunge.
+
+The rest is just iterating through all the values and trying to optimize for speed.
+
+Here two useful snippets I made while solving this puzzle:
+
+ - Calculating the **sum** of an zero-terminated array on the stack: `>\# :#+_+`
+ - Calculating the **count** of an zero-terminated array on the stack: `0>\#+ #1:#$_$`
\ No newline at end of file
diff --git a/www/statics/euler/euler_065.php b/www/statics/euler/euler_065.php
new file mode 100644
index 0000000..6e6c10b
--- /dev/null
+++ b/www/statics/euler/euler_065.php
@@ -0,0 +1,19 @@
+ 65,
+ 'title' => 'Convergents of e',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_065_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_065_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_065_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=065',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-065.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 477489,
+ 'time' => 124,
+ 'width' => 80,
+ 'height' => 14,
+ 'value' => 272,
+];
diff --git a/www/statics/euler/euler_065_code.txt b/www/statics/euler/euler_065_code.txt
new file mode 100644
index 0000000..17c46d4
--- /dev/null
+++ b/www/statics/euler/euler_065_code.txt
@@ -0,0 +1,14 @@
+v $$$ #######################################################################
+
+ #######################################################################
+
+ v -1<
+>"F">:9+"0"\0p:9+"0"\2p:|
+v"c"p040p2"O1"p0"O0" $<
+ >$1 v@.:1-3%:!| >:1+3/2*v +>g*+40g+:55+%"0"+30g2p55+/40p:9-|
+>:| >2-#^_1 >20 p "O"v # $
+| ># #+ #1 #: #- #12# ^# ># ^# <
+$ >\v >\:!|
+>0"F">:9+2g"0"-:| >:!|1 +<
+ ^ -1_ ^#1<
\ No newline at end of file
diff --git a/www/statics/euler/euler_065_description.md b/www/statics/euler/euler_065_description.md
new file mode 100644
index 0000000..5160a22
--- /dev/null
+++ b/www/statics/euler/euler_065_description.md
@@ -0,0 +1,32 @@
+The infinite continued fraction can be written, `sqrt(2) = [1;(2)]`, `(2)` indicates that `2` repeats ad infinitum.
+In a similar way, `sqrt(23) = [4;(1,3,1,8)]`.
+
+It turns out that the sequence of partial values of continued fractions for square roots provide the best rational approximations.
+Let us consider the convergents for `sqrt(2)`.
+
+~~~
+1 + 1/2 = 3/2
+1 + 1/(2+ 1/2) = 7/5
+1 + 1/(2+ 1/(2+ 1/2)) = 17/12
+1 + 1/(2+ 1/(2+ 1/(2+ 1/2))) = 41/29
+~~~
+
+Hence the sequence of the first ten convergents for `sqrt(2)` are:
+~~~
+1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, ...
+~~~
+
+What is most surprising is that the important mathematical constant,
+
+~~~
+e = [2; 1,2,1, 1,4,1, 1,6,1 , ... , 1,2k,1, ...]
+~~~
+
+The first ten terms in the sequence of convergents for `e` are:
+~~~
+2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, ...
+~~~
+
+The sum of digits in the numerator of the 10th convergent is `1+4+5+7=17`.
+
+Find the sum of digits in the numerator of the 100th convergent of the continued fraction for `e`.
\ No newline at end of file
diff --git a/www/statics/euler/euler_065_explanation.md b/www/statics/euler/euler_065_explanation.md
new file mode 100644
index 0000000..dfbab7b
--- /dev/null
+++ b/www/statics/euler/euler_065_explanation.md
@@ -0,0 +1,21 @@
+Nice algorithm if you see the pattern in the numerators and denominators.
+
+~~~
+denom(n+1) = denom(n) + numer(n) * frac(n)
+numer(n+1) = denom(n)
+~~~
+
+and the fraction at position n is calculated by ([OEIS-A003417](https://oeis.org/A003417)):
+
+~~~
+int GetFrac(int idx)
+{
+ if (idx == 0) return 2;
+ if ((idx-1) % 3 == 0) return 1;
+ if ((idx-1) % 3 == 1) return ((idx+1)/3)*2;
+ if ((idx-1) % 3 == 2) return 1;
+ return 2;
+}
+~~~
+
+The rest is just multiplication and long addition (we exceed the 64bit range) a hundred times ...
\ No newline at end of file
diff --git a/www/statics/euler/euler_066.php b/www/statics/euler/euler_066.php
new file mode 100644
index 0000000..5fc5589
--- /dev/null
+++ b/www/statics/euler/euler_066.php
@@ -0,0 +1,19 @@
+ 66,
+ 'title' => 'Diophantine equation',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_066_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_066_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_066_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=066',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-066.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 262481767,
+ 'time' => 55831,
+ 'width' => 80,
+ 'height' => 25,
+ 'value' => 661,
+];
diff --git a/www/statics/euler/euler_066_code.txt b/www/statics/euler/euler_066_code.txt
new file mode 100644
index 0000000..383f18d
--- /dev/null
+++ b/www/statics/euler/euler_066_code.txt
@@ -0,0 +1,25 @@
+vYYY ################
+ XBXX ################
+ ZZZ ################
+ N
+ OOO ################
+ ################
+ ################
+ ################ v 9::p4+9\g5+9::p1+9\g2+9: <
+ ################ >+6g\9+5p:1-\!v0 <
+ ################ v $_::9+1g\9+0p:^
+ v _v#-*"}"8p13:+1g13$< # <
+>"@ ":*:**21p331p013p88 +>:8+0\8v >11g.@ >+8p:1-\!| >-22g/22p35*^
+v p02:p010g13<$<_^#!:-1p< ^9\g2+9::<# ^*:g21g13p21-g21*g 22<
+vp01g03_v#-g01:_v#- <^ :30p:20 g\/+2/: 30g^ >88 +>:8+0\5p:8+0\4p:8+^ > `^ >$$ $v2
+ > >$30g:41p:*31g-| >$164*1p164*4p012p122pv 0 >$1+:9-8- !| 03
+^p02:p010g13p13+1g13 # 3# 5# *# # ^
+>:::9+0g\9+1g32g*+13g+:v v 53< |!\-1:g42$< >::9+7g\9+9g- |
+|\-1:p2+9\%g12 p31/g12 < # >$ 014p35 *>:9+0\ v|!-9g43-1p7g43%g12p41/g12 :+g<
+>$35*:::9+4g\9+5g32g*+13g+v $ >*>2 4p35* >::24g+# 6-34p9+2g24g9+2gv>1v7
+>:::9+4g\9+5g32g*+13g+v <|!\-1:g42$< |\-1:p7< ^ # < -g
+|\-1:p6+9\%g12p31/g12:<> # :9+0\v| !-9 g43-1p9g43%g12p41/g12:+g9g43$114p35* ^ >*>2 4p35*#9> ::2 4g+6-34p9+6g24g9+6g31g**14g+^> 4g +3^
+ ^ _^#\-1:p< ^53$< ^ $<
\ No newline at end of file
diff --git a/www/statics/euler/euler_066_description.md b/www/statics/euler/euler_066_description.md
new file mode 100644
index 0000000..bb990f5
--- /dev/null
+++ b/www/statics/euler/euler_066_description.md
@@ -0,0 +1,23 @@
+Consider quadratic Diophantine equations of the form:
+
+~~~
+x^2 – Dy^2 = 1
+~~~
+
+For example, when `D=13`, the minimal solution in `x` is `649^2 – 13×180^2 = 1`.
+
+It can be assumed that there are no solutions in positive integers when D is square.
+
+By finding minimal solutions in `x` for `D = {2, 3, 5, 6, 7}`, we obtain the following:
+
+~~~
+3^2 – 2×2^2 = 1
+2^2 – 3×1^2 = 1
+9^2 – 5×4^2 = 1
+5^2 – 6×2^2 = 1
+8^2 – 7×3^2 = 1
+~~~
+
+Hence, by considering minimal solutions in `x` for `D <= 7`, the largest `x` is obtained when `D=5`.
+
+Find the value of `D <= 1000` in minimal solutions of `x` for which the largest value of `x` is obtained.
\ No newline at end of file
diff --git a/www/statics/euler/euler_066_explanation.md b/www/statics/euler/euler_066_explanation.md
new file mode 100644
index 0000000..085d22c
--- /dev/null
+++ b/www/statics/euler/euler_066_explanation.md
@@ -0,0 +1,30 @@
+Okay I admit this one took me five days to complete (with two days pause in between, because of I kinda got frustrated).
+
+I needed eight numbers that were too big for int64 so I encoded them in base-67108864 (`2^26`).
+The reason for this specific number (and I had to fail first to see the problem with bigger bases) is that the biggest calculation I do is `D_0 * D_0 * D * 1`.
+Which is maximally `2^26 * 2^26 * 2^10` which fits *barely* in an signed 64-bit integer.
+
+Also I needed to first write code to multiply two numbers, both in base-67108864 and both bigger than `2^63`. Let me tell you that was no fun and long-addition is far easier to implement than long-multiplication.
+Especially after first I did everything wrong and then had to redo it :/
+
+The first running version of this program was full of debug statements (even more than normally) and had a size of 200x60. (You can look at it, it's the `Problem-066 (annotated)` file).
+But after that I managed to shrink it quite a bit :D I even *(barely)* managed to fit it in the 80x25 restriction.
+I have the feeling I've gotten pretty good at compacting my programs...
+
+But back to the interesting stuff, how did I solve this one:
+
+I can' really explain everything in detail here, so I give you a few useful links:
+
+ - [https://en.wikipedia.org/wiki/Diophantine_equation](https://en.wikipedia.org/wiki/Diophantine_equation)
+ - [https://en.wikipedia.org/wiki/Pell's_equation](https://en.wikipedia.org/wiki/Pell%27s_equation)
+ - [https://en.wikipedia.org/wiki/Generalized_continued_fraction](https://en.wikipedia.org/wiki/Generalized_continued_fraction)
+ - [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/cfINTRO.html#section9.4](http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/cfINTRO.html#section9.4)
+
+If you want to have the `(x|y)` solution for a number D:
+
+ - First you calculate the continuous fraction of `sqrt(D)`
+ - For the continuous fraction you calculate the convergents `hi / ki` (read the link about Pell's equation)
+ - Now you just test if `hi` and `ki` are solutions, if not go on to the next convergent pair
+
+In the end the algorithm is really not that complex (around 30 lines in C#) but all the numbers get so big - and you need to multiply and add the already big numbers together so you get even bigger immediate values.
+So on a last note I could say ... I wished the numbers in befunge were unlimited.
\ No newline at end of file
diff --git a/www/statics/euler/euler_067.php b/www/statics/euler/euler_067.php
new file mode 100644
index 0000000..aa85582
--- /dev/null
+++ b/www/statics/euler/euler_067.php
@@ -0,0 +1,19 @@
+ 67,
+ 'title' => 'Maximum path sum II',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_067_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_067_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_067_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=067',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-067.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 650537,
+ 'time' => 266,
+ 'width' => 299,
+ 'height' => 101,
+ 'value' => 7273,
+];
diff --git a/www/statics/euler/euler_067_code.txt b/www/statics/euler/euler_067_code.txt
new file mode 100644
index 0000000..26cf2fd
--- /dev/null
+++ b/www/statics/euler/euler_067_code.txt
@@ -0,0 +1,12 @@
+$$>"d" 00p00g1-20p010p>10g3*:20g1+g"0"-55+*\1+20g1+g"0"-+10g20g1+p10g1+:10p20g-1-#v_20g:1-20p010p#v_v
+59 ^ < < v
+73 41 v <
+52 40 09 > $v
+26 53 06 34 >00g2-:10p 20p > 10g20g1+g 10g20g2+g : 10g1+20g2+g -:0`>#^_-> + 10g20g1+ p 10g:1-10p#v_20g:1-:20p10p#v_ 01g.@
+10 51 87 86 81 ^ < <
+61 95 66 57 25 68
+90 81 80 38 92 67 73
+30 28 51 76 81 18 75 44
+84 14 95 87 62 81 17 78 58
+
+... ... ...
\ No newline at end of file
diff --git a/www/statics/euler/euler_067_description.md b/www/statics/euler/euler_067_description.md
new file mode 100644
index 0000000..6310fde
--- /dev/null
+++ b/www/statics/euler/euler_067_description.md
@@ -0,0 +1,14 @@
+By starting at the top of the triangle below and moving to adjacent numbers on the row below, the maximum total from top to bottom is 23.
+
+~~~
+3
+7 4
+2 4 6
+8 5 9 3
+~~~
+
+That is, 3 + 7 + 4 + 9 = 23.
+
+Find the maximum total from top to bottom in [triangle.txt](https://projecteuler.net/project/resources/p067_triangle.txt) (right click and 'Save Link/Target As...'), a 15K text file containing a triangle with one-hundred rows.
+
+*NOTE: This is a much more difficult version of [Problem 18]. It is not possible to try every route to solve this problem, as there are 299 altogether! If you could check one trillion (1012) routes every second it would take over twenty billion years to check them all. There is an efficient algorithm to solve it. ;o)*
\ No newline at end of file
diff --git a/www/statics/euler/euler_067_explanation.md b/www/statics/euler/euler_067_explanation.md
new file mode 100644
index 0000000..e4b1225
--- /dev/null
+++ b/www/statics/euler/euler_067_explanation.md
@@ -0,0 +1 @@
+see [Problem-018]
\ No newline at end of file
diff --git a/www/statics/euler/euler_068.php b/www/statics/euler/euler_068.php
new file mode 100644
index 0000000..6533e62
--- /dev/null
+++ b/www/statics/euler/euler_068.php
@@ -0,0 +1,19 @@
+ 68,
+ 'title' => 'Magic 5-gon ring',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_068_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_068_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_068_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=068',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-068.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 304112,
+ 'time' => 78,
+ 'width' => 39,
+ 'height' => 25,
+ 'value' => 6531031914842725,
+];
diff --git a/www/statics/euler/euler_068_code.txt b/www/statics/euler/euler_068_code.txt
new file mode 100644
index 0000000..676db6a
--- /dev/null
+++ b/www/statics/euler/euler_068_code.txt
@@ -0,0 +1,25 @@
+v X X ##########
+ X OOOOOOOOOO
+>":"v v < <
+v < vp1+9-"0"g0+9p03:-1g03"O" <
+>90p030p>30g9+0g1-:30g9+0p"0"-:70p0\`|
+v g03_^#! -"O"g1+9g07 #<$
+>:#v_70g5` >|
+v-1< v _v#!`g039$ <
+>:#v_ 70g9-! ^
+v-1< >"X"70g9+1p":"30g1+:30p9+0p^
+>:#v_ 90+0g91+0g92+0g++51p70g9-! ^
+v-1< >91+0g"/"- 98+0g"/"- 99+0g"/"- v
+>:#v_90g"0"-70g` ^
+v-1< v-"/"g0+79 -"/"g0+69 -"/"g0+89 <
+>:#v_ 92+0g93+0g94+0g++51g-!!70g9-!+ ^
+v-1< >96+0g"/"- 94+0g"/"- 95+0g"/"- v
+>:#v_90g"0"-70g` ^
+v-1< v-"/"g0+39 -"/"g0+29 -"/"g0+49 <
+>:#v_ 94+0g95+0g96+0g++51g-!!70g9-!+ ^
+v-1< >92+0g"/"- 91+0g"/"- 90+0g"/"- v
+>:#v_90g"0"-70g` ^
+v-1< @ ... ... ... ... ...<
+>:#v_96+0g97+0g98+0g++51g-!!70g9-!+ ^
+v89<
+>+0g99+0g91+0g++51g-!!90g"0"-70g`!!+ ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_068_description.md b/www/statics/euler/euler_068_description.md
new file mode 100644
index 0000000..cb8dcca
--- /dev/null
+++ b/www/statics/euler/euler_068_description.md
@@ -0,0 +1,26 @@
+Consider the following "magic" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.
+
+
+
+Working clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example), each solution can be described uniquely.
+For example, the above solution can be described by the set: `4,3,2; 6,2,1; 5,1,3`.
+
+It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.
+
+Total | Solution Set
+------|------------------------
+9 | `4,2,3; 5,3,1; 6,1,2`
+9 | `4,3,2; 6,2,1; 5,1,3`
+10 | `2,3,5; 4,5,1; 6,1,3`
+10 | `2,5,3; 6,3,1; 4,1,5`
+11 | `1,4,6; 3,6,2; 5,2,4`
+11 | `1,6,4; 5,4,2; 3,2,6`
+12 | `1,5,6; 2,6,4; 3,4,5`
+12 | `1,6,5; 3,5,4; 2,4,6`
+
+By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is `432621513`.
+
+Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings.
+What is the maximum 16-digit string for a "magic" 5-gon ring?
+
+
\ No newline at end of file
diff --git a/www/statics/euler/euler_068_explanation.md b/www/statics/euler/euler_068_explanation.md
new file mode 100644
index 0000000..e9a5449
--- /dev/null
+++ b/www/statics/euler/euler_068_explanation.md
@@ -0,0 +1,16 @@
+The solution to this problem is similar to problem-043.
+We iterate through all possible 10-digit combinations but abort most paths pretty early through a few rules.
+This leads to a pretty quick execution time an a not so big program.
+
+I even managed to squeeze all in only half the available width so the other half has space enough for an ASCII representation of the magic 5-gon ring :D.
+*(You can see the result in the `problem-068 (visual)` file)*
+
+The main piece (excluding the act of pressing everything in such a small space) was formulating the rules.
+The more (an the earlier triggering) rules, the less paths we have to traverse and the faster our program gets:
+*(I needed to index the elements of the ring, so I went clockwise from the outermost to the inner elements.*
+
+The rules are:
+ - `N_3 > N_0`, `N_5 > N_0`, `N_7 > N_0`, `N_9 > N_0`. We want `N_0` to be the smallest element to avoid getting the same solution multiple times, only rotated. (Also it is stated that we start counting from the smallest outer element)
+ - `N_0 <= 5`, otherwise it can't be the smallest outer element
+ - `N_1 <> 9`, `N_2 <> 9`, `N_4 <> 9`, `N_6 <> 9`, `N_8 <> 9`, otherwise we won't get an 16-digit number
+ - `N_2+N_3+N_4 = N_0+N_1+N_2`, `N_4+N_5+N_6 = N_0+N_1+N_2`, `N_6+N_7+N_8 = N_0+N_1+N_2`, `N_8+N_9+N_1 = N_0+N_1+N_2`. Our condition for the ring to be "magic"
\ No newline at end of file
diff --git a/www/statics/euler/euler_069.php b/www/statics/euler/euler_069.php
new file mode 100644
index 0000000..57e6dee
--- /dev/null
+++ b/www/statics/euler/euler_069.php
@@ -0,0 +1,19 @@
+ 69,
+ 'title' => 'Totient maximum',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_069_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_069_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_069_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=069',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-069.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 35542,
+ 'time' => 16,
+ 'width' => 80,
+ 'height' => 10,
+ 'value' => 510510,
+];
diff --git a/www/statics/euler/euler_069_code.txt b/www/statics/euler/euler_069_code.txt
new file mode 100644
index 0000000..59c4c17
--- /dev/null
+++ b/www/statics/euler/euler_069_code.txt
@@ -0,0 +1,10 @@
+v000000 // Project Euler - Problem 69
+################################################################################
+################################################################################
+################################################################################
+v >p50g1+50pv @.g07<
+v ^1g0< >30g1+:30p40g- #v_"}}@"**60p 0>:1g70g*v$
+>170p"P":10p3:20p*40p230pv^5g03_^#-" "g+1/g01\%g01:g03g` |
+>"X"30g:10g%\10g/1+p30g>30g+:40g\` #v_$>30g1+:30p:10g%\10g/1+g" "-|^ p07<
+ ^p+1/g01\%g01:\" ":< ^ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_069_description.md b/www/statics/euler/euler_069_description.md
new file mode 100644
index 0000000..12a8e9b
--- /dev/null
+++ b/www/statics/euler/euler_069_description.md
@@ -0,0 +1,19 @@
+Euler's Totient function, `phi(n)` (sometimes called the phi function),
+is used to determine the number of numbers less than n which are relatively prime to n.
+For example, as 1, 2, 4, 5, 7, and 8, are all less than nine and relatively prime to nine, `phi(9)=6`.
+
+n | Relatively Prime | phi(n) | n/phi(n)
+---|------------------|--------|-------
+2 | 1 | 1 | 2
+3 | 1,2 | 2 | 1.5
+4 | 1,3 | 2 | 2
+5 | 1,2,3,4 | 4 | 1.25
+6 | 1,5 | 2 | 3
+7 | 1,2,3,4,5,6 | 6 | 1.1666...
+8 | 1,3,5,7 | 4 | 2
+9 | 1,2,4,5,7,8 | 6 | 1.5
+10 | 1,3,7,9 | 4 | 2.5
+
+It can be seen that n=6 produces a maximum `n/phi(n)` for `n <= 10`.
+
+Find the value of `n <= 1,000,000` for which `n/phi(n)` is a maximum.
\ No newline at end of file
diff --git a/www/statics/euler/euler_069_explanation.md b/www/statics/euler/euler_069_explanation.md
new file mode 100644
index 0000000..6a3bba0
--- /dev/null
+++ b/www/statics/euler/euler_069_explanation.md
@@ -0,0 +1,3 @@
+I had a really complicated solution where I tried to generate an Phi Sieve and had to work around a lot of corner cases.
+Then I looked at [this](http://www.mathblog.dk/project-euler-69-find-the-value-of-n-%E2%89%A4-1000000-for-which-n%CF%86n-is-a-maximum/) solution and - well - it's faster and simpler than mine.
+So I translated it to befunge.
\ No newline at end of file
diff --git a/www/statics/euler/euler_070.php b/www/statics/euler/euler_070.php
new file mode 100644
index 0000000..a7efd5d
--- /dev/null
+++ b/www/statics/euler/euler_070.php
@@ -0,0 +1,19 @@
+ 70,
+ 'title' => 'Totient permutation',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_070_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_070_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_070_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=070',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-070.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 29380799,
+ 'time' => 3713,
+ 'width' => 150,
+ 'height' => 47,
+ 'value' => 8319823,
+];
diff --git a/www/statics/euler/euler_070_code.txt b/www/statics/euler/euler_070_code.txt
new file mode 100644
index 0000000..6b3c283
--- /dev/null
+++ b/www/statics/euler/euler_070_code.txt
@@ -0,0 +1,17 @@
+v00000 000 // Project Euler - Problem 70
+ ccc
+ ?? ?? ??
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>55*6*:10p57*:20p*40p230p"2("*11p"}("*21p022p112p"}22 "***31p1v>030p v>g 0\v v\-1 < >g 0\v v\-1 <
+vp08*8**::**::8p31p30:" " _^#`g03g04< 2 v+55:<>\1>9*\:| 2 v+55:<>\1>9*\:|
+>"X"30g:10g%\10g/3+p30g>30g+:40g\` #v_$>30g1+:30p:10g%\10g/3+g" "-| 7 >%\:#^|#/+55\$< 8 >%\:#^|#/+55\$<
+ ^p+3/g01\%g01:\" ":< ^ < >$ #\>#<>\# :#+_+^>$ #\>#<>\# :#+_vv
+vg11 <^ < v -+<-
+>:42p::10g%\10g/3+g"X"-#v_:1+>:52p::10g%\10g/3+g"X"-#v_42g52g*:72p31g`#v_72g22g*42g1-52g1-*:82p12g*`#v_^v_v
+ >$12g.@ v $< < v < <
+^_^#-g12:+1 < <^_^#-g12:+1 < 71,
+ 'title' => 'Ordered fractions',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_071_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_071_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_071_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=071',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-071.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 77428679,
+ 'time' => 11981,
+ 'width' => 73,
+ 'height' => 8,
+ 'value' => 428570,
+];
diff --git a/www/statics/euler/euler_071_code.txt b/www/statics/euler/euler_071_code.txt
new file mode 100644
index 0000000..ecddef7
--- /dev/null
+++ b/www/statics/euler/euler_071_code.txt
@@ -0,0 +1,8 @@
+v X X C
+ X X ????
+
+>020p040p121p141p"}}@"**60pv
+v0 < >01+*v
+>1+ :3*7%!#v_:61p:3*7/:71p7*61g3*-:0`| >81p61g7*91p41g91g*21g81g*`#v_v
+|-g06: < <>01-*^v p04g16p02g17p12g19p14g18<
+>$20g."/ ",,55+,40g.@ ^ < <
\ No newline at end of file
diff --git a/www/statics/euler/euler_071_description.md b/www/statics/euler/euler_071_description.md
new file mode 100644
index 0000000..3f28de2
--- /dev/null
+++ b/www/statics/euler/euler_071_description.md
@@ -0,0 +1,12 @@
+Consider the fraction, `n/d`, where `n` and `d` are positive integers. If `n 72,
+ 'title' => 'Counting fractions',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_072_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_072_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_072_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=072',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-072.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 339636085,
+ 'time' => 50606,
+ 'width' => 486,
+ 'height' => 1047,
+ 'value' => 303963552391,
+];
diff --git a/www/statics/euler/euler_072_code.txt b/www/statics/euler/euler_072_code.txt
new file mode 100644
index 0000000..7a36020
--- /dev/null
+++ b/www/statics/euler/euler_072_code.txt
@@ -0,0 +1,24 @@
+v00000 // Project Euler - Problem 72
+ XX |AAAAAAAAAAAAAAAAAAA|
+ OOOO
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>699**:10p3777***:20p*40p230p" ":03p13p"}}@"**11p192*+21p022pv >030p0>::10g%\10g/3+g"X"-#v_v
+vp+3/g01\%g01:\"#":-1 :| ^ <>\10g/3+pv
+v $<0 _^#`g03g04<|-g04:+1 < <
+>"X"30g:10g%\10g/3+p30g>30g+:40g\` #v_$>30g1+:30p:10g%\10g/3+g" "-|$
+ > v ^p+3/g01\%g01:\" ":< ^ <
+v_^#!:p1+9\" ":-1$091pv v p23*g23-1p24*<
+v < 42g11g`#v_32g12g42g1--+12p>21g1-22g`22g9+1g:10g%\10g/3+g42g*11g`!*|>9+1g:10g%\10g/3+g*11g`!*|
+ > ^vg01:g1+9g22p24/g+3/g01\%g01:g1+9g22g24<^g22g24`g1+9g22g05%\10g/3+g22g0`22g9+1g22g8+1g-!*!-32g\/32p22g9+1g1+22g9+1p^g
+ >*!-32g\/32p22g9+1g1+22g9+1p #@ #. #g #2 #1 #< ^9
+ ^!-g1+8g22g1+9g22`0g22p24/\g24:g+3/g01\%g01:g1+9g22_^#!`p22:-1g220p1+<
\ No newline at end of file
diff --git a/www/statics/euler/euler_072_description.md b/www/statics/euler/euler_072_description.md
new file mode 100644
index 0000000..d8ccdf3
--- /dev/null
+++ b/www/statics/euler/euler_072_description.md
@@ -0,0 +1,12 @@
+Consider the fraction, `n/d`, where `n` and `d` are positive integers.
+If `n limit`. Because every other factor will only increase `x`.
+ - The value of phi is always calculated from the last phi value. So we don't need to totally recalculate it in every step.
+
+After looking a little bit around this is not ***the** fastest solution to this problem.
+But it's the one I found and I think it's reasonable fast.
\ No newline at end of file
diff --git a/www/statics/euler/euler_073.php b/www/statics/euler/euler_073.php
new file mode 100644
index 0000000..6d1f5ac
--- /dev/null
+++ b/www/statics/euler/euler_073.php
@@ -0,0 +1,19 @@
+ 73,
+ 'title' => 'Counting fractions in a range',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_073_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_073_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_073_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=073',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-073.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 1281174401,
+ 'time' => 202458,
+ 'width' => 2000,
+ 'height' => 12010,
+ 'value' => 7295372,
+];
diff --git a/www/statics/euler/euler_073_code.txt b/www/statics/euler/euler_073_code.txt
new file mode 100644
index 0000000..de8f5f2
--- /dev/null
+++ b/www/statics/euler/euler_073_code.txt
@@ -0,0 +1,14 @@
+v // Project Euler - Problem 73
+ XX ????
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>"}`"*11p051p0v
+vp12*"(2" < v+1 < <
+>1+:1+2/61p:71p:3/1+>:61g\`!#v_:21g%71g3+g!|>81g11g`91g11g`+#^_081g21gv
+|-g11: >#$ #< ^p19+g19g17p18+g18:p+3g19%<
+>$51g.@ ^p19g17p18:p15+1g15<
\ No newline at end of file
diff --git a/www/statics/euler/euler_073_description.md b/www/statics/euler/euler_073_description.md
new file mode 100644
index 0000000..de76bd0
--- /dev/null
+++ b/www/statics/euler/euler_073_description.md
@@ -0,0 +1,11 @@
+Consider the fraction, `n/d`, where n and d are positive integers. If `n 74,
+ 'title' => 'Digit factorial chains',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_074_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_074_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_074_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=074',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-074.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 376912541,
+ 'time' => 49187,
+ 'width' => 1224,
+ 'height' => 833,
+ 'value' => 402,
+];
diff --git a/www/statics/euler/euler_074_code.txt b/www/statics/euler/euler_074_code.txt
new file mode 100644
index 0000000..a73c070
--- /dev/null
+++ b/www/statics/euler/euler_074_code.txt
@@ -0,0 +1,21 @@
+v X ########## // Project Euler - Problem 74
+ CCC
+ XXXX |------------------------------------------------------------|
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>98+8*9*11p"+&"*2/21p"}}@"**31p042p31g>1-:0\:11g%v
+vg11:-8*:+"W~"2p+4/g11\%g11:/3*"'C"2p<|:p+4/g11\ < v <
+%>8-:11g%\11g/4+p3",!"*2+:11g%\11g/4+^$ >:70g:1+70p9 +0v
+\^**"CCQ"3p+4/g11\%g11:+"+~"3p+4/g11\<>070p11|-+55g07*g07 p<^ p22+g22_v
+>11g/4+p2"m"8*:11g%\11g/4+ v ^%g11:00< # >:55+%9+0v>11g/4+g: ^$
+v1$p+4/g11\%g11:-7*:+"W~"2p<>12g22g1+:22p9+2p32g1+32p12g0\:|:/+55\g <^\%g11:g21<
+>:12p022p092p032p32g9+2g12g-|-g21g2+9g23 <>$>\# :#+_+:12p31g`!|
+ v < <^ <<
++>22g"<"-#v_42g1+42p>1>:9+2g31g`#v_::22g1+\-\9+2v
+1 >$42g.@ > ^ ^+1_v#-g23: 363601 -> 1454 -> 169
+871 -> 45361 -> 871
+872 -> 45362 -> 872
+~~~
+
+It is not difficult to prove that EVERY starting number will eventually get stuck in a loop. For example,
+
+~~~
+69 -> 363600 -> 1454 -> 169 -> 363601 (-> 1454)
+78 -> 45360 -> 871 -> 45361 (-> 871)
+540 -> 145 (-> 145)
+~~~
+
+Starting with 69 produces a chain of five non-repeating terms,
+but the longest non-repeating chain with a starting number below one million is sixty terms.
+
+How many chains, with a starting number below one million, contain exactly sixty non-repeating terms?
\ No newline at end of file
diff --git a/www/statics/euler/euler_074_explanation.md b/www/statics/euler/euler_074_explanation.md
new file mode 100644
index 0000000..75db85e
--- /dev/null
+++ b/www/statics/euler/euler_074_explanation.md
@@ -0,0 +1,9 @@
+The factorial part is pretty easy - we cache the factorials from 1 to 9 and then we can calculate `facdigitsum(n)` in `O(log_10(n))`.
+
+The problemdescription tells us there are only seven numbers in a loop (`{169, 363601, 1454}`, `{871, 45361}`, `{872, 45362}`).
+So every other chain ends with a number mapping to itself. We manually insert these seven numbers in our grid and calculate the rest (where we only need to test if `f(n) == f(n-1)`).
+
+And we cache ever calculated value of `chainlength()` in our 1000000-element array. So as soon as we reach an already calculated number we can stop.
+This works because there are no loops (except the seven pre-inserted values) and every chain is strictly linear.
+
+Be sure to check out the pre-optimized version of this to see just how much more condensed this version is :)
\ No newline at end of file
diff --git a/www/statics/euler/euler_075.php b/www/statics/euler/euler_075.php
new file mode 100644
index 0000000..6480a3d
--- /dev/null
+++ b/www/statics/euler/euler_075.php
@@ -0,0 +1,19 @@
+ 75,
+ 'title' => 'Singular integer right triangles',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_075_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_075_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_075_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=075',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-075.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 293080647,
+ 'time' => 39951,
+ 'width' => 1000,
+ 'height' => 1515,
+ 'value' => 161667,
+];
diff --git a/www/statics/euler/euler_075_code.txt b/www/statics/euler/euler_075_code.txt
new file mode 100644
index 0000000..46a5dea
--- /dev/null
+++ b/www/statics/euler/euler_075_code.txt
@@ -0,0 +1,20 @@
+v XX O OO // Project Euler - Problem 75
+ AAA A A
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+
+> "}"8* 20p "}}`"** 30p 30g>:0\:20g%\20v
+v p060$_^#!\-1:p+3/g<
+ v p08+1g08<
+>180p>80g::*4*\6*2++30g`#v_>80g1+:90p>::2**\80g2**+30g` |
+ @.g06< ^p09:+1g09<
+v g13g12p16++p14:+*:g08*:g09p13:**2g09g08p12:-*:g08*:g09<
+>`#v_ >1>:61g*30g`#v_:21g7*31g+5*41g+# *81p:61g*:20g%\20g/3+g:#v_v
+ >21g31g21p31p^ ^+1 <># $# ^# _v#<`\0_v#-g18:<
+ ^p06-1g06p+3/g02\%g02:\-10*g16: 76,
+ 'title' => 'Counting summations',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_076_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_076_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_076_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=076',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-076.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 296178,
+ 'time' => 32,
+ 'width' => 104,
+ 'height' => 108,
+ 'value' => 190569291,
+];
diff --git a/www/statics/euler/euler_076_code.txt b/www/statics/euler/euler_076_code.txt
new file mode 100644
index 0000000..ea39ca4
--- /dev/null
+++ b/www/statics/euler/euler_076_code.txt
@@ -0,0 +1,12 @@
+v X OO // Project Euler - Problem 76
+v
+v
+ + ... +
+ . . . .
+ . . .
+ . . . .
+ + ... +
+
+ v+1 p:+3\+1g06:$< > :50g\-3v
+>"d"30p1>:30g`#v_:50p060p1>:50g-!#^_::::50g\-`#^_: 3v
+ >1+:1+g.@ ^+1p+3g05+3\p06:+g06g+3-\g05\+<
\ No newline at end of file
diff --git a/www/statics/euler/euler_076_description.md b/www/statics/euler/euler_076_description.md
new file mode 100644
index 0000000..1e2634a
--- /dev/null
+++ b/www/statics/euler/euler_076_description.md
@@ -0,0 +1,12 @@
+It is possible to write five as a sum in exactly six different ways:
+
+~~~
+4 + 1
+3 + 2
+3 + 1 + 1
+2 + 2 + 1
+2 + 1 + 1 + 1
+1 + 1 + 1 + 1 + 1
+~~~
+
+How many different ways can one hundred be written as a sum of at least two positive integers?
\ No newline at end of file
diff --git a/www/statics/euler/euler_076_explanation.md b/www/statics/euler/euler_076_explanation.md
new file mode 100644
index 0000000..c7e3223
--- /dev/null
+++ b/www/statics/euler/euler_076_explanation.md
@@ -0,0 +1,44 @@
+The big trick is - similar to many other problems - *caching*.
+
+This problem remembered me a little bit of problem-15.
+We use a `100x100` grid to remember pre-calculated sums.
+
+So in cell [3, 6] is the amount of sums which result in `6`, start with `3` and have all summands in descending order:
+
+~~~
+3 + 3
+3 + 2 + 1
+3 + 1 + 1
+~~~
+
+You see `cache[3,6] = 3`.
+
+Now to find a new value (for example `[4, 7]`) we just have to look at the our cache:
+
+~~~
+7 = 4 + x
+sum(x) = 7-4 = 3
+
+// first_digit_of_x <= first_digit, because of the descending order
+sum(x) = sum([n, 3]); n = [1..3]
+sum(x) = [3, 3] + [2, 3] + [1, 3]
+~~~
+
+You see it's important not only to remember the amount but also the first (= highest) summand,
+so we can guarantee the oder of the sums (an this way that we don't count any sums multiple times).
+
+*Note:* `cache[a, a]` is always `1`. But the problem rules dictate that when we calculate the final result we must ignore this (`100 = 100` is not a valid solution)
+
+Oh and this algorithm improves the native approach (enumerating all solutions) from `O(wtf)` to `O(n^2)`.
+I'm not sure if I would be still alive when my first algorithm finishes :)
+
+----
+
+**Edit:**
+
+I did a little optimization:
+
+The value of cell `[d, s]` is now the sum of all previous cells from `[0, s]` to `[d, s]`.
+
+This way we don't have to iterate through all the cells from 0 to d every time.
+We can just look at the biggest cell which contains the sum of all previous.
\ No newline at end of file
diff --git a/www/statics/euler/euler_077.php b/www/statics/euler/euler_077.php
new file mode 100644
index 0000000..b73b950
--- /dev/null
+++ b/www/statics/euler/euler_077.php
@@ -0,0 +1,19 @@
+ 77,
+ 'title' => 'Prime summations',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_077_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_077_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_077_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=077',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-077.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 312139,
+ 'time' => 47,
+ 'width' => 101,
+ 'height' => 39,
+ 'value' => 71,
+];
diff --git a/www/statics/euler/euler_077_code.txt b/www/statics/euler/euler_077_code.txt
new file mode 100644
index 0000000..2fbaac8
--- /dev/null
+++ b/www/statics/euler/euler_077_code.txt
@@ -0,0 +1,19 @@
+v00000 00 // Project Euler - Problem 77
+ XXXXXX
+# ... #
+
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+> "e" :10p 1 :20p*40p230p" ":02p12pvv03:+1g03< >030p 0>::10g%\10g/2+g"X"-#v_:30g:1+30p:v
+v <># p# :# v# _^#`g03g04<|-g04:+1 "X"30g:10g%\10g/2+p30g>30g+:40g\` #v_$^>10g%\10g/2+g" "-|>$30g:50p10g*>1-:0\:10g%\10g/4+pv
+ ^p+2/g01\%g01:\" ":< ^ < ^_v#: <
+vp08"d"p07*"}("$ <
+0 >061p31g>:0\`#v_:4+51g\g61g+61pv
+>1+:11p021p031p>31g:50g-\2g:41p11g`!*!#v_11g41g-:51p| ^-1 <
+^ _v#!`g07g12< >111g31g4+pv >$21g61g:1v
+ ^ ># 1# 1# g# .# @# p13+1g13 78,
+ 'title' => 'Coin partitions',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_078_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_078_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_078_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=078',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-078.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 1191633332,
+ 'time' => 170946,
+ 'width' => 251,
+ 'height' => 256,
+ 'value' => 55374,
+];
diff --git a/www/statics/euler/euler_078_code.txt b/www/statics/euler/euler_078_code.txt
new file mode 100644
index 0000000..536b4ce
--- /dev/null
+++ b/www/statics/euler/euler_078_code.txt
@@ -0,0 +1,11 @@
+vXX OOO
+ # ... #
+ . . . .
+ . . .
+ . . . .
+ # ... #
+
+ >$.@
+ v+1p+1/g01\+1%g01:g04_^#:%g02g05$$ <
+>"}}@"**20p"~|"+10p111p1>:40p050p0>:60p::2/1+:*3*\:2/1+\2%2*1-*+2/:40g`#^_4 v
+ ^+1p05-\g05*-1*2%2/2g06g+1/g01\+1%g01:-\g0<
\ No newline at end of file
diff --git a/www/statics/euler/euler_078_description.md b/www/statics/euler/euler_078_description.md
new file mode 100644
index 0000000..305ac84
--- /dev/null
+++ b/www/statics/euler/euler_078_description.md
@@ -0,0 +1,14 @@
+Let `p(n)` represent the number of different ways in which n coins can be separated into piles.
+For example, five coins can be separated into piles in exactly seven different ways, so `p(5)=7`.
+
+~~~
+OOOOO
+OOOO O
+OOO OO
+OOO O O
+OO OO O
+OO O O O
+O O O O O
+~~~
+
+Find the least value of n for which p(n) is divisible by one million.
\ No newline at end of file
diff --git a/www/statics/euler/euler_078_explanation.md b/www/statics/euler/euler_078_explanation.md
new file mode 100644
index 0000000..4ba2648
--- /dev/null
+++ b/www/statics/euler/euler_078_explanation.md
@@ -0,0 +1,4 @@
+Again the algorithm is from [MathBlog](http://www.mathblog.dk/project-euler-78-coin-piles/).
+I can't really say that I understand the algorithm fully (and the MathBlog guy says he neither).
+
+But for the best explanation you better read his article.
\ No newline at end of file
diff --git a/www/statics/euler/euler_079.php b/www/statics/euler/euler_079.php
new file mode 100644
index 0000000..198a429
--- /dev/null
+++ b/www/statics/euler/euler_079.php
@@ -0,0 +1,19 @@
+ 79,
+ 'title' => 'Passcode derivation',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_079_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_079_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_079_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=079',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-079.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 12040,
+ 'time' => 0,
+ 'width' => 56,
+ 'height' => 21,
+ 'value' => 73162890,
+];
diff --git a/www/statics/euler/euler_079_code.txt b/www/statics/euler/euler_079_code.txt
new file mode 100644
index 0000000..84c8780
--- /dev/null
+++ b/www/statics/euler/euler_079_code.txt
@@ -0,0 +1,21 @@
+v
+ ++++++++++ 319 680 180 690 129 620 762 689 762 318
+ ++++++++++ 368 710 720 710 629 168 160 689 716 731
+ ++++++++++ 736 729 316 729 729 710 769 290 719 680
+ ++++++++++ 318 389 162 289 162 718 729 319 790 680
+ ++++++++++ 890 362 319 760 316 729 380 319 728 716
+ ++++++++++
+ ++++++++++ ##########
+ ++++++++++
+ ++++++++++ XXXXXXXXXX
+ ++++++++++
+
+>55+>:1\:v>:55+/1+30p:55+%4*66++20p020g0+30gg"0"-:50p66v
+ |:-1p< v1g070p+1g07+1g062p+1g07+1g052p+1g06+1g052< +
+ >$ 77*^>+50g1+p070g1+60g1vv< < p +
+ |\-1:p+1g05+1g060p+<1|!\-1: # $# 0# 9# 0# p# 9#<>:66++7g#^_ :90g:1+9^ + p
+ >:90g-!#v_:::66++9g1+\65++9g1+g*!#^_::v + 0
+ ^p9++66\ g02:-1p9++66\g9++56p02g9++66:< 6 2
+ >$0>:66++9g. v >020g2+30gg"0"-:70p6^ 0
+ @$_^#!-g09:+1< ^p7++66p06:-"0"gg03+1g<
\ No newline at end of file
diff --git a/www/statics/euler/euler_079_description.md b/www/statics/euler/euler_079_description.md
new file mode 100644
index 0000000..1ec757d
--- /dev/null
+++ b/www/statics/euler/euler_079_description.md
@@ -0,0 +1,16 @@
+A common security method used for online banking is to ask the user for three random characters from a passcode.
+For example, if the passcode was 531278, they may ask for the 2nd, 3rd, and 5th characters;
+the expected reply would be: 317.
+
+The text file, keylog.txt, contains fifty successful login attempts.
+
+~~~
+319 680 180 690 129 620 762 689 762 318
+368 710 720 710 629 168 160 689 716 731
+736 729 316 729 729 710 769 290 719 680
+318 389 162 289 162 718 729 319 790 680
+890 362 319 760 316 729 380 319 728 716
+~~~
+
+Given that the three characters are always asked for in order,
+analyse the file so as to determine the shortest possible secret passcode of unknown length.
\ No newline at end of file
diff --git a/www/statics/euler/euler_079_explanation.md b/www/statics/euler/euler_079_explanation.md
new file mode 100644
index 0000000..4f8a9c0
--- /dev/null
+++ b/www/statics/euler/euler_079_explanation.md
@@ -0,0 +1,20 @@
+This is one of the problems i really enjoyed solving.
+
+We make the assumption that our final pass code has no duplicate digits (If we hadn't found a solution we would need to change that part).
+This is a pretty good assumption because no attempt has a duplicate digit in it.
+
+> *Side note:* This leaves us with a 8-digit code, because only 8 digits are used (`4` and `5` are missing).
+
+First we generate a 10x10 grid where we remember the absolute ordering of the numbers from our attempts (eg `3` is before `8` or `9` is after `2`).
+If we inspect this data we can see that every field (for numbers in our pass code) is set, the fifty login attempts generate more than enough data for this.
+
+> *Side note:* In fact there are only 33 **unique** login attempts
+
+Then we can simply sort an array of the valid digits with this ordering. And - frankly - I find this is a really neat way of doing this.
+
+Because we sort only eight numbers, sorting-performance is not a big factor.
+So I searched for the simplest (easiest to implement) sorting algorithm I could find.
+This was surprisingly not Bubble-sort, but [Gnome Sort](https://en.wikipedia.org/wiki/Gnome_sort) (accordingly to the author "the simplest sort algorithm").
+Which was pretty easy to implement in Befunge (and for 8 values is the runtime of O(n^2) not *that* bad).
+
+A last thing: For a problem where I used an two-dimensional cache **and** that has input data I was surprised to fit everything in the Befunge-93 80x25 size restrictions.
diff --git a/www/statics/euler/euler_080.php b/www/statics/euler/euler_080.php
new file mode 100644
index 0000000..39873d7
--- /dev/null
+++ b/www/statics/euler/euler_080.php
@@ -0,0 +1,19 @@
+ 80,
+ 'title' => 'Square root digital expansion',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_080_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_080_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_080_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=080',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-080.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 540417723,
+ 'time' => 116439,
+ 'width' => 69,
+ 'height' => 18,
+ 'value' => 40886,
+];
diff --git a/www/statics/euler/euler_080_code.txt b/www/statics/euler/euler_080_code.txt
new file mode 100644
index 0000000..5eb9d79
--- /dev/null
+++ b/www/statics/euler/euler_080_code.txt
@@ -0,0 +1,18 @@
+v X X XX X
+ ############################################################
+
+ @ ############################################################
+ .
+ g ############################################################
+ 0
+ ^9$># #< v v < v <
+ $ v_^#-"d"\+1:< <>$"<">1-::9+5g\9+1p:#^_$0>:::9+3g55+%55+*v
+>090p2>:20p"d">::*20g-#v_$^|!:-1p5+8\-g07g06p04 # <\
+ # v"<":$_^# !:-1< >::9+1g40g-60p:9+3g20g45***70p0>70g60g`!|5
+ ^ <>1-:0\9+1p:0\v ^ ";"p04* :g02p5"D"0p<#+ 65
+ |:p5+9\0:p3+9< >9+1g-!#v_::9+5g\9+1g`!#v_$20g1-20^ 1 0+
+ >$"D"1p"d"020p>20g:*40p "<">1-::9+3g20g 45***40gv ^p06+"d"g<+
+ ^ _> #v^#-"<":+1< |:p5+9\%"d"p 04/"d":+#<# ^# < > ";"-|
+ ^ !:-1p020p09+g09g02p3"D"+g02*+55%+55g3"D"$<
\ No newline at end of file
diff --git a/www/statics/euler/euler_080_description.md b/www/statics/euler/euler_080_description.md
new file mode 100644
index 0000000..25e9324
--- /dev/null
+++ b/www/statics/euler/euler_080_description.md
@@ -0,0 +1,8 @@
+It is well known that if the square root of a natural number is not an integer, then it is irrational.
+The decimal expansion of such square roots is infinite without any repeating pattern at all.
+
+The square root of two is `1.41421356237309504880...`,
+and the digital sum of the first one hundred decimal digits is `475`.
+
+For the first one hundred natural numbers,
+find the total of the digital sums of the first one hundred decimal digits for all the irrational square roots.
\ No newline at end of file
diff --git a/www/statics/euler/euler_080_explanation.md b/www/statics/euler/euler_080_explanation.md
new file mode 100644
index 0000000..98b48c2
--- /dev/null
+++ b/www/statics/euler/euler_080_explanation.md
@@ -0,0 +1,27 @@
+A short look to [Wikipedia](https://en.wikipedia.org/wiki/Methods_of_computing_square_roots#Digit-by-digit_calculation) finds us a neat algorithm to calculate the square-root digit-by-digit.
+
+I have optimized it a little bit with the target to use not so many variables:
+
+~~~
+IEnumerable DRoot(int r)
+{
+ BigInteger c = r;
+ BigInteger p = 0;
+ int x = 0;
+
+ for (ii = 0; ii < 100; ii++)
+ {
+ for (x = 0;(x+1)*(20*p + (x+1)) <= c;x++);
+ c = 100*c - 2000*p*x - 100*x*x;
+ p = p*10 + x;
+ }
+
+ return p;
+}
+~~~
+
+The algorithm is pretty simple, but *god* do I hate long addition/multiplication in Befunge.
+
+We need 120 base-10 digits for the numbers `p`and `c`.
+In our program we use base-100 notation. This way we can fit the numbers in a single befunge-93 row
+**and** can simply multiply by 100 with a single left shift operation.
\ No newline at end of file
diff --git a/www/statics/euler/euler_081.php b/www/statics/euler/euler_081.php
new file mode 100644
index 0000000..d0b3c86
--- /dev/null
+++ b/www/statics/euler/euler_081.php
@@ -0,0 +1,19 @@
+ 81,
+ 'title' => 'Path sum: two ways',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_081_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_081_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_081_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=081',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-081.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 1697244,
+ 'time' => 234,
+ 'width' => 500,
+ 'height' => 180,
+ 'value' => 427337,
+];
diff --git a/www/statics/euler/euler_081_code.txt b/www/statics/euler/euler_081_code.txt
new file mode 100644
index 0000000..795561d
--- /dev/null
+++ b/www/statics/euler/euler_081_code.txt
@@ -0,0 +1,25 @@
+v 4445 2697 5115 ... 5870
+ 1096 0020 1318 ... 9377
+ # ... # 9607 7385 0521 ... 9230
+ . . . . 7206 3114 7760 ... 2187
+ . . . 3620 8024 0577 ... 7505
+ . . . . 1074 5438 9008 ... 6942
+ # ... # 4295 1176 5596 ... 4757
+
+>"d@"*>1-:::::"P"%5*"g"+\"P"/g"0"-\::"P"%5*"f"+\"P"/g"0"-\::"P"%5*"e"+\"P"/g"0"-\: v
+ |:p+"d"/"P"\+9%"P":\*:*"~~"p+2/"P"\+9%"P":\+*+55+*+55+*+55-"0"g/"P"\+"d"*5%"P"<
+ $ >20g8+30g"d"v
+ >0>:20p 0>:30p20g9+30g2+g20g9+30g"c"+g20g8+30g"d"+g20g30g+!#v_20g!#v_30g!#v_`|
+ |-"P":+1p+"d"g03+9g02 < < < <>20g9+30g"c"v
+ |-"P":+1$< ^$$< ^+$< ^+$\< ^ +g+<
+ $
+ >"O"9+"Od"+g.@
+
+
+
+
+ # ... #
+ . . . .
+ . . .
+ . . . .
+ # ... #
\ No newline at end of file
diff --git a/www/statics/euler/euler_081_description.md b/www/statics/euler/euler_081_description.md
new file mode 100644
index 0000000..23e1225
--- /dev/null
+++ b/www/statics/euler/euler_081_description.md
@@ -0,0 +1,14 @@
+In the 5 by 5 matrix below, the minimal path sum from the top left to the bottom right,
+by only moving to the right and down, is indicated in bold red and is equal to 2427.
+
+~~~
+131 673 234 103 018
+201 096 342 965 150
+630 803 746 422 111
+537 699 497 121 956
+805 732 524 037 331
+~~~
+
+Find the minimal path sum, in matrix.txt (right click and "Save Link/Target As..."),
+a 31K text file containing a 80 by 80 matrix,
+from the top left to the bottom right by only moving right and down.
\ No newline at end of file
diff --git a/www/statics/euler/euler_081_explanation.md b/www/statics/euler/euler_081_explanation.md
new file mode 100644
index 0000000..1ef2bdb
--- /dev/null
+++ b/www/statics/euler/euler_081_explanation.md
@@ -0,0 +1,9 @@
+Well, this is practically extremely simple path finding.
+
+We generate an array where we remember the shortest distance from [0,0] to this node.
+Initially we can set `distance[0, 0] = data[0,0]`
+
+The we got through our data row by row and column by column.
+The distance of every node we visit is the minimum of `top-node-distance + own value` and `left-node-distance + own value`.
+
+Then after we iterated through every single node the result is written in the bottom right corner.
\ No newline at end of file
diff --git a/www/statics/euler/euler_082.php b/www/statics/euler/euler_082.php
new file mode 100644
index 0000000..7b1d4fb
--- /dev/null
+++ b/www/statics/euler/euler_082.php
@@ -0,0 +1,19 @@
+ 82,
+ 'title' => 'Path sum: three ways',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_082_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_082_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_082_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=082',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-082.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 13777233,
+ 'time' => 2106,
+ 'width' => 500,
+ 'height' => 180,
+ 'value' => 260324,
+];
diff --git a/www/statics/euler/euler_082_code.txt b/www/statics/euler/euler_082_code.txt
new file mode 100644
index 0000000..4a685de
--- /dev/null
+++ b/www/statics/euler/euler_082_code.txt
@@ -0,0 +1,27 @@
+v 4445 2697 5115 ... 5870
+ 1096 0020 1318 ... 9377
+ # ... # 9607 7385 0521 ... 9230
+ . . . . 7206 3114 7760 ... 2187
+ . . . 3620 8024 0577 ... 7505
+ . . . . 1074 5438 9008 ... 6942
+ # ... # 4295 1176 5596 ... 4757
+
+>"d@"*>1-:::::"P"%5*"g"+\"P"/g"0"-\::"P"%5*"f"+\"P"/g"0"-\::"P"%5*"e"+\"P"/g"0"-\: v
+ |:p+"d"/"P"\+9%"P":\*:*"~~"p+2/"P"\+9%"P":\+*+55+*+55+*+55-"0"g/"P"\+"d"*5%"P"<
+ $
+ >"P">1-::9\2+gv
+ |:p+"d"\9\< >$$v >v
+ >$1>:20p0>:30p20g8+30g"d"+g40p30g>:50p40g20g9+50g2+g+::40p20g9+50g"d"+g`| >20g8+30g"d"+g40p30g>:50p40g20g9+50g2+g+::40p20g9+50g"d"+g`|
+ ^ < |-"P":+1 p+"d"g05+9g02< $ |+1:-1 p+"d"g05+9g02<
+ |-"P":+1 ># ^# $<$ <
+ |-"P":+1$< >70v
+ >$"O"9+"Od"+g70p"O">1-:"X"\"d"+g:70g`!|
+ |: $<0p<
+ >$70g.@
+
+
+ # ... #
+ . . . .
+ . . .
+ . . . .
+ # ... #
\ No newline at end of file
diff --git a/www/statics/euler/euler_082_description.md b/www/statics/euler/euler_082_description.md
new file mode 100644
index 0000000..abe2cb1
--- /dev/null
+++ b/www/statics/euler/euler_082_description.md
@@ -0,0 +1,17 @@
+NOTE: This problem is a more challenging version of Problem 81.
+
+The minimal path sum in the 5 by 5 matrix below,
+by starting in any cell in the left column and finishing in any cell in the right column,
+and only moving up, down, and right, is indicated in red and bold; the sum is equal to `994`.
+
+~~~
+131 673 234 103 018
+201 096 342 965 150
+630 803 746 422 111
+537 699 497 121 956
+805 732 524 037 331
+~~~
+
+Find the minimal path sum, in matrix.txt (right click and "Save Link/Target As..."),
+a 31K text file containing a 80 by 80 matrix,
+from the left column to the right column.
\ No newline at end of file
diff --git a/www/statics/euler/euler_082_explanation.md b/www/statics/euler/euler_082_explanation.md
new file mode 100644
index 0000000..f59241a
--- /dev/null
+++ b/www/statics/euler/euler_082_explanation.md
@@ -0,0 +1,20 @@
+As the problem description states this is similar to problem-081.
+
+Again we generate an node-array where we remark the minimal distance from the left side to this node.
+Initially we can initialize the left column with its input values.
+(`distance[0, y] = data[0, y]`) and all the other nodes with an absurdly high number.
+
+Then we iterate through all remaining columns:
+
+For each column `x` we go all possible ways from the previous column. That means:
+ - Choose the start-row `y` (and do this for all possible start rows)
+ - Get the distance to reach this row by calculating `distance[x-1, y] + data[x, y]`
+ - Then go all the way up and down and calculate the distance on the way `distance[x-1, y] + data[x, y] + data[x, y - 1] + data[x, y - 2] ...`
+ - For each node where this distance is lesser than the current one we update distance array.
+ - *Optimization node:* Once we find a node where the distance is greater than a previous calculated we can stop further traversing the column (in this direction)
+
+At the end we have an distance array where each node is the minimal distance to reach this node from the left side.
+Our result is then the minimal value of the most-right column.
+
+*Note:* While problem-081 hat an time complexity of O(n) this one has one of O(n^2).
+But for an 80x80 array that's still fast enough and really not an problem.
\ No newline at end of file
diff --git a/www/statics/euler/euler_083.php b/www/statics/euler/euler_083.php
new file mode 100644
index 0000000..a124f7a
--- /dev/null
+++ b/www/statics/euler/euler_083.php
@@ -0,0 +1,19 @@
+ 83,
+ 'title' => 'Path sum: four ways',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_083_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_083_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_083_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=083',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-083.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 11718762,
+ 'time' => 1748,
+ 'width' => 500,
+ 'height' => 180,
+ 'value' => 425185,
+];
diff --git a/www/statics/euler/euler_083_code.txt b/www/statics/euler/euler_083_code.txt
new file mode 100644
index 0000000..5958ee6
--- /dev/null
+++ b/www/statics/euler/euler_083_code.txt
@@ -0,0 +1,28 @@
+v 4445 2697 5115 ... 5870
+ 1096 0020 1318 ... 9377
+ # ... # 9607 7385 0521 ... 9230
+ . . . . 7206 3114 7760 ... 2187
+ . . . 3620 8024 0577 ... 7505
+ . . . . 1074 5438 9008 ... 6942
+ # ... # 4295 1176 5596 ... 4757
+
+>"d@"*>1-:::::"P"%5*"g"+\"P"/g"0"-\::"P"%5*"f"+\"P"/g"0"-\::"P"%5*"e"+\"P"/g"0"-\: v
+ |:p+"d"/"P"\+9%"P":\*:*"~~"p+2/"P"\+9%"P":\+*+55+*+55+*+55-"0"g/"P"\+"d"*5%"P"< >70g40g8+50g"d"+p v
+ >$120p92g9"d"p"Xdd"p>0>:40p 0>:50p40g"d"+50g"d"+g"X"-#v_820p"O"40g"d"+50g"d"+p 40g0`40g8+50g"d"+g40g9+50g"d"+g40g8+50g2+g+:70p`*|
+ |-"P":+1 < v ^ |-"P":+1$< >70g40g9+50g"c"+p v
+ $ >50g0`40g9+50g"c"+g40g9+50g"d"+g40g9+50g1+g+:70p`*|
+ |p070g07< v "O"9+"Od"+g.@ >70g40g55++50g"d"+pv
+ >40g"P"-40g55++50g"d"+g40g9+50g"d"+g40g55++50g2+g+:70p`*|
+ v 70g40g9+50g"e"+p"X"v
+ >50g"P"-40g9+50g"e"+g40g9+50g"d"+g40g9+50g3+g+:70p`*|
+ ^ 84,
+ 'title' => 'Monopoly odds',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_084_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_084_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_084_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=084',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-084.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 146519794,
+ 'time' => 19203,
+ 'width' => 77,
+ 'height' => 20,
+ 'value' => 101524,
+];
diff --git a/www/statics/euler/euler_084_code.txt b/www/statics/euler/euler_084_code.txt
new file mode 100644
index 0000000..5145c48
--- /dev/null
+++ b/www/statics/euler/euler_084_code.txt
@@ -0,0 +1,20 @@
+v XX
+ ======================================== v < v<
+ ???????????????????????????????????????? v<< v<<<|-"!":<|-+98:<
+>040p"}}@"**58*v v _v# -1< v<10 v 10> v < <|<
+ v < 0 |:+<2?^#*4<2?^#$< ^<
+ >1-:2+0\1pv ^3< ^3< -
+ |: < >>>v >>>v v< >>>v >>>v >>>v 2
+v $< 12 v 12 v #^p04<+55$<01 v 01 v 01 v >v :
+>40g::2+1g1+\2+1p>#^?3>#^?3>++58*%:40p>#^?2>4*#^?2>+4*#^?2>+|>:56*-|
+| >4^v<>4^ #v< v<>3^ >3^ >3^
+>$58vv >>v >>>v ^ < < <
+: $ 01 v 01 v #>v >v >v >v >v >v #>v >v >v > v
+- >#^?2>4*#^?2>+ :|>1-:|>1 -:|>1-:|>1-:|>1-:|>1-:|>1-:|>1-:|>1-:| #
+1>1-::2v>3^ >3^ >55+v>56 +v>64*v>"'"v>5v >0v v < v >40g3- v
+ |:p2+ <>::1+2g2+1g\ 2+2g 2+1 g \` v>v # >62*v
+ >$v ^_v#:<-1p2\g 05+2 :-1 p 2+2\ g2+1 :: p 05 g 2+2:_^#>40g492*+-|
+ >0>:58* \`| >$22 g.32 g.4 2 g.@ >40g6%1+2/2*5*5+v$ >74*v
+ ^+1 < >#<^# ># ># ># ># ># ># #< > v
+^< < < < < $p04<
\ No newline at end of file
diff --git a/www/statics/euler/euler_084_description.md b/www/statics/euler/euler_084_description.md
new file mode 100644
index 0000000..a6bc6d0
--- /dev/null
+++ b/www/statics/euler/euler_084_description.md
@@ -0,0 +1,57 @@
+In the game, Monopoly, the standard board is set up in the following way:
+
+~~~
+GO A1 CC1 A2 T1 R1 B1 CH1 B2 B3 JAIL
+H2 C1
+T2 U1
+H1 C2
+CH3 C3
+R4 R2
+G3 D1
+CC3 CC2
+G2 D2
+G1 D3
+G2J F3 U2 F2 F1 R3 E3 E2 CH2 E1 FP
+~~~
+
+A player starts on the GO square and adds the scores on two 6-sided dice to determine the number of squares they advance in a clockwise direction.
+Without any further rules we would expect to visit each square with equal probability: `2.5%`.
+However, landing on G2J (Go To Jail), CC (community chest), and CH (chance) changes this distribution.
+
+In addition to G2J, and one card from each of CC and CH, that orders the player to go directly to jail,
+if a player rolls three consecutive doubles, they do not advance the result of their 3rd roll.
+Instead they proceed directly to jail.
+
+At the beginning of the game, the CC and CH cards are shuffled.
+When a player lands on CC or CH they take a card from the top of the respective pile and, after following the instructions, it is returned to the bottom of the pile.
+There are sixteen cards in each pile, but for the purpose of this problem we are only concerned with cards that order a movement;
+any instruction not concerned with movement will be ignored and the player will remain on the CC/CH square.
+
+Community Chest (2/16 cards):
+ - Advance to GO
+ - Go to JAIL
+Chance (10/16 cards):
+ - Advance to GO
+ - Go to JAIL
+ - Go to C1
+ - Go to E3
+ - Go to H2
+ - Go to R1
+ - Go to next R (railway company)
+ - Go to next R
+ - Go to next U (utility company)
+ - Go back 3 squares.
+
+The heart of this problem concerns the likelihood of visiting a particular square. That is, the probability of finishing at that square after a roll.
+For this reason it should be clear that, with the exception of G2J for which the probability of finishing on it is zero,
+the CH squares will have the lowest probabilities, as `5/8` request a movement to another square,
+and it is the final square that the player finishes at on each roll that we are interested in.
+We shall make no distinction between "Just Visiting" and being sent to JAIL, and we shall also ignore the rule about requiring a double to "get out of jail",
+assuming that they pay to get out on their next turn.
+
+By starting at GO and numbering the squares sequentially from 00 to 39 we can concatenate these two-digit numbers to produce strings that correspond with sets of squares.
+
+Statistically it can be shown that the three most popular squares, in order, are `JAIL (6.24%) = Square 10`, `E3 (3.18%) = Square 24`, and `GO (3.09%) = Square 00`.
+So these three most popular squares can be listed with the six-digit modal string: 102400.
+
+If, instead of using two 6-sided dice, two 4-sided dice are used, find the six-digit modal string.
\ No newline at end of file
diff --git a/www/statics/euler/euler_084_explanation.md b/www/statics/euler/euler_084_explanation.md
new file mode 100644
index 0000000..9d94739
--- /dev/null
+++ b/www/statics/euler/euler_084_explanation.md
@@ -0,0 +1,9 @@
+This is not really a mathematical problem (or at least not with my solution).
+
+All I did was implement the rules in my befunge program and run a randomized game for `1 000 000` turns.
+This is called an [Monte Carlo algorithm](https://en.wikipedia.org/wiki/Monte_Carlo_algorithm) and if we have enough runs it becomes pretty improbable to get a wrong result.
+
+Perhaps there are some fancy mathematical solutions out there, but this works too.
+
+A note to the befunge code: It got pretty messy because of all the decisions we have to implement for the different monopoly rules,
+but all we needed as storage was an 40-element array. So it wasn't that hard to fit it all in the 80x25 space.
\ No newline at end of file
diff --git a/www/statics/euler/euler_085.php b/www/statics/euler/euler_085.php
new file mode 100644
index 0000000..dde5e7a
--- /dev/null
+++ b/www/statics/euler/euler_085.php
@@ -0,0 +1,19 @@
+ 85,
+ 'title' => 'Counting rectangles',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_085_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_085_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_085_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=085',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-085.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 880151,
+ 'time' => 109,
+ 'width' => 35,
+ 'height' => 8,
+ 'value' => 2772,
+];
diff --git a/www/statics/euler/euler_085_code.txt b/www/statics/euler/euler_085_code.txt
new file mode 100644
index 0000000..94a25c7
--- /dev/null
+++ b/www/statics/euler/euler_085_code.txt
@@ -0,0 +1,8 @@
+vX
+ YY YY YY
+>"}}_!"+**:10p11p051p071p>10g71g`v
+ v*`g18g01`g14g151g-:0\`#v_0>-:11g`#v_11p41g5v
+>*81g+81v>0\^v+1g14$<#0p12*g1<
+^g17p14:># p#< ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_085_description.md b/www/statics/euler/euler_085_description.md
new file mode 100644
index 0000000..6a07886
--- /dev/null
+++ b/www/statics/euler/euler_085_description.md
@@ -0,0 +1,6 @@
+By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:
+
+
+
+Although there exists no rectangular grid that contains exactly two million rectangles,
+find the area of the grid with the nearest solution.
\ No newline at end of file
diff --git a/www/statics/euler/euler_085_explanation.md b/www/statics/euler/euler_085_explanation.md
new file mode 100644
index 0000000..10f3f93
--- /dev/null
+++ b/www/statics/euler/euler_085_explanation.md
@@ -0,0 +1,13 @@
+The key to solve this problem is effectively iterating through the permutations for a given width and height (`perms[w, h]`).
+
+First we look at the baseline with `width=1`. The basic case `perms[1,1]` is `1`.
+After that `perms[1,h] = perms[1,h-1] + h` (so we can iterate easily through all these solutions).
+
+With the baseline in place we can see that `perms[w, h] = perms[w, h-1] + perms[w, 1] * h`.
+
+Then we just iterate through all the possibilities and search for the smallest difference.
+We can stop increasing the width when `perms[w, 1] > 2,000,000` and similar stop increasing the height when `perms[w, h] > 2,000,000` or `w > h`.
+The second conditions stems from the fact that `perms[w, h] == perms[h, w]` *(it's a mirrored functions)*.
+
+Through these limiting conditions and the fact that each step is pretty fast (just a few additions and multiplications) this algorithm is *really* fast.
+*(We only test around 10000 values before our search space is depleted)*
\ No newline at end of file
diff --git a/www/statics/euler/euler_086.php b/www/statics/euler/euler_086.php
new file mode 100644
index 0000000..e027eb9
--- /dev/null
+++ b/www/statics/euler/euler_086.php
@@ -0,0 +1,19 @@
+ 86,
+ 'title' => 'Cuboid route',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_086_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_086_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_086_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=086',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-086.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 599659030,
+ 'time' => 91822,
+ 'width' => 66,
+ 'height' => 10,
+ 'value' => 1818,
+];
diff --git a/www/statics/euler/euler_086_code.txt b/www/statics/euler/euler_086_code.txt
new file mode 100644
index 0000000..de03a9c
--- /dev/null
+++ b/www/statics/euler/euler_086_code.txt
@@ -0,0 +1,10 @@
+v##### ## > >$30gv >`#v_v
+>"}}@"**50p040p0>1+:v>>1-::*70g:*+v vp01g03_^#-g01:_^#- <: g : :
+ :+ v < >:30p:20 g\/+2/: 30g^* 0>#1v2
+ 71 > >#^ #p #0 2 #<$ v 7gv+:88*%"9"`#^_:88+%:9`#v_:2-#v_v 2 :082g8
+ p2 > > > > # >$>$0>|80/0
+ 0p |!-8_^#-7:_^#-6:_^#-5:_^# -3:< g +p7^<
+ 80 > ^< 0 <^:p010 <^<-! ^10#<
+ > ^ >^ >:55+%:7-!#^_:3-!#^_2-!#^_:3%2-#^_^>^ $g -
+@._^#`g05p04:+g04g08$_^#!: < <>\^
\ No newline at end of file
diff --git a/www/statics/euler/euler_086_description.md b/www/statics/euler/euler_086_description.md
new file mode 100644
index 0000000..0403457
--- /dev/null
+++ b/www/statics/euler/euler_086_description.md
@@ -0,0 +1,17 @@
+A spider, **S**, sits in one corner of a cuboid room, measuring `6 by 5 by 3`,
+and a fly, **F**, sits in the opposite corner.
+By travelling on the surfaces of the room the shortest "straight line"
+distance from **S** to **F** is 10 and the path is shown on the diagram.
+
+
+
+However, there are up to three "shortest" path candidates for any given cuboid and
+the shortest route doesn't always have integer length.
+
+It can be shown that there are exactly `2060` distinct cuboids, ignoring rotations,
+with integer dimensions, up to a maximum size of `M by M by M`,
+for which the shortest route has integer length when `M = 100`.
+This is the least value of M for which the number of solutions first exceeds two thousand;
+the number of solutions when `M = 99` is `1975`.
+
+Find the least value of M such that the number of solutions first exceeds one million.
\ No newline at end of file
diff --git a/www/statics/euler/euler_086_explanation.md b/www/statics/euler/euler_086_explanation.md
new file mode 100644
index 0000000..9d0cad5
--- /dev/null
+++ b/www/statics/euler/euler_086_explanation.md
@@ -0,0 +1,38 @@
+The spider essentially travels on the hypotenuse of a triangle with the sides `A` and `B+C`.
+For it to be the shortest path the condition `A <= B+C` must be true.
+
+The amount of integer-cuboids for a given value M is "All integer-cuboids with `A=M`" plus integer-cuboids(M-1).
+In our loop we start with `M=1` and increment it in every step.
+We also remember the last value (for `M-1`) and loop until the value exceeds one million.
+
+For a given value `A = M` we go through all possible `BC` value (`0 <= BC <= 2*A`) and test if `M^2 + BC^2` is an integer-square.
+If such a number is found and `BC <= A` then this means we have found `BC/2` additional cuboids (there are `BC/2` different `B+C = BC` combinations where `B <= C`)
+If, on the other hand `BC > A` then we have only found `A - (BC + 1)/2 + 1` additional cuboids (because the condition`A <= BC` must be satisfied).
+
+One of the more interesting parts was the `isSquareNumber()` function, which test if a number `x` has an integer square-root.
+To speed this function up *(it takes most of the runtime)* we can eliminate around 12% of the numbers with a few clever tricks.
+For example if the last digit of `x` is `2`, x is never a perfect square-number. Or equally if the last hex-digit is `7`.
+In our program we test twelve conditions like that:
+
+~~~
+x % 16 > 9
+x % 64 > 57
+x % 16 == 2
+x % 16 == 3
+x % 16 == 5
+x % 16 == 6
+x % 16 == 7
+x % 16 == 8
+x % 10 == 2
+x % 10 == 3
+x % 10 == 7
+x % 3 == 2
+~~~
+**Sources:**
+ - [ask-math.com](http://www.ask-math.com/properties-of-square-numbers.html)
+ - [johndcook.com](http://www.johndcook.com/blog/2008/11/17/fast-way-to-test-whether-a-number-is-a-square/)
+ - [stackoverflow.com](http://stackoverflow.com/questions/295579/fastest-way-to-determine-if-an-integers-square-root-is-an-integer)
+
+If none of this pre-conditions is true we have to manually test the number.
+We use the same the same [integer-squareroot](https://en.wikipedia.org/wiki/Integer_square_root) algorithm as in previous problems.
+If `isqrt(x)^2 == x` the we can be sure that x is a perfect square number.
\ No newline at end of file
diff --git a/www/statics/euler/euler_087.php b/www/statics/euler/euler_087.php
new file mode 100644
index 0000000..273e30d
--- /dev/null
+++ b/www/statics/euler/euler_087.php
@@ -0,0 +1,19 @@
+ 87,
+ 'title' => 'Prime power triples',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_087_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_087_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_087_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=087',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-087.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 181436097,
+ 'time' => 27067,
+ 'width' => 1000,
+ 'height' => 1018,
+ 'value' => 1097343,
+];
diff --git a/www/statics/euler/euler_087_code.txt b/www/statics/euler/euler_087_code.txt
new file mode 100644
index 0000000..e4c2993
--- /dev/null
+++ b/www/statics/euler/euler_087_code.txt
@@ -0,0 +1,23 @@
+v000000000
+################################################################
+# ... #
+. . . .
+. . .
+. . . .
+# ... #
+
+>150p0>:50g::+50p\1pv
+ |-">":+1 <
+v $<
+>"}"8* : 8 : 2v>"X"\:10g%\10g/2+p:40 v
+v222p040p03*p01\p0<:vp+2/g01\%g01:p04+1:g<
+>10g%\10g/2+g " "- |>:::50p+>:30g\`!#v_:" "\: v
+|-g03::: +1< ^+g05p+2/ g01\%g01<
+>$$$"o"9*:20p10g*:v^ $<
+vp050p08*9"e"-1p03<
+>:0\:10g%\1 v
+|+1:-1p+3/g0< v+1 ># v# $$< <
+>$"}}P("***90p0>:2g:*60p0>:80g\`!#v_:2g::**60g+:70p90g`#v_0>:80g\`!#^_:2g:*:*70g+:90g`|
+ |-g08:+1$ < #g%\"<"%1g/#v_::"<"/:10g%\10g/3+g\"<"%1g+v
+ ^+1 $<0p05+1g05p+3/g01\%g01:/"<"\ <
\ No newline at end of file
diff --git a/www/statics/euler/euler_087_description.md b/www/statics/euler/euler_087_description.md
new file mode 100644
index 0000000..1548b99
--- /dev/null
+++ b/www/statics/euler/euler_087_description.md
@@ -0,0 +1,12 @@
+The smallest number expressible as the sum of a prime square, prime cube, and prime fourth power is 28.
+In fact, there are exactly four numbers below fifty that can be expressed in such a way:
+
+~~~
+28 = 2^2 + 2^3 + 2^4
+33 = 3^2 + 2^3 + 2^4
+49 = 5^2 + 2^3 + 2^4
+47 = 2^2 + 3^3 + 2^4
+~~~
+
+How many numbers below fifty million can be expressed as the sum of a prime square,
+prime cube, and prime fourth power?
\ No newline at end of file
diff --git a/www/statics/euler/euler_087_explanation.md b/www/statics/euler/euler_087_explanation.md
new file mode 100644
index 0000000..ec64d1d
--- /dev/null
+++ b/www/statics/euler/euler_087_explanation.md
@@ -0,0 +1,11 @@
+Here we iterate quite simply through all the `primes[a]^2 + primes[b]^3 + primes[c]^4` combinations and remember the already found ones.
+
+The prime numbers are generated with the help from our old friend the [Sieve of Eratosthenes](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes)
+*(i improved my befunge snippet for this algorithm a little bit. It's now a bit faster and smaller in size)*.
+
+The main problem was that we needed an bit-array with an size of **fifty million bits**.
+Normally I would simply use an array of size fifty million. But we need to only store Boolean information.
+So I used a "trick" were I stored sixty bits per cell (these are 64-bit values, but I wanted to prevent signed/unsigned problems and I had the problem that the stack is also only 64-bit).
+Unfortunately befunge has no bit operators. So we had to re-invent bit-setting and bit-getting with division, modulo and addition operators.
+
+In the end this didn't make the program fast, but the file size is under 1MB. And I think the run time is acceptable.
\ No newline at end of file
diff --git a/www/statics/euler/euler_088.php b/www/statics/euler/euler_088.php
new file mode 100644
index 0000000..a3e5706
--- /dev/null
+++ b/www/statics/euler/euler_088.php
@@ -0,0 +1,19 @@
+ 88,
+ 'title' => 'Product-sum numbers',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_088_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_088_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_088_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=088',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-088.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 141097978,
+ 'time' => 23852,
+ 'width' => 1024,
+ 'height' => 50,
+ 'value' => 7587457,
+];
diff --git a/www/statics/euler/euler_088_code.txt b/www/statics/euler/euler_088_code.txt
new file mode 100644
index 0000000..34dca05
--- /dev/null
+++ b/www/statics/euler/euler_088_code.txt
@@ -0,0 +1,32 @@
+v XXXX
+ OOOO
+
+### ... ###
+### ... ###
+### ... ###
+
+### ... ###
+### ... ###
+### ... ###
+
+ vp+8+8/g05\%g05:\1:p+3/<
+>"`` "+*20p"}`"*30p8:*:*:*:*40p28*8*8*50p20g>:!#v_1-:40g\:50g%\50g ^
+ vp142p13+1g03p122p+8812 $31g1+31p 082*g::41g\/\1+*4 1p1+082*p051p >41g31g30g21g-+`#v_30g31g41g--1`41g31g`!30g31g4 ^g--:50g%\50g/3+g41g`++3-#^_41g30g31g41g-^
+ ^p+3/g05\ %g05< > 51g:50g%\50g/82*+g:41g\/41p3v
+ vp15+1g15p13+\g13p14*\g14:g+*28/g05\%g05:g1 5p+*28/g05\%g05:g15g+*28/g05\%g05:+1g15p13-\g1<
+ >51g30g1+-#v_ v ^ <
+ v p13+1g13<
+ >51g:50g%\50g/82*+g::1+51g:50g%\50g/82*+p 41g\/41p1+41g*41p51g21g`#v_ ^
+vp310p300 < >51g21p^
+ >3+g61g1+:50g%\50g/3+p61g:50 v >$$v
+ >1pv>71g- #v v# < # $_v#`\g18<
+ 7v0<^:g+3/g< ^ /g05\%g05:g16g+3/g 05\%g05:+1:p16:< >81g-|
+>01-^>::50g%\50^ v_$:0\:50g%\5 0g/3+p^>::50g%\50g/3+g::| $
+ ^_v#-g02:+1<>:71g`#v_81p:>1-:1+ | # ^ $$< 1
+ $ ^ $># 7# 1 p# <$<0 p+3/g05\%g05:\0 +<
+ v00< ^p+3/g05 \%<
+ v+1 <
+ >::91p50g%\50g/3+g+91g:30g-|
+ >$.$@
\ No newline at end of file
diff --git a/www/statics/euler/euler_088_description.md b/www/statics/euler/euler_088_description.md
new file mode 100644
index 0000000..d1f42ef
--- /dev/null
+++ b/www/statics/euler/euler_088_description.md
@@ -0,0 +1,25 @@
+A natural number, N, that can be written as the sum and product of a given set of
+at least two natural numbers, `{a1, a2, ... , ak}` is called a product-sum number:
+`N = a1 + a2 + ... + ak = a1 * a2 * ... * ak`.
+
+For example, 6 = 1 + 2 + 3 = 1 × 2 × 3.
+
+For a given set of size, k, we shall call
+the smallest N with this property a minimal product-sum number.
+The minimal product-sum numbers for sets of size, `k = 2, 3, 4, 5`, and `6` are as follows.
+
+~~~
+k=2: 4 = 2 * 2 = 2 + 2
+k=3: 6 = 1 * 2 * 3 = 1 + 2 + 3
+k=4: 8 = 1 * 1 * 2 * 4 = 1 + 1 + 2 + 4
+k=5: 8 = 1 * 1 * 2 * 2 * 2 = 1 + 1 + 2 + 2 + 2
+k=6: 12 = 1 * 1 * 1 * 1 * 2 * 6 = 1 + 1 + 1 + 1 + 2 + 6
+~~~
+
+Hence for `2<=k<=6`, the sum of all the minimal product-sum numbers is `4+6+8+12 = 30`;
+note that 8 is only counted once in the sum.
+
+In fact, as the complete set of minimal product-sum numbers for `2<=k<=12`
+is `{4, 6, 8, 12, 15, 16}`, the sum is `61`.
+
+What is the sum of all the minimal product-sum numbers for `2<=k<=12000`?
\ No newline at end of file
diff --git a/www/statics/euler/euler_088_explanation.md b/www/statics/euler/euler_088_explanation.md
new file mode 100644
index 0000000..09a55da
--- /dev/null
+++ b/www/statics/euler/euler_088_explanation.md
@@ -0,0 +1,28 @@
+Let's say LIMIT is our maximum value of k (`12 000`).
+
+We start with an array of size LIMIT, filled with ones.
+Our current sum is `LIMIT` and our current product is `1`.
+To kickstart the whole progress we set `arr[1] = 2` (now sum is `LIMIT+1` and product is `2`).
+We also remember the amount of changed fields, which are possible not one (initial `2`).
+
+Now we iterate through all the possible array-combinations (with a few tricks to limit the search-space).
+
+ - In each step we increment array[0]. And update the fields sum and product.
+ This update is not that complex, sum is incrementing by `1` and
+ product is `(product / arr[0]-1) * arr[0]`
+ - While `prod > sum + (LIMIT - len)` we reset the current `arr[pos]` to `arr[pos + 1]`
+ and increment arr[pos + 1]
+ (and obviously increment `pos` and update `sum` and `product`)
+ - After that we have a valid array valud. We can now test for which value of k this is a result
+ (and if is is better than a previous found value)
+ - The value of k is `k := LIMIT - (sum - prod)`
+ The trick here is that we generate a solution by cutting away a lot of the ones at the end of our array
+ to get a solution where `prod = sum` (cutting ones decreemnts sum but leaves prod unchanged).
+ - The condition to cut away only ones is given by our previous condition `prod > sum + (LIMIT - len)`.
+ - After we have gone through all the possible values this way we only have calculate the sum of all the unique values
+
+Because in the last step the list is almost sorted (not totally sorted but there arent that many cases where result[i] > result[i+1])
+we can use a need little algorithm which eliminates duplicates by running through the list
+and doing sum occasional backtracing with an complexity of almost O(N).
+
+I know, the algorithm got a bit complex, but it's pretty fast - even when converted to befunge.
\ No newline at end of file
diff --git a/www/statics/euler/euler_089.php b/www/statics/euler/euler_089.php
new file mode 100644
index 0000000..f86fa0f
--- /dev/null
+++ b/www/statics/euler/euler_089.php
@@ -0,0 +1,19 @@
+ 89,
+ 'title' => 'Roman numerals',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_089_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_089_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_089_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=089',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-089.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 569231,
+ 'time' => 78,
+ 'width' => 73,
+ 'height' => 1009,
+ 'value' => 743,
+];
diff --git a/www/statics/euler/euler_089_code.txt b/www/statics/euler/euler_089_code.txt
new file mode 100644
index 0000000..1d581cb
--- /dev/null
+++ b/www/statics/euler/euler_089_code.txt
@@ -0,0 +1,15 @@
+vABCDEFGHIJKLMNOPQRSTUVWXYZ
+v0123212342
+ ???? ?
+>092p190p5492*+0p55+v
+vp03"d"p0*62"2"p0*83< >::1g"0"-\v
+>"}"4*40p"}"8*94+0p55+^_v#:-1p1 -*\ >42p 22g+22pv
+ >$9:12p>0>:12gg48*-|^10\_^#`\g24::g0-"@"gg21:-1<:
+ >:32p 1-:12gg"@"-0g:42p22p>:|<
+ v+55\g1 +1/+55%"d":\g1+1/"d"%*8"}":\/*8"}":g22$<
+MMMMDCLXXII >%1+1g\ +++32g\-92g+92pv
+MMDCCCLXXXIII |-+9*8"}":p21:+1<
+MMMDLXVIIII >$92g.@
+...
+...
+...
\ No newline at end of file
diff --git a/www/statics/euler/euler_089_description.md b/www/statics/euler/euler_089_description.md
new file mode 100644
index 0000000..beab38c
--- /dev/null
+++ b/www/statics/euler/euler_089_description.md
@@ -0,0 +1,104 @@
+For a number written in Roman numerals to be considered valid there are basic rules which must be followed.
+Even though the rules allow some numbers to be expressed in more than one way there is always a "best" way
+of writing a particular number.
+
+For example, it would appear that there are at least six ways of writing the number sixteen:
+
+~~~
+IIIIIIIIIIIIIIII
+VIIIIIIIIIII
+VVIIIIII
+XIIIIII
+VVVI
+XVI
+~~~
+
+However, according to the rules only XIIIIII and XVI are valid,
+and the last example is considered to be the most efficient, as it uses the least number of numerals.
+
+The 11K text file, roman.txt, contains one thousand numbers written in valid,
+but not necessarily minimal, Roman numerals;
+see **About... Roman Numerals** for the definitive rules for this problem.
+
+Find the number of characters saved by writing each of these in their minimal form.
+
+*Note:* You can assume that all the Roman numerals in the file contain no more
+than four consecutive identical units.
+
+About... Roman Numerals
+=======================
+
+> How do you read and write Roman numerals?
+
+Traditional Roman numerals are made up of the following denominations:
+
+~~~
+I = 1
+V = 5
+X = 10
+L = 50
+C = 100
+D = 500
+M = 1000
+~~~
+
+In order for a number written in Roman numerals to be considered valid there are three basic rules
+which must be followed.
+
+Numerals must be arranged in descending order of size.
+
+`M`, `C`, and `X` cannot be equalled or exceeded by smaller denominations.
+
+`D`, `L`, and `V` can each only appear once.
+
+For example, the number sixteen could be written as `XVI` or `XIIIIII`,
+with the first being the preferred form as it uses the least number of numerals.
+We could not write `IIIIIIIIIIIIIIII` because we are making `X` (ten) from smaller denominations,
+nor could we write VVVI because the second and third rule are being broken.
+
+The "descending size" rule was introduced to allow the use of subtractive combinations.
+For example, four can be written `IV` because it is one before five.
+As the rule requires that the numerals be arranged in order of size it should be clear to
+a reader that the presence of a smaller numeral out of place, so to speak,
+was unambiguously to be subtracted from the following numeral rather than added.
+
+For example, nineteen could be written `XIX` = `X (ten) + IX (nine)`.
+Note also how the rule requires `X` (ten) be placed before `IX` (nine),
+and `IXX` would not be an acceptable configuration (descending size rule).
+Similarly, `XVIV` would be invalid because `V` can only appear once in a number.
+
+Generally the Romans tried to use as few numerals as possible when displaying numbers.
+For this reason, `XIX` would be the preferred form of nineteen over other valid combinations,
+like `XIIIIIIIII` or `XVIIII`.
+
+By mediaeval times it had become standard practice to avoid more than three consecutive
+identical numerals by taking advantage of the more compact subtractive combinations.
+That is, `IV` would be written instead of `IIII`,
+`IX` would be used instead of `IIIIIIIII` or `VIIII`, and so on.
+
+In addition to the three rules given above,
+if subtractive combinations are used then the following four rules must be followed.
+
+ - Only one `I`, `X`, and `C` can be used as the leading numeral in part of a subtractive pair.
+ - `I` can only be placed before `V` and `X`.
+ - `X` can only be placed before `L` and `C`.
+ - `C` can only be placed before `D` and `M`.
+
+Which means that `IL` would be considered to be an invalid way of writing forty-nine,
+and whereas `XXXXIIIIIIIII`, `XXXXVIIII`, `XXXXIX`, `XLIIIIIIIII`, `XLVIIII`, and `XLIX`
+are all quite legitimate, the latter is the preferred (minimal) form.
+However, minimal form was not a rule and there still remain in Rome many examples
+where economy of numerals has not been employed.
+For example, in the famous Colosseum the numerals above the forty-ninth entrance
+is written `XXXXVIIII` rather than `XLIX`.
+
+It is also expected, but not required, that higher denominations should be used whenever possible;
+for example, `V` should be used in place of `IIIII`, `L` should be used in place of `XXXXX`,
+and `D` should be used in place of `CCCCC`.
+However, in the church of Sant'Agnese fuori le Mura (St Agnes' outside the walls),
+found in Rome, the date, `MCCCCCCVI` (1606), is written on the gilded and coffered wooden ceiling;
+I am sure that many would argue that it should have been written `MDCVI`.
+
+So if we believe the adage, "when in Rome do as the Romans do,"
+and we see how the Romans write numerals, then it clearly gives us much more freedom
+than many would care to admit.
\ No newline at end of file
diff --git a/www/statics/euler/euler_089_explanation.md b/www/statics/euler/euler_089_explanation.md
new file mode 100644
index 0000000..96d3b8c
--- /dev/null
+++ b/www/statics/euler/euler_089_explanation.md
@@ -0,0 +1,22 @@
+I don't know why this problem has such a high number.
+
+We simply parse all the roman numbers in the file and create minimal roman literals from them.
+Then we simply sum all the length-differences together.
+
+And it wasn't really hard to write algorithms for these two conversions. Both are pretty straight forward.
+(And for number->roman we didn't even have to go the whole way, we only need the *length* of the result)
+
+For the conversion roman->number we first search for the length of the roman literal.
+Then we go backwards through the letters and get the value of each letter (cached by the array in line one).
+If the value of the letter is greater than the last value we increment the total value (by the letter value),
+otherwise we decrement it.
+I found it easier to traverse the number backwards because we can cache the value of the last digit and do the algorithm this way with less `g` calls.
+
+For the conversion number->optimal_roman_length i found this nice formula:
+
+~~~
+(n/1000) + R[(N%1000)/100] + R[(N%100)/10] + R[N%10]
+
+// n is our number
+// R is defined as an array with { 0, 1, 2, 3, 2, 1, 2, 3, 4, 2 }
+~~~
\ No newline at end of file
diff --git a/www/statics/euler/euler_090.php b/www/statics/euler/euler_090.php
new file mode 100644
index 0000000..b4b84bd
--- /dev/null
+++ b/www/statics/euler/euler_090.php
@@ -0,0 +1,19 @@
+ 90,
+ 'title' => 'Cube digit pairs',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_090_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_090_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_090_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=090',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-090.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 335326352,
+ 'time' => 54366,
+ 'width' => 80,
+ 'height' => 45,
+ 'value' => 1217,
+];
diff --git a/www/statics/euler/euler_090_code.txt b/www/statics/euler/euler_090_code.txt
new file mode 100644
index 0000000..a85eb8a
--- /dev/null
+++ b/www/statics/euler/euler_090_code.txt
@@ -0,0 +1,45 @@
+v X_XXOO ######### v6$< > #g #0 #+ #8 #: #:v#<>v
+2 X ##########v 2+4\1p22+g22!g2+4:< _^#-9:%+55*:p1+4\1p12+g12!g1+4:/+55*::_v 1g
+9 X ##########v1+4\1p12+g12!g1+4:< _v#-9:%+55*:p2+4\1p22+g22!g2+4:/+55*::< 26
+3 C >p #^6$ #< #v ># #< 1-:|$`
+*>020p8>:0\9+0p:#v_$021p022p9>:0\4+1p:0\4+2p:#v_$55+^vg0+9p0+9\!g0+9::::< >^2
++p ^-1 <^00 <^-1 < v$$_!#v_1- # #v #! #+^#`6g2<
+33 ^ < >$ ^ v_8 ^
+>^ @.g02< >:1-\#v_$ > 8^
+ >:0\4+1p >:1-\#v_$ v |g1+4:<9_v#-g12 6<
+ vp1+4\1:<|g1+4:<9_v#-g125p1+4\1:< 2> ^
+ ^0 ^< >#1>:0\4+1p >:1-\#^_$ ^
+ $# ^ $$ < #$
+ >#^_1- :!#^_1- :!#^_@
+ ! > > >22g6- #v _v
+ >v ^: ^# < >:1-\#v_$ #2v
+ p >:0\4+2p >:1-\#v_$ v |g2+4:<9<< > v
+ 2 vp2+4\1:<|g2+4:<9_v#-g225p2+4\1:< v < >g1+20pv
+ + ^0 ^< >#1>:0\4+2p # >:1-\#^_$ ^ ^02p+g<
+ 9 $# ^ #$$ < ^ $< $# >%\"P"/33^
+>#4> :!#^_1- :!#^_1- :!#^_@^"P":\g03<
+ 0 v+64p04+g1+94!g1+64< ># #< #v# #< v #
+ p >2g!49+2g+50pv>40g50g+#^_046+1p149+1p046+2p149+2pv>146+1p049+1p146+2p 049vv<
+^<^2+641< v0p2+9$0 41p2+640_v#!g05v v $# $# # < > ^
+> 1+:!#^_1- :!#^_1- #^ #< :!#^_1-:!#^_@>33g+g:30g-#v_$$^ <
+ ^ -# < 9 ^ < >57*- !| #
+ > >060p070p9v< 9p070p060< < ^/"P"\%"P"::< v <
+ v*2g06g1+4:< $v < >\v^-1<*" ("<#
+ >+60p:1-\ #^_^>:4+2g70g2*+70p:1-\#^_$70g60g:70g`#^_>48*:**+30p^
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
+################################################################################
\ No newline at end of file
diff --git a/www/statics/euler/euler_090_description.md b/www/statics/euler/euler_090_description.md
new file mode 100644
index 0000000..e33db9b
--- /dev/null
+++ b/www/statics/euler/euler_090_description.md
@@ -0,0 +1,36 @@
+Each of the six faces on a cube has a different digit (0 to 9) written on it;
+the same is done to a second cube.
+By placing the two cubes side-by-side in different positions we can form a variety of 2-digit numbers.
+
+For example, the square number 64 could be formed:
+
+~~~
+ +-------+ +-------+
+ / /| / /|
++-------+ | +-------+ |
+| | | | | |
+| 6 | + | 4 | +
+| |/ | |/
++-------+ +-------+
+~~~
+
+In fact, by carefully choosing the digits on both cubes it is possible to display
+all of the square numbers below one-hundred: `01`, `04`, `09`, `16`, `25`, `36`, `49`, `64`, and `81`.
+
+For example, one way this can be achieved is by placing `{0, 5, 6, 7, 8, 9}` on one cube
+and `{1, 2, 3, 4, 8, 9}` on the other cube.
+
+However, for this problem we shall allow the `6` or `9` to be turned upside-down
+so that an arrangement like `{0, 5, 6, 7, 8, 9}` and `{1, 2, 3, 4, 6, 7}` allows
+for all nine square numbers to be displayed; otherwise it would be impossible to obtain `09`.
+
+In determining a distinct arrangement we are interested in the digits on each cube, not the order.
+
+ - `{1, 2, 3, 4, 5, 6}` is equivalent to `{3, 6, 4, 1, 2, 5}`
+ - `{1, 2, 3, 4, 5, 6}` is distinct from `{1, 2, 3, 4, 5, 9}`
+
+But because we are allowing `6` and `9` to be reversed, the two distinct sets in
+the last example both represent the extended set `{1, 2, 3, 4, 5, 6, 9}` for the
+purpose of forming 2-digit numbers.
+
+How many distinct arrangements of the two cubes allow for all of the square numbers to be displayed?
\ No newline at end of file
diff --git a/www/statics/euler/euler_090_explanation.md b/www/statics/euler/euler_090_explanation.md
new file mode 100644
index 0000000..a578c7e
--- /dev/null
+++ b/www/statics/euler/euler_090_explanation.md
@@ -0,0 +1,35 @@
+We have nine square numbers that need to be represented.
+For each number we can either use dice one for the first digit and dice two for the second or the other way around. Together there are `2^9 (=512)` possibilities.
+In our program we iterate through them all (a simple binary counter at program position [9,0]).
+
+In each turn we remember which numbers would need to be written on the first dice and which on the second one (we have two boolean arrays at [4,1] and [4,2]). If one dice needs more than six numbers on it we can directly throw this combination away and go on with the next number in our binary counter.
+
+It's important that in this phase we have no nines. Every nine is replaced with a six (so we use `3*3 = 09` and `7*7 = 46`) The nines are later taken into account.
+
+Now most of the time one or both dices have less than six digits on it (sometimes even only four).
+We iterate now through all possible combinations of six digits with our found set as a basis. (So if one dice has 5 digits and the other one 4 we generate an additional 150 combinations (`5*5*6`).
+
+Then in the last step we look at each dice and see if it contains a six and no nine. If this is the case we generate another combination where the six and the nine is exchanged. (Because we do this for each dice individually we can for each given combination possibly generate four new ones *(original, D1 exchanged, D2 exchanged, both exchanged)*).
+
+Now we have every possible combinations that fits our initial condition. To weed out all the duplicates we generate a hash from the combination and remember previously found values in an 80x16 big hashmap (originally I had the map way bigger, but after my first successful run I could shrink the size to a more fitting value).
+
+The hash is simply the binary representation of **D1** and **D2** concatenated (one for "has this digit", zero for "does not have this digit").
+Because the order of the dices is irrelevant in our result we ignore it also in our hash and always use the dice with the smaller hash value as the lower bits of the total hash (this way `HASH(D1,D2) == HASH(D2,D1)`).
+
+One problem of writing this program (except the metric fuck-ton of code all this needs, seriously I filled a 80x30 grid only with logic, there is more raw code than space for the 1280-elements hashmap) were the filling methods.
+
+In my C# test program I had three functions:
+
+ - **PadLeft** fills the left digit up to six digits with all possible values
+ - **PadRight** fills the right digit up to six digits with all possible values
+ - **PadNine** exchanges `6` with `9` in the left and right digit to generate all possible combinations
+ - **Output** Test if a is already in the hashmap, if not increments the counter
+
+Now the function PadLeft() calls PadRight() which calls PadNine(), which calls Output(). Each at three to four different places.
+So in my befunge program I needed to do the same thing every sane procedural language does:
+Remember the back jump address, so after PadNine() is called we know where in PadRight() we have to continue the program flow.
+
+Unfortunately this is in befunge not really good to write and leads to a lot of boilerplate code, but it's still better than writing the Output function twenty-seven times in different places.
+
+A last note: This is the first program where I put the big data structures below the actual code. It's nice to have all the program logic at the top of the file, but every time I address something down there the constants for the Y value take more space. This is also the reason my variables are always in the top left corner, there I can address them with only three commands (`xyg` bzw `xyp`) as long as `x` and `y` are below ten.
+So I think it's not too bad to have the data below the code but for the future I will keep my old organization.
\ No newline at end of file
diff --git a/www/statics/euler/euler_091.php b/www/statics/euler/euler_091.php
new file mode 100644
index 0000000..ec728dd
--- /dev/null
+++ b/www/statics/euler/euler_091.php
@@ -0,0 +1,19 @@
+ 91,
+ 'title' => 'Right triangles with integer coordinates',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_091_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_091_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_091_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=091',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-091.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 3072923,
+ 'time' => 343,
+ 'width' => 36,
+ 'height' => 5,
+ 'value' => 14234,
+];
diff --git a/www/statics/euler/euler_091_code.txt b/www/statics/euler/euler_091_code.txt
new file mode 100644
index 0000000..7f938bb
--- /dev/null
+++ b/www/statics/euler/euler_091_code.txt
@@ -0,0 +1,5 @@
+"2":11p031p41p>11g51p51g1> #1 #g #$41p#^_31g311g:**+.@>$p v1+
+>1g51g:61g-\*41g%!2*+31p61g1+61pv!56
+^ >51g#^ #:1# - #1:#g5#11#4 ^# _^1
+^3_^#! +`g11g16`*:g14*-\g16:g15< p<
\ No newline at end of file
diff --git a/www/statics/euler/euler_091_description.md b/www/statics/euler/euler_091_description.md
new file mode 100644
index 0000000..b807097
--- /dev/null
+++ b/www/statics/euler/euler_091_description.md
@@ -0,0 +1,15 @@
+The points `P(x1, y1)` and `Q(x2, y2)` are plotted at integer co-ordinates and are joined to the origin,
+`O(0,0)`, to form `OPQ`.
+
+
+
+There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate
+lies between 0 and 2 inclusive; that is,
+
+~~~
+0 <= x1, y1, x2, y2 <= 2.
+~~~
+
+
+
+Given that `0 <= x1, y1, x2, y2 <= 50`, how many right triangles can be formed?
\ No newline at end of file
diff --git a/www/statics/euler/euler_091_explanation.md b/www/statics/euler/euler_091_explanation.md
new file mode 100644
index 0000000..85bdecd
--- /dev/null
+++ b/www/statics/euler/euler_091_explanation.md
@@ -0,0 +1,102 @@
+This was mostly a mathematical problem.
+
+Lets go step by step through my solution:
+
+We have a triangle with three corners, `O(o_x, o_y)`, `Q(q_x, q_y)` and `P(p_x, p_y)`, where `O = (0,0)`.
+We can quickly see that there are three types of solutions, triangles where O has the right angle,
+triangles where Q has the right angle and triangles where P has the right angle.
+
+The amount of triangles in group two (angle at Q) and group three (angle at P) are identical (!)
+Because for every triangle in group two there is a triangle in group three which has the points P and Q mirrored at the vertical Axis `(1, 1)`.
+So when we have a triangle `O(0, 0); Q1(q1_x, q1_y); P(p1_x, p1_y)` the corresponding mirrored triangle is
+~~~
+q2_x = q1_y
+q2_y = q1_x
+p2_x = p1_y
+p2_y = p1_x
+~~~
+
+These two groups (two and three) are also mutually exclusive, because if `Q1 == P2` and `Q2 == P1` then the vectors `OP` and `OQ` would have equal length and
+the only possible right angle could be at point O (and not at P or Q).
+
+Now that we have proven that `count(group_2) == count(group_3)` we only have to find that triangle count and the amount of triangles in group one.
+
+First group one:
+
+To have an right angle at the zero point `O(0, 0)` both other points have to lie on an axis.
+We say point Q lies on the x-axis and point P on the Y-axis. All combinations lead to valid and unique triangles, the only disallowed point is the origin `(0, 0)`.
+So we have `SIZE` possible positions on the x-axis and `SIZE` possible positions on the y-axis. This leads to `SIZE * SIZE` different unique triangles:
+
+~~~
+count(group_1) = SIZE * SIZE
+~~~
+
+Now group 2/3
+
+Because we need to define a bit of semantics we say our point Q is the lower-right point of the triangle (and P is the upper left),
+similar to the project-euler example image. Also we want our right angle to be at point Q (between the vectors OP and PQ).
+First we can look at the trivial triangles, the ones where Q lies on the x-axis and P has the same x-coordinate as Q.
+These triangles all have an right angle at Q and are valid solutions. And because there are `SIZE` possible positions for Q (all x-axis positions except `(0,0)`)
+and for each of these there are `SIZE` possible positions for P (all points on the same x-value as Q, except `y = 0`)
+there are `SIZE*SIZE` trivial triangles with an right angle at Q.
+
+~~~
+count(group_2_triv) = count(group_3_triv) = SIZE * SIZE
+~~~
+
+For the remaining triangle we can finally - kind of - start programming.
+We go through all remaining points (q_x, q_y) where `q_x > 0 && q_y > 0` (because the axis are already covered by our trivial cases).
+
+For every point (that we assume is Q) we calculate the vector OQ:
+
+~~~
+oq_x = q_x - 0 // trivial, yeah i know. In the final program this is all optimized away
+oq_y = q_y - 0
+~~~
+
+And we calculate the direction of the vector QP (under the assumption that Q has a right angle and thus OQ and QP form a right angle).
+This is simply the vector OQ rotate by 90° CW:
+
+~~~
+v_qp_x = -oq_y;
+v_qp_y = oq_x;
+~~~
+
+Now we search for integer solutions of `P = Q + n * v_QP`. Each solution, that also falls in our SIZE bounds is a valid triangle.
+To find these we go through all the possible y locations out point P can have.
+It is not possible that one p_y value responds to multiple p_x values, because then QP would be horizontal
+and these triangles are already acknowledged in our trivial cases of group_2 / group_3.
+
+So for each (possibly valid) p_y value we can calculate the corresponding p_x value:
+
+~~~
+p_y = q_y + n * v_qp_y
+n = (p_y - q_y) / v_qp_y
+
+p_x = q_x + n * v_qp_x
+ = q_x + ((p_y - q_y) / v_qp_y) * v_qp_x
+ = q_x + ((p_y - q_y) * v_qp_x / v_qp_y)
+~~~
+
+First we want to test if `(p_y - q_y) * v_qp_x` is a multiple of `v_qp_y`.
+If this were not the case than p_x is not an integer and this is not an integer solution
+(then we would simply continue with the next y value until y > SIZE and we have reached our limit).
+But if P(p_x, p_y) **has** two integer components we only need to test if p_x is greater than zero
+(because otherwise the triangle would be out of our defined bounds) and then we can increment out triangle counter.
+Be aware that we have in this step practically found two unique triangles, this one and its mirrored counter part (see explanation at the beginning).
+Now we continue our looping, first until we have tested all possible p_y values (until p_y grows greater than our bounds, SIZE)
+and then until we have tested all valid points for Q.
+
+In the end we only have to add our values together and we have our result:
+
+~~~
+result = c_group_1 + 2 * c_group_23
+
+c_group_23 = c_group_23_triv + c_group_23_nontriv
+~~~
+
+This is one of the problems that translate **really** well into befunge, because there are no big data structures and not even a lot of calculations.
+Most of the work is done before we start to write code and the challenge is finding the correct approach.
+
+*After note:* I really want a price or something for the compression of this program.
+Everything is crunched into a 36x5 rectangle and there are nearly no unused codepoints...
\ No newline at end of file
diff --git a/www/statics/euler/euler_092.php b/www/statics/euler/euler_092.php
new file mode 100644
index 0000000..39e81cc
--- /dev/null
+++ b/www/statics/euler/euler_092.php
@@ -0,0 +1,19 @@
+ 92,
+ 'title' => 'Square digit chains',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_092_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_092_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_092_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=092',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-092.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 2959813630,
+ 'time' => 379925,
+ 'width' => 80,
+ 'height' => 16,
+ 'value' => 8581146,
+];
diff --git a/www/statics/euler/euler_092_code.txt b/www/statics/euler/euler_092_code.txt
new file mode 100644
index 0000000..8cbfb5c
--- /dev/null
+++ b/www/statics/euler/euler_092_code.txt
@@ -0,0 +1,16 @@
+v $$ T # #######################################################################
+ # #######################################################################
+ XX # #######################################################################
+ # #######################################################################
+ # #######################################################################
+ # #######################################################################
+ # #######################################################################
+ # #######################################################################
+
+ v p1*93"Y" p0+551 $<
+> "G"8*:32p"}2(("***22p020p030p >1-:0\:"G"%9+\"G"/p:!|
+ v pp02+1:g027:$<^ ># v# <
+ >22g:>:32g`#v_::"G"%9+\"G"/g:!#^_:1-!#v_ :"Y"-| # >1-:20p7\g50g\: v
+ >0\>:55+%:*\ :#v_$$11v >30g1+30p>50p$20g:|:g02p/"G"\+9%"G"<
+ >3 v^/+55g05+p05< >$@ v1 ::-1$<
+ ^_^# _^#># 0# g# .# $# ^# <*0 <
\ No newline at end of file
diff --git a/www/statics/euler/euler_092_description.md b/www/statics/euler/euler_092_description.md
new file mode 100644
index 0000000..6dde08d
--- /dev/null
+++ b/www/statics/euler/euler_092_description.md
@@ -0,0 +1,12 @@
+A number chain is created by continuously adding the square of the digits in a number to
+form a new number until it has been seen before.
+
+For example,
+
+44 ? 32 ? 13 ? 10 ? 1 ? 1
+85 ? 89 ? 145 ? 42 ? 20 ? 4 ? 16 ? 37 ? 58 ? 89
+
+Therefore any chain that arrives at 1 or 89 will become stuck in an endless loop.
+What is most amazing is that EVERY starting number will eventually arrive at 1 or 89.
+
+How many starting numbers below ten million will arrive at 89?
\ No newline at end of file
diff --git a/www/statics/euler/euler_092_explanation.md b/www/statics/euler/euler_092_explanation.md
new file mode 100644
index 0000000..faadef5
--- /dev/null
+++ b/www/statics/euler/euler_092_explanation.md
@@ -0,0 +1,13 @@
+My approach to this problem is pretty crude. Perhaps I will later come back and try to find a better algorithm.
+Currently we iterate (brute-force) through all possible numbers and count the chains that end with one.
+The `next()` function is implemented like this:
+
+~~~~~~~~~~~~~~~~~~~
+0\>:55+%:*\ :#v_$$
+ ^/+55g05+p05<
+~~~~~~~~~~~~~~~~~~~
+
+We also remember in an 8x71 cache all previously found numbers so we can abort some sequences before we reach `1` or `89`.
+This is the main optimization from pure brute-force in this program.
+
+We can prove that an 568-element cache is enough because no number in the sequence (except the first) can be greater than `9^2 * 7` (` = 567`)
\ No newline at end of file
diff --git a/www/statics/euler/euler_093.php b/www/statics/euler/euler_093.php
new file mode 100644
index 0000000..7b747a0
--- /dev/null
+++ b/www/statics/euler/euler_093.php
@@ -0,0 +1,19 @@
+ 93,
+ 'title' => 'Arithmetic expressions',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_093_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_093_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_093_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=093',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-093.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 305514916,
+ 'time' => 42167,
+ 'width' => 111,
+ 'height' => 211,
+ 'value' => 1258,
+];
diff --git a/www/statics/euler/euler_093_code.txt b/www/statics/euler/euler_093_code.txt
new file mode 100644
index 0000000..369da91
--- /dev/null
+++ b/www/statics/euler/euler_093_code.txt
@@ -0,0 +1,138 @@
+v XXXX ####################################################################################################
+ XX ####################################################################################################
+ ####################################################################################################
+ C ####################################################################################################
+ OOOO ####################################################################################################
+ ####################################################################################################
+ OOOO O ####################################################################################################
+ OOOO O ####################################################################################################
+ OOOO O ####################################################################################################
+ OOOO O ####################################################################################################
+ ################ ... ... ... ... ################
+0 ####################################################################################################
+2 ####################################################################################################
+1 ####################################################################################################
+p ####################################################################################################
+" ####################################################################################################
+H ####################################################################################################
+# ####################################################################################################
+" ####################################################################################################
+* ####################################################################################################
+2 ####################################################################################################
+3 ####################################################################################################
+p ####################################################################################################
+0 ####################################################################################################
+3 ####################################################################################################
+1 ####################################################################################################
+p ####################################################################################################
+
+>"}P"*>1-:" "\:"d"v
+ |:p/"d"\+9% <
+v $< >4g.24g.34g.44g.@
+>120p>20g1+30p >30g1+40p >40g1+50p > "X" 20g55+*30g+50g55+*40v
+ |-7p02:+1g02<|-8p03:+1g03<|-9p04:+1g04<|-5-5p05:+1g05p13+1g13p+g <
+v < # ^< ^< ^<
+> 31g1-!#^_21g1+21p031p>120p>20g1+30p >30g1+40p >40g1+50p >20g55+*30g+50g55+*40g+g"X"-v
+ |-7p02:+1g02<|-8p03:+1g03<|-9p04:+1g04<|-5-5p05:+1g05< _v
+^ < ^< ^< ^< >^
+ vp670p64*g32g05p63*g32g04p62*g32g03p61*g32g02 ># ^# <
+ v 76g:1+76pv >77g:1+77pv >78g:1+78pv ^
+> #v #: #< #v #: #< ^ v: <
+ v-1_$077p16g26g+17p36g27p46g37p ^v-1_$078p17g27g+18p37g28p ^v-1_$18g28g+19p v
+ >: v >: v >: v
+ v-1_$077p16g36g+17p26g27p46g37p ^v-1_$078p17g37g+18p27g28p ^v-1_$18g28g-19p v
+ >: v >: v >: v
+ v-1_$077p16g46g+17p26g27p36g37p ^v-1_$078p37g18p27g17g+28p ^v-1_$28g18g-19p v
+ >: v >: v >: v
+ v-1_$077p46g17p26g16g+27p36g37p ^v-1_$078p17g18p27g37g+28p ^v-1_$18g28g*23g/19p v
+ >: v >: v >: v
+ v-1_$077p16g17p26g36g+27p46g37p ^v-1_$078p27g18p37g17g+28p ^v-1_$28g!#v_18g23g*28g/19p v
+ >: v >: v >: v > ^
+ v-1_$077p16g17p26g46g+27p36g37p ^v-1_$078p17g18p37g27g+28p ^v $_$18g!#v_28g23g*18g/19p v
+ >: v >: v ^ < > ^
+ v-1_$077p46g17p26g27p36g16g+37p ^v-1_$078p17g27g-18p37g28p ^ <
+ >: v >: v |+!!%g32g91!!-g12/g32g91<
+ v-1_$077p16g17p46g27p36g26g+37p ^v-1_$078p17g37g-18p27g28p ^ 3
+ >: v >: v 1
+ v-1_$077p16g17p26g27p36g46g+37p ^v-1_$078p37g18p27g17g-28p ^ g
+ >: v >: v 1
+ v-1_$077p36g17p26g27p46g16g+37p ^v-1_$078p17g18p27g37g-28p ^ +
+ >: v >: v 3
+ v-1_$077p16g17p36g27p46g26g+37p ^v-1_$078p27g18p37g17g-28p ^ 1
+ >: v >: v p
+ v-1_$077p16g17p26g27p46g36g+37p ^v-1_$078p17g18p37g27g-28p ^ 2
+ >: v >: v 0
+ v-1_$077p16g26g-17p36g27p46g37p ^v-1_$078p17g27g*23g/18p37g28p ^ g
+ >: v >: v 1
+ v-1_$077p16g36g-17p26g27p46g37p ^v-1_$078p17g37g*23g/18p27g28p ^ 4
+ >: v >: v p
+ v-1_$077p16g46g-17p26g27p36g37p ^v-1_$078p37g18p27g17g*23g/28p ^ 3
+ >: v >: v 0
+ v-1_$077p46g17p26g16g-27p36g37p ^v-1_$078p17g18p27g37g*23g/28p ^ g
+ >: v >: v 2
+ v-1_$077p16g17p26g36g-27p46g37p ^v-1_$078p27g18p37g17g*23g/28p ^ 4
+ >: v >: v p p
+ v-1_$077p16g17p26g46g-27p36g37p ^v-1_$078p17g18p37g27g*23g/28p ^ 4
+ >: v >: v ^44g05p4 3g0<
+ v-1_$077p46g17p26g27p36g16g-37p ^v-1_$27g!#v_078p17g23g*27g/18p37g28p ^
+ >: v >: v > ^
+ v-1_$077p16g17p46g27p36g26g-37p ^v-1_$27g!#v_078p17g23g*37g/18p27g28p ^
+ >: v >: v > ^
+ v-1_$077p16g17p26g27p36g46g-37p ^v-1_$27g!#v_078p37g18p27g23g*17g/28p ^
+ >: v >: v > ^
+ v-1_$077p36g17p26g27p46g16g-37p ^v-1_$27g!#v_078p17g18p27g23g*37g/28p ^
+ >: v >: v > ^
+ v-1_$077p16g17p36g27p46g26g-37p ^v-1_$27g!#v_078p27g18p37g23g*17g/28p ^
+ >: v >: v > ^
+ v-1_$077p16g17p26g27p46g36g-37p ^v $_$27g!#v_078p17g18p37g23g*27g/28p ^
+ >: v ^ < > ^
+ v-1_$077p16g26g*23g/17p36g27p46g37p ^
+ >: v
+ v-1_$077p16g36g*23g/17p26g27p46g37p ^
+ >: v
+ v-1_$077p16g46g*23g/17p26g27p36g37p ^
+ >: v
+ v-1_$077p46g17p26g16g*23g/27p36g37p ^
+ >: v
+ v-1_$077p16g17p26g36g*23g/27p46g37p ^
+ >: v
+ v-1_$077p16g17p26g46g*23g/27p36g37p ^
+ >: v
+ v-1_$077p46g17p26g27p36g16g*23g/37p ^
+ >: v
+ v-1_$077p16g17p46g27p36g26g*23g/37p ^
+ >: v
+ v-1_$077p16g17p26g27p36g46g*23g/37p ^
+ >: v
+ v-1_$077p36g17p26g27p46g16g*23g/37p ^
+ >: v
+ v-1_$077p16g17p36g27p46g26g*23g/37p ^
+ >: v
+ v-1_$077p16g17p26g27p46g36g*23g/37p ^
+ >: v
+ v-1_$26g!#v_077p16g23g*26g/17p36g27p46g37p ^
+ >: v > ^
+ v-1_$36g!#v_077p16g23g*36g/17p26g27p46g37p ^
+ >: v > ^
+ v-1_$46g!#v_077p16g23g*46g/17p26g27p36g37p ^
+ >: v > ^
+ v-1_$16g!#v_077p46g17p26g23g*16g/27p36g37p ^
+ >: v > ^
+ v-1_$36g!#v_077p16g17p26g23g*36g/27p46g37p ^
+ >: v > ^
+ v-1_$46g!#v_077p16g17p26g23g*46g/27p36g37p ^
+ >: v > ^
+ v-1_$16g!#v_077p46g17p26g27p36g23g*16g/37p ^
+ >: v > ^
+ v-1_$26g!#v_077p16g17p46g27p36g23g*26g/37p ^
+ >: v > ^
+ v-1_$46g!#v_077p16g17p26g27p36g23g*46g/37p ^
+ >: v > ^
+ v-1_$16g!#v_077p36g17p26g27p46g23g*16g/37p ^
+ >: v > ^
+ v-1_$26g!#v_077p16g17p36g27p46g23g*26g/37p ^
+ >: v > ^
+ v $_$36g!#v_077p16g17p26g27p46g23g*36g/37p ^
+^ ># #< ^
+ >" "20g55+*30g+50g55+*40g+p^
\ No newline at end of file
diff --git a/www/statics/euler/euler_093_description.md b/www/statics/euler/euler_093_description.md
new file mode 100644
index 0000000..8b10f28
--- /dev/null
+++ b/www/statics/euler/euler_093_description.md
@@ -0,0 +1,22 @@
+By using each of the digits from the set, `{1, 2, 3, 4}`, exactly once,
+and making use of the four arithmetic operations (`+`, `?`, `*`, `/`) and brackets/parentheses,
+it is possible to form different positive integer targets.
+
+For example,
+
+~~~
+8 = (4 * (1 + 3)) / 2
+14 = 4 * (3 + 1 / 2)
+19 = 4 * (2 + 3) ? 1
+36 = 3 * 4 * (2 + 1)
+~~~
+
+Note that concatenations of the digits, like `12 + 34`, are not allowed.
+
+Using the set, {1, 2, 3, 4}, it is possible to obtain thirty-one different target numbers
+of which 36 is the maximum, and each of the numbers 1 to 28 can be obtained
+before encountering the first non-expressible number.
+
+Find the set of four distinct digits, `a < b < c < d`, for which the
+longest set of consecutive positive integers, 1 to n, can be obtained,
+giving your answer as a string: abcd.
\ No newline at end of file
diff --git a/www/statics/euler/euler_093_explanation.md b/www/statics/euler/euler_093_explanation.md
new file mode 100644
index 0000000..e745f88
--- /dev/null
+++ b/www/statics/euler/euler_093_explanation.md
@@ -0,0 +1,73 @@
+This one needs a little bit of a bigger explanation:
+
+First let me say that I'm aware that this is neither the fastest algorithm nor the best algorithm to represent in funge-space. But its reasonable fast and I liked the challenge of doing such a big program (in terms of raw code size) in befunge.
+
+First we take a 4-dimensional cache of all possible number combinations (so an `bool[10][10][10][10]` array) where we remember if a combination is valid.
+In our program we represent it as an 2D-field with `X=s1*10+s2` and `Y=s4*10+s3`.
+
+Initially we set all fields to true where `0 n*C = n*A + n*B
+~~~
+
+A little more attention is needed when doint multiplication and division, for the first we have to divide by the factor after the operation and for the second we have to multiply it:
+
+~~~
+C = A*B => n*C = (n*A * n*B) / n
+C = A/B => n*C = ((n*A)*n / (n*B)
+~~~
+
+It is important that we multiply the dividend by the factor and not the result of the division, otherwise the decimal places will get lost.
+
+As usual a final note from me: Nice problem. 10/10 would solve again
\ No newline at end of file
diff --git a/www/statics/euler/euler_094.php b/www/statics/euler/euler_094.php
new file mode 100644
index 0000000..be857b1
--- /dev/null
+++ b/www/statics/euler/euler_094.php
@@ -0,0 +1,19 @@
+ 94,
+ 'title' => 'Almost equilateral triangles',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_094_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_094_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_094_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=094',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-094.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 2009,
+ 'time' => 0,
+ 'width' => 40,
+ 'height' => 5,
+ 'value' => 518408346,
+];
diff --git a/www/statics/euler/euler_094_code.txt b/www/statics/euler/euler_094_code.txt
new file mode 100644
index 0000000..3535e9c
--- /dev/null
+++ b/www/statics/euler/euler_094_code.txt
@@ -0,0 +1,5 @@
+"}}2( "****04003pp201p102p>04g01g2*`#v_v
+Xv2*2g10**!%3*g20-2g10!-1%3*g102`2g10< 0
+X>-*03g+03p01g2*3%2-!01g2+# 02g*3%v 3
+Xv*2g10+*2g20g10p30+g30*+* g1022*!< @.g<
+C>02g3*+01p02p ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_094_description.md b/www/statics/euler/euler_094_description.md
new file mode 100644
index 0000000..bca5aee
--- /dev/null
+++ b/www/statics/euler/euler_094_description.md
@@ -0,0 +1,8 @@
+It is easily proved that no equilateral triangle exists with integral length sides and integral area.
+However, the almost equilateral triangle 5-5-6 has an area of 12 square units.
+
+We shall define an almost equilateral triangle to be a triangle
+for which two sides are equal and the third differs by no more than one unit.
+
+Find the sum of the perimeters of all almost equilateral triangles with integral side lengths
+and area and whose perimeters do not exceed one billion (1,000,000,000).
\ No newline at end of file
diff --git a/www/statics/euler/euler_094_explanation.md b/www/statics/euler/euler_094_explanation.md
new file mode 100644
index 0000000..5d5dfac
--- /dev/null
+++ b/www/statics/euler/euler_094_explanation.md
@@ -0,0 +1,8 @@
+Nothing much to say about this one, we play a bit with the triangle formulas until we reach something that looks like a [Pell equation](https://en.wikipedia.org/wiki/Pell%27s_equation).
+My approach is basically the same as the one on [mathblog.dk](http://www.mathblog.dk/project-euler-94-almost-equilateral-triangles/), but he explains it better.
+(And I improved my approach a bit after I read his article, his math skills are pretty good :D).
+
+The code is in a way interesting because it only has a single conditional operator.
+I could remove two conditional by multiplying the increment with the normalized condition (`0`|`1`).
+This way `if (condition) { x += increment; }` becomes ` x += (int)(condition) * increment`,
+which is a neat way to safe a bit of space in our program (and the resulting 40x5 code is pretty compact)
\ No newline at end of file
diff --git a/www/statics/euler/euler_095.php b/www/statics/euler/euler_095.php
new file mode 100644
index 0000000..1aed909
--- /dev/null
+++ b/www/statics/euler/euler_095.php
@@ -0,0 +1,19 @@
+ 95,
+ 'title' => 'Amicable chains',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_095_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_095_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_095_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=095',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-095.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 1053466251,
+ 'time' => 242737,
+ 'width' => 2017,
+ 'height' => 1035,
+ 'value' => 14316,
+];
diff --git a/www/statics/euler/euler_095_code.txt b/www/statics/euler/euler_095_code.txt
new file mode 100644
index 0000000..4da5073
--- /dev/null
+++ b/www/statics/euler/euler_095_code.txt
@@ -0,0 +1,23 @@
+v # ## .... ## ## .... ##
+ X # ## ## ## ##
+ XXX #
+ XX # . . . .
+ X # . . . .
+ X # . . . .
+ # . . . .
+ #
+ # ## .... ## ## .... ##
+ CCC # ## ## ## ##
+
+>"}"8*19p"q"9*29p"}}@"**39p012p014p39g15p39g>1-:0\:19g/9+\19g%p v
+v < |:p%g91\+g92/g91:\0:<
+1 v+1p%g91\+g92 /g91:\+g31g%g91\+g92/g91 ::<
+>:13p2>:13g*:39g\`#^ #$ #< |
+^_$# 6# v# -g93:+1$$< vp51g\7:<
+v < >v>g+\19g%g22pv >v >v >v > v
+> :23p :19g/9+\19g%g!|> 23g:70p11v >22g:0`|>:39g\`|>:23g-|$ >:7\g22g-| # > 32g14p:7\g15pv
+| -g93:+1 g32 < $< < <0 ^ < >131p:12g\-32p32g14g`||*g13`\g51g\7:<
+>$15g.@ ^92/g91:p2< ^p22g%g< >31p032p0^ < v
+ >9g%p22g:19g/29g+\19^ v< |-g21:+1 < <
+ ^ < <|g13$< <
+ ^1\+9/g91:\1pp21+1:g217:g22<_^#!g%g91\+9/g91:g22<
\ No newline at end of file
diff --git a/www/statics/euler/euler_095_description.md b/www/statics/euler/euler_095_description.md
new file mode 100644
index 0000000..09d2721
--- /dev/null
+++ b/www/statics/euler/euler_095_description.md
@@ -0,0 +1,18 @@
+The proper divisors of a number are all the divisors excluding the number itself.
+For example, the proper divisors of 28 are 1, 2, 4, 7, and 14.
+As the sum of these divisors is equal to 28, we call it a perfect number.
+
+Interestingly the sum of the proper divisors of 220 is 284 and the sum of the
+proper divisors of 284 is 220, forming a chain of two numbers.
+For this reason, 220 and 284 are called an amicable pair.
+
+Perhaps less well known are longer chains.
+For example, starting with 12496, we form a chain of five numbers:
+
+~~~
+12496 -> r -> 15472 -> 14536 -> 14264 (-> 12496 -> ...)
+~~~
+
+Since this chain returns to its starting point, it is called an amicable chain.
+
+Find the smallest member of the longest amicable chain with no element exceeding one million.
\ No newline at end of file
diff --git a/www/statics/euler/euler_095_explanation.md b/www/statics/euler/euler_095_explanation.md
new file mode 100644
index 0000000..feb6a76
--- /dev/null
+++ b/www/statics/euler/euler_095_explanation.md
@@ -0,0 +1,11 @@
+The trick is to use a sieve to pre-calculate all the proper-divisor-sums.
+We use a big 1000x1000 array to store all the proper-divisor-sums of all numbers from one to one million.
+Initially we set all these fields to zero, then we add `1` to all multiples of `1`, the `2` to all multiples to `2` etc, etc.
+At the end we have a nice map of all the interesting numbers. (Fun fact: we have also calculated the primes, every number for which the sum is `1` is prime).
+
+Then we use a second 1000x1000 array to remember the values we have already checked.
+The rest is simply iterating through all the numbers, trying to build a chain for each one and remembering the length of the longest chain together with its smallest member.
+While doing this we track the visited values in our cache array to prevent checking the same chain multiple times.
+
+This code is not the fastest in befunge, but I honestly can't see a way to gain big performance (the same code in C# runs in 107ms).
+Most of the time is spend with building the map of the amicable values, but all approaches with calculating them on-demand where way worse than this algorithm.
\ No newline at end of file
diff --git a/www/statics/euler/euler_096.php b/www/statics/euler/euler_096.php
new file mode 100644
index 0000000..1a06b10
--- /dev/null
+++ b/www/statics/euler/euler_096.php
@@ -0,0 +1,19 @@
+ 96,
+ 'title' => 'Su Doku',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_096_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_096_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_096_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=096',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-096.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 583893708,
+ 'time' => 90918,
+ 'width' => 218,
+ 'height' => 50,
+ 'value' => 24702,
+];
diff --git a/www/statics/euler/euler_096_code.txt b/www/statics/euler/euler_096_code.txt
new file mode 100644
index 0000000..936da1c
--- /dev/null
+++ b/www/statics/euler/euler_096_code.txt
@@ -0,0 +1,50 @@
+v XX X ########### ########### ############################# ############################# 003 ... 007
+ C C # 3 17# # # # # # # 900 ... 000
+ PPPPP # 15 9 8# # # # # # # 001 ... 500
+ XXX # 6 # # # # # # # . . . .
+ LLLLLL #1 7 # # # # # # # . . .
+ PMMMM # 9 2 # # # # ########## # # # . . . .
+ MM MMM # 5 4# # # # ################## # # # 002 ... 000
+0XXX XX # 2 # # # # ################## # # #
+7 #5 6 34 # # # # ####################### # # #
+7 #34 2 # # # # ####################### # # ####### #
+* ########### ###########v<# #################### # # ############ #
+> #v # 492*+11p9:*:9*61p>1-v## ################ # # ################# #
+ >9+\9/1+p:0\:9%11g+\9/1+p:| # ############ # # ################# #
+ ^%9:\+*86%+88 g+1/9\+9%9::$#:< # ############ # # ######## ######## #
+v1/*93\+*75%*93:\0:-1+p:0\:39*%89*+\39*/#| 1#:+# p# < # #################### # # ################# #
+v p030$<>p152p::9%v # ####################### # # ############### #
+>9:*>1-:9/32p:9%22p212^vg+1/9\+9< # ####################### # # ############ #
+v10 $< > v>68*-:42pv # ####################### # # ####### #
+4 ^_^#: # 1-:9%24p:9/3v^_ v # ########## # # #
+>30g9:*-!#^_9:*^ > #4 v# ########## # # #
+ v0p450_v#!-*86 g+g431+g429p<$ ## # # #v <
+ > > :#^_$14g#v_015p v # # # # v _$:1+|
+^ p410< ## # # #1>+\g13g9 %9+13g9/1+p:^ v<
+p6 v:p45+1g44 < > ^# # # #-^+**882* 9/5g06%9g31+*9< $
+4>4p9 >1-:44p57*24g3*44g3%+v # # # # >:60p99*>1-::13p9/60g5%^ .
+1 #>|:_v#g++/3g44*3g431+ < ############################# ############################# ^ < \++-*86<@
+0 $ >64g1+64p ^|^ #># #<:77*-!#^_\91g68*-55+*55v
+ ^ < $# #< >025p035p045p9:*:*55p9:*>1-: 9%16p:9/26p916gvv+-*86g1+<
+ >64g:!#v_1-#^_14g1+14pv#> >42g68*+22g9+3 v ^ < v _v#!g54 $_^#!:<_v#<-*86g+g621+<>55+*56+1g^
+ v $$32p54g42p20g5v- >1-:13p"X"57*22g3*13g3%++132g3*13g3v >p11g2 5 g+v! ! >1+:66p57*16g3*66g1-3%v
+ >>01-::17p27p37p9:*v_$ 9v 21 vg++/3g31*3g231++%3g31*3g22*98p++/< vp210p+g 5 31<5>pv < _v#g++/3-1g66*3g621++<
+ v94p76/9:p75%9:-1<^:<<: p v _52g89*22g3*13g3%v >25g22p3 5 gv 56 : - >56g1+56p4 v
+ >2*+57g+167g+g20g- |p: > ^:|:p++/3g31*3g231++< ^ p24g54p 2 3< g4 >9^|+!`g51g66!!g6< p
+ v*86g+g761+g759<7* >$9>1-:23p"X"57*23g3*42g1-3%++132g3*42g1-3v 5^g66 <> ^5
+ >-17p57g27 p67g3^* # vg++/3-1g24*3g231++%3-1g24*3g32*98p++/< >6g`!+#^_16g25p26g35p46g45p56g5^
+ v*98p76/*93:p75%*93:-1< _$ v>^v _52g89*23g3*42g1-3%v v ># ^#<
+ >57g+167g+g20g-! #v_:^< 2 >:|:p++/3-1g24*3g231++<
+ v75*750p+g761+g75*980< :: 0v19$<>p"X"57*22g3*42g1-3%+ + 133g3*42g1-3/++v
+ >167g3/+g 68*-!| g>-:33^vg++/3-1g24*3g331++% 3 -1g24*3g22*98p <
+ ^+/3g759g+167g+p^>7g3/+p30g1-30p^ - |:< p++/3-1g24*3g331++<
+ vp51g71p+g731+g72+*2940p02 < >$9>1-::3%23p3/33p"X"57 * 22g3/3*23g+3*42g1-3%++132g3/3*33g+3*42gv
+ ^ ># # ^ v># #<^ vg++/3-1g24*3+g33* 3 /3g231++%3-1g24*3+g32*3/3g22*98p++/3-1 <
+^ $_^#!:g21$< v :_52g89*22g3/3*23g+ 3 *42g1-3%v
+ ^># ## #< ^
\ No newline at end of file
diff --git a/www/statics/euler/euler_096_description.md b/www/statics/euler/euler_096_description.md
new file mode 100644
index 0000000..44da39a
--- /dev/null
+++ b/www/statics/euler/euler_096_description.md
@@ -0,0 +1,50 @@
+Su Doku (Japanese meaning number place) is the name given to a popular puzzle concept.
+Its origin is unclear, but credit must be attributed to Leonhard Euler
+who invented a similar, and much more difficult, puzzle idea called Latin Squares.
+The objective of Su Doku puzzles, however, is to replace the blanks (or zeros)
+in a 9 by 9 grid in such that each row, column, and 3 by 3 box contains
+each of the digits 1 to 9.
+Below is an example of a typical starting puzzle grid and its solution grid.
+
+~~~~~~~~~~~~~~~~~~~~~
+0 0 3 0 2 0 6 0 0
+9 0 0 3 0 5 0 0 1
+0 0 1 8 0 6 4 0 0
+
+0 0 8 1 0 2 9 0 0
+7 0 0 0 0 0 0 0 8
+0 0 6 7 0 8 2 0 0
+
+0 0 2 6 0 9 5 0 0
+8 0 0 2 0 3 0 0 9
+0 0 5 0 1 0 3 0 0
+~~~~~~~~~~~~~~~~~~~~~
+
+~~~~~~~~~~~~~~~~~~~~~
+4 8 3 9 2 1 6 5 7
+9 6 7 3 4 5 8 2 1
+2 5 1 8 7 6 4 9 3
+
+5 4 8 1 3 2 9 7 6
+7 2 9 5 6 4 1 3 8
+1 3 6 7 9 8 2 4 5
+
+3 7 2 6 8 9 5 1 4
+8 1 4 2 5 3 7 6 9
+6 9 5 4 1 7 3 8 2
+~~~~~~~~~~~~~~~~~~~~~
+
+A well constructed Su Doku puzzle has a unique solution and can be solved by logic,
+although it may be necessary to employ "guess and test" methods in order to eliminate
+options (there is much contested opinion over this).
+The complexity of the search determines the difficulty of the puzzle;
+the example above is considered easy because it can be solved by straight forward
+direct deduction.
+
+The 6K text file, [sudoku.txt](https://projecteuler.net/project/resources/p096_sudoku.txt) (right click and 'Save Link/Target As...'),
+contains fifty different Su Doku puzzles ranging in difficulty,
+but all with unique solutions (the first puzzle in the file is the example above).
+
+By solving all fifty puzzles find the sum of the 3-digit numbers found in the top
+left corner of each solution grid; for example, 483 is the 3-digit number found in the
+top left corner of the solution grid above.
\ No newline at end of file
diff --git a/www/statics/euler/euler_096_explanation.md b/www/statics/euler/euler_096_explanation.md
new file mode 100644
index 0000000..31671e9
--- /dev/null
+++ b/www/statics/euler/euler_096_explanation.md
@@ -0,0 +1,11 @@
+This problem boils down to implementing a sudoku solver.
+So thats what I did (initially as a stand-alone project).
+And then I wrote a program around that inputs the 5 puzzles
+into the solver and calculates the result.
+
+This means in this post I'm trying to describe how to build a sudoku solver in befunge.
+
+Because all the logic is practically a stand-alone sudoku solver, I simply wrote one. You can read about the development and a few of my design decisions in [this blogpost here](https://www.mikescher.com/blog/9/A_complete_sudoku_solver_in_Befunge93).
+The rest was looping 50 times through the solver code and adding the results together.
+
+Really all the interesting stuff is written in the blogpost about the sudoku solver, go read it!
\ No newline at end of file
diff --git a/www/statics/euler/euler_097.php b/www/statics/euler/euler_097.php
new file mode 100644
index 0000000..69d0425
--- /dev/null
+++ b/www/statics/euler/euler_097.php
@@ -0,0 +1,19 @@
+ 97,
+ 'title' => 'Large non-Mersenne prime',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_097_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_097_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_097_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=097',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-097.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 164439636,
+ 'time' => 21091,
+ 'width' => 13,
+ 'height' => 5,
+ 'value' => 8739992577,
+];
diff --git a/www/statics/euler/euler_097_code.txt b/www/statics/euler/euler_097_code.txt
new file mode 100644
index 0000000..449780a
--- /dev/null
+++ b/www/statics/euler/euler_097_code.txt
@@ -0,0 +1,5 @@
+"z~k"+*7+98v@
+v +***"Gqz"<.
+>1- \2*"(2"v%
+|: \%*:** :<*
+>$1+"(2":**:^
\ No newline at end of file
diff --git a/www/statics/euler/euler_097_description.md b/www/statics/euler/euler_097_description.md
new file mode 100644
index 0000000..a877fda
--- /dev/null
+++ b/www/statics/euler/euler_097_description.md
@@ -0,0 +1,8 @@
+The first known prime found to exceed one million digits was discovered in 1999,
+and is a Mersenne prime of the form `2^6972593?1`;
+it contains exactly 2,098,960 digits.
+Subsequently other Mersenne primes, of the form `2^p?1`, have been found which contain more digits.
+
+However, in 2004 there was found a massive non-Mersenne prime which contains 2,357,207 digits: `28433*2^7830457+1`.
+
+Find the last ten digits of this prime number.
\ No newline at end of file
diff --git a/www/statics/euler/euler_097_explanation.md b/www/statics/euler/euler_097_explanation.md
new file mode 100644
index 0000000..60db0b4
--- /dev/null
+++ b/www/statics/euler/euler_097_explanation.md
@@ -0,0 +1,16 @@
+Well this was a really easy one.
+We simply multiply the number `28433` 7830457-times with two.
+After each multiplication we modulo the result with 2^10 to prevent an overflow and in the end we add one.
+This is really simple (the program operates completely on the stack) and works perfectly as long as our interpreter uses at least 64bit numbers.
+(But this is a condition for a lot of programs I have written here)
+
+But just for fun I have written an alternative version that uses only 32bit numbers.
+You can find it on github under `Euler_Problem-097 (32bit).b93`, or here:
+
+~~~~~~~~~~~~
+"}}2( "****04003pp201p102p>04g01g2*`#v_v
+Xv2*2g10**!%3*g20-2g10!-1%3*g102`2g10< 0
+X>-*03g+03p01g2*3%2-!01g2+# 02g*3%v 3
+Xv*2g10+*2g20g10p30+g30*+* g1022*!< @.g<
+C>02g3*+01p02p ^
+~~~~~~~~~~~~
\ No newline at end of file
diff --git a/www/statics/euler/euler_098.php b/www/statics/euler/euler_098.php
new file mode 100644
index 0000000..08f2f53
--- /dev/null
+++ b/www/statics/euler/euler_098.php
@@ -0,0 +1,19 @@
+ 98,
+ 'title' => 'Anagramic squares',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_098_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_098_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_098_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=098',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-098.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 145592567,
+ 'time' => 22714,
+ 'width' => 258,
+ 'height' => 199,
+ 'value' => 18769,
+];
diff --git a/www/statics/euler/euler_098_code.txt b/www/statics/euler/euler_098_code.txt
new file mode 100644
index 0000000..156e755
--- /dev/null
+++ b/www/statics/euler/euler_098_code.txt
@@ -0,0 +1,54 @@
+vXXX # #################################################################################################### # A
+ XXX # #################################################################################################### # ACCESS
+ XX # #################################################################################################### # ACROSS
+ XX # #################################################################################################### # ADDITIONAL
+ XXX # #################################################################################################### # ADVISE
+ X # #################################################################################################### # AGAINST
+ # #################################################################################################### # AIM
+ # #################################################################################################### # ALRIGHT
+ # #################################################################################################### # ANALYSIS
+ $ # #################################################################################################### # ANYBODY
+ #################################################################################################### # APPEARANCE
+ #################################################################################################### # ARGUE
+ #################################################################################################### # ART
+ #################################################################################################### # ASSET
+ #################################################################################################### # ATTEMPT
+0 #################################################################################################### # AVAILABLE
+1 #################################################################################################### # BACKGROUND
+9 #################################################################################################### # BASIC
+p v \< v !:\< # BED
+>0>:: 0\ :9%82**"r"+\9/ 10p>:1+\10gg:84*-#^_$$ 0\:!vv-1\5< v*\<+ # BELONG
+ v <>: >| >\:|$ # BIG
+ | -*"&/" :+1 p /"d"\+9%"d": \$_"A"-0\: ^$>| >^ # BLOODY
+ $ >:#<^>1\^ v \+1\< # BOTH
+ >011p>11g1+21p >11g:"d"%9+\"d"/g 21g:"d"%9+\"d"/g - #v_ 11g:9%82**"r"+\9/10p0\>:1+\10gg84*-#^_v # BRIDGE
+>"&/"*-| |!`*"&/"p12:+1g12 < < >\*v >55+\1-v >\*v >55+\1-v $ # BURN
+^ p11:+1p/"d"\+9%"d":\"#":g11< |:\< |:< < |:\< |:< < # CAMPAIGN
+ 9 v p02:p010-1 \ -1$< ^$< ^ \0 \ $< ^$< ^ \0-1p13::< ...
+ g vp01g03_v#-g01:_v#- < ...
+ . >:30p:20 g\/+2/: 30g^ vp01g03_v#-g01:_v#- < ...
+ @ > >$30g1+12p 010p:20p>:30p:20 g\/+2/: 30g^
+ ^ < > >$30gv
+ vp\"n"\"|":<+*297:1-\ | >:1-\ | > 13g1+:13p ^
+ v-"A"g/9\+g41+"r"**28%9:g11 : >| >\:| >v >v
+ >24p 31g1-14g- 0\: ^>$:| > $23g\/55+%34p "n"24gg:"|"-|>34g-|> 534gg:"|"-|>24g-|
+ >1\^ >$ v >$ v
+ v p410p510< vpg42"n"g43< vpg435+"A"g42<
+ >v > ^ > ^
+ >21g:9%82**"r"+14g+\9/g"A"-24p"n"24gg"|"-!|> >> ^
+ >"n"24gg14g+!|
+ |-g13p41:+1g41 p51+gg42"n"*+55g51<
+ > ^
+ >15g23g` 15g19g` * !| > 15g19p v
+ 1 > >$30gv> | > ^
+ 5 vp01g03_^#-g01:_^#- <: > ^
+ g >:30p:20 g\/+2/: 30g^*
+ > >#^ #p #0 2 #<$ v
+ > :88*%"9"`#^_:88+%:9`#v_:2-#v_v 2
+ > > > > # >$>$0^
+ |!-8_^#-7:_^#-6:_^#-5:_^# -3:< g
+ > ^< 0 <^:p010 <^<-!
+ >:55+%:7-!#^_:3-!#^_2-!#^_:3%2-#^_^>^
\ No newline at end of file
diff --git a/www/statics/euler/euler_098_description.md b/www/statics/euler/euler_098_description.md
new file mode 100644
index 0000000..cf1aa73
--- /dev/null
+++ b/www/statics/euler/euler_098_description.md
@@ -0,0 +1,16 @@
+By replacing each of the letters in the word CARE with 1, 2, 9, and 6 respectively,
+we form a square number: 1296 = 36^2. What is remarkable is that,
+by using the same digital substitutions, the anagram, RACE,
+also forms a square number: 9216 = 96^2.
+We shall call CARE (and RACE) a square anagram word pair and specify further
+that leading zeroes are not permitted,
+neither may a different letter have the same digital value as another letter.
+
+Using [words.txt](https://projecteuler.net/project/resources/p098_words.txt),
+a 16K text file containing nearly two-thousand common English words,
+find all the square anagram word pairs
+(a palindromic word is NOT considered to be an anagram of itself).
+
+What is the largest square number formed by any member of such a pair?
+
+NOTE: All anagrams formed must be contained in the given text file.
\ No newline at end of file
diff --git a/www/statics/euler/euler_098_explanation.md b/www/statics/euler/euler_098_explanation.md
new file mode 100644
index 0000000..8c83d6a
--- /dev/null
+++ b/www/statics/euler/euler_098_explanation.md
@@ -0,0 +1,51 @@
+With this problem I tried a little bit differen methology with designing the problem.
+Programs with massive (16k) input are always kind of ugly in befunge because
+all of the data must be in the program code, so I thought I can at least try a little bit around.
+
+In this program I seperated the code, as much as I could, into independent subprograms.
+All subprograms can use the [1,0]-[9,0] fields as temporary values, get their input
+from the stack and write their output also to the stack.
+Then I combined them together to build the whole program.
+
+All the subprograms are in my [BefungePrograms git repo](https://gogs.mikescher.com/gitmirror/BefungePrograms)
+
+This resulted in more readable code and (hopefully) snippets that I can reuse in other programs.
+But the code doesn't compress as good (which nobody cares about in this problem, cause of the giant input size)
+and I'm sure I could optimize it a lot by using more global state and shared variables etc.
+
+I think for my next programs I will continue as I did before and sometimes use independent code snippets
+(for example for the integer-squareroot function) but for the big main program I will write it all together.
+
+The program works like so:
+
+1. First we calculate a "palindromic hash value" for each input word, this is a hash algorithm that
+ has no collisions as long as there are max five repeated letters in a word and has the same value for
+ palindroms.
+ Practically it is a 26-digit number in base-5 where each digit denotes the amount a specific letter occurs in our word.
+ We can not use a larger number than 5 for our base because then we would overflow our 64bit numbers.
+
+2. Next we go through our palindromic list and search for palindroms (words with the same hash)
+ With some clever sorting tricks we could do this in `log2(n)`, but I will leave this as an
+ exercise for ther reader and and implement in naively in `n^2`
+
+3. For each word we iterate through all the squares with the correct digit count.
+ This means we start with `j`, where `j = 10^(len - 1)` and wnd with `k`, where `k = (10^len) - 1`
+
+4. Now (for each square) we can generate the numeric value for word B with word A + square as our map.
+ When we generate our char->digit map (as an 26 element array) we also generate a digit->char map
+ to test if any digit is mapped to multiple different characters (a failure criteria)
+
+5. Now we have square A and (possible) square B, with our optimized is-integer-squareroot function from problem 086
+ we test if B is a square number. And if this is the case (and B is bigger than our current candidate) we set B
+ as our current result candidate
+
+6. After we have done this for all pairs we can return (= print out) our current best candidate.
+
+
+Used sub programs:
+ - fixed_base_pow.b93
+ - read_single_word.b93
+ - get_palindromic_hash.b93
+ - integer-squareroot-2.b93
+ - is-squarenumber.b93
+ - length_single_word.b93
\ No newline at end of file
diff --git a/www/statics/euler/euler_099.php b/www/statics/euler/euler_099.php
new file mode 100644
index 0000000..73ff0e9
--- /dev/null
+++ b/www/statics/euler/euler_099.php
@@ -0,0 +1,19 @@
+ 99,
+ 'title' => 'Largest exponential',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_099_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_099_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_099_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=099',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-099.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => true,
+ 'steps' => 5072021,
+ 'time' => 1107,
+ 'width' => 63,
+ 'height' => 1000,
+ 'value' => 709,
+];
diff --git a/www/statics/euler/euler_099_code.txt b/www/statics/euler/euler_099_code.txt
new file mode 100644
index 0000000..d7412dd
--- /dev/null
+++ b/www/statics/euler/euler_099_code.txt
@@ -0,0 +1,23 @@
+v$$$$$$ 519432,525806
+ XX 00v $< 632382,518061
+ v 0:5 1p vv <1 466580,530130
+ v $ $ ## > 0"2">:11gg:48*-0`!#^_:","- | 525895,525320
+^p110p16< ^ # +1\0$< 15991,714883
+ vp04+g04 < vp06< + 960290,502358
+ : #>1-#v\#/ #2<^ <: 1 760018,511029
+ !v<| :\<***"@}}"g01<>$ ^ g 166800,575487
+v_ 20p10p01>:2*10g`| |>1^ 210884,564478
+$ >$30p0:4v^\+1\*2 v p05p0< >>$40#+v 681146,515199
+1 0#>030g"}}@"**`!|^ $< *g 563395,522587
+g g|!`g03***"@}}"21+30g:*"}}@"**/30^ $00 923525,503780
+@ >50p30g2/30p20g50g>:!|6g 595148,520429
+ > #2/#\\#-^#1<^< 177108,572629
+ 750923,511482
+ 440902,532446
+ 881418,505504
+ ...
+ ...
\ No newline at end of file
diff --git a/www/statics/euler/euler_099_description.md b/www/statics/euler/euler_099_description.md
new file mode 100644
index 0000000..f759584
--- /dev/null
+++ b/www/statics/euler/euler_099_description.md
@@ -0,0 +1,11 @@
+Comparing two numbers written in index form like 2^11 and 3^7 is not difficult,
+as any calculator would confirm that 2^11 = 2048 < 3^7 = 2187.
+
+However, confirming that 632382^518061 > 519432^525806 would be much more difficult,
+as both numbers contain over three million digits.
+
+Using [base_exp.txt](https://projecteuler.net/project/resources/p099_base_exp.txt),
+a 22K text file containing one thousand lines with a base/exponent pair on each line,
+determine which line number has the greatest numerical value.
+
+NOTE: The first two lines in the file represent the numbers in the example given above.
\ No newline at end of file
diff --git a/www/statics/euler/euler_099_explanation.md b/www/statics/euler/euler_099_explanation.md
new file mode 100644
index 0000000..82f9441
--- /dev/null
+++ b/www/statics/euler/euler_099_explanation.md
@@ -0,0 +1,38 @@
+For every number we normalize the Exponentiation to base 2.
+(We search the equivalent Power `2^x`).
+And then we only compare the exponents with each other, practically this
+means we compare the length of the number in binary representation.
+
+We chose 2 as our base because this way we don't have to worry too much about
+the precision of our calculations (befunge has no native floating point values).
+If we would have found two entries with the same (overall highest) exponent, we would
+have to calculate the exponent to a higher precision, but fortunately this did not happen.
+
+From `b^e` we can get the normalized fraction `2^(e * log2(b))`.
+But because befunge has no log2 operator we have to go through the dirty work of manually approximating log2.
+
+We use [this][1] algorithm to calculate log2.
+
+First we calculate the integer part by simple searching the biggest number `2^n` where `2^n < b`
+
+Then the real part equals `log2(2^(-n) * b)`, because we don't want to caclulate with real numbers we
+insert a Precision factor `F` (in this program we used a value of 1 million).
+
+Now `y = 2^-n * b` and `rp = log2(y)`. We calculate y by dividing b n-times with two.
+
+Our final result will be `r = n * e + rp * e`. We can already calculate `n*e`, the only missing part is `rp*e`,
+which we will call `exporp`.
+
+Then we repeat the following steps until the value of exporp is no longer changing:
+
+ - count the number of times `m` we have to square `y` until `y >= 2`
+ - `y = y^(2^m) / 2`
+ - add `m` to `msum`, the collective sum of all calculated `m` values until now
+ - divide `e` `msum`-times by two and add the result to `exporp`
+
+Now we have calculated `exporp`, our result is `r = n * e + exporp`.
+
+With this method we can calculate the exponent of our normalized exponentiation.
+Next we simply iterate through the whole inpt and search the line number with the greatest base2-exponent.
+
+[1]: https://en.wikipedia.org/wiki/Binary_logarithm#Iterative_approximation
\ No newline at end of file
diff --git a/www/statics/euler/euler_100.php b/www/statics/euler/euler_100.php
new file mode 100644
index 0000000..007a1d3
--- /dev/null
+++ b/www/statics/euler/euler_100.php
@@ -0,0 +1,19 @@
+ 100,
+ 'title' => 'Arranged probability',
+ 'description' => function(){ return file_get_contents(__DIR__ . '/euler_100_description.md'); },
+ 'code' => function(){ return file_get_contents(__DIR__ . '/euler_100_code.txt'); },
+ 'explanation' => function(){ return file_get_contents(__DIR__ . '/euler_100_explanation.md'); },
+ 'url_euler' => 'http://projecteuler.net/problem=100',
+ 'url_raw' => 'https://raw.githubusercontent.com/Mikescher/Project-Euler_Befunge/master/processed/Euler_Problem-100.b93',
+ 'url_github' => 'https://github.com/Mikescher/Project-Euler_Befunge',
+ 'abbreviated' => false,
+ 'steps' => 1649,
+ 'time' => 0,
+ 'width' => 56,
+ 'height' => 3,
+ 'value' => 756872327473,
+];
diff --git a/www/statics/euler/euler_100_code.txt b/www/statics/euler/euler_100_code.txt
new file mode 100644
index 0000000..34602aa
--- /dev/null
+++ b/www/statics/euler/euler_100_code.txt
@@ -0,0 +1,3 @@
+10v>012p >01g11g:01g3*\4*+01p3*\2*+11p02g12g:02g3*\4*-0v
+##1^p110<|!`*:**"@}}"/4-g20-*g212-g10+*2g112p21-*2\*3p2<
+##>p102p^>402g2*+12g2*+01g2*+11g2*-8/.@
\ No newline at end of file
diff --git a/www/statics/euler/euler_100_description.md b/www/statics/euler/euler_100_description.md
new file mode 100644
index 0000000..68c84b1
--- /dev/null
+++ b/www/statics/euler/euler_100_description.md
@@ -0,0 +1,9 @@
+If a box contains twenty-one coloured discs, composed of fifteen blue discs and six red discs,
+and two discs were taken at random, it can be seen that the probability of taking two blue discs,
+`P(BB) = (15/21)x(14/20) = 1/2`.
+
+The next such arrangement, for which there is exactly 50% chance of taking two blue discs at random,
+is a box containing eighty-five blue discs and thirty-five red discs.
+
+By finding the first arrangement to contain over `10^12 = 1,000,000,000,000` discs in total,
+determine the number of blue discs that the box would contain.
\ No newline at end of file
diff --git a/www/statics/euler/euler_100_explanation.md b/www/statics/euler/euler_100_explanation.md
new file mode 100644
index 0000000..c0b9a1a
--- /dev/null
+++ b/www/statics/euler/euler_100_explanation.md
@@ -0,0 +1,57 @@
+Let's say `b` is the number of blue disks, `r` the number of red disks
+and `n` is the total number.
+From the problem description we can infer this:
+~~~
+b+r = n (1)
+0 < b < n (2)
+0 < r < n (3)
+n > 10^12 (4)
+(b/n)*((b-1)/(n-1)) = 1/2 (5)
+~~~
+
+Now we can user (1) and (2) to get a formula for `b` and `n`:
+
+~~~
+(b/n)*((b-1)/(n-1)) = 1/2
+2*b*(b-1) = n * (n-1)
+2*b^2 - 2*b = n^2 - n
+2 * (b^2 - b) = n^2-n
+0.5 * (2b)^2 - (2b) = (n)^2 - (n)
+2*(b^2) - 2b = (n)^2 - (n)
+
+b = 1/2 ( sqrt(2n^2 - 2n + 1) + 1 )
+~~~
+
+For the last formula we search for integer solutions.
+We can now either solve this manually with diophantine equations,
+or we ask [Wolfram|Alpha](www.wolframalpha.com/input/?i=2*b*b-2b+%3D+n*n-n).
+Which gives us the following two formulas:
+
+~~~
+s = sqrt(2)
+
+b = (1/8) * ( 2*(3-2*s)^m + s*(3-2*s)^m + 2*(3+2*s)^m - s*(3+2*s)^m + 4)
+n = (1/4) * ( -(3-2*s)^m - s*(3-2*s)^m - (3+2*s)^m + s*(3+2*s)^m + 2)
+
+m element Z, m >= 0
+~~~
+
+We can see both formulas contain the expression sqrt(2), which is not
+only fractional but also irrational. Which is a problem with the strict integer
+operations in befunge.
+
+But we can sidestep this by using a special number notation `r * 1 + s * sqrt(2)`.
+In every step we calculate the "real" part of the number plus a multiple of `sqrt(2)`.
+This is kinda like the common notation of [imaginary numbers](https://en.wikipedia.org/wiki/Imaginary_number).
+
+Now all we have to do is create algorithms for addition and multiplication in our new number format.
+
+~~~
+(r1 + s1 * sqrt(2)) + (r2 + s2 * sqrt(2)) = (r1+r2) + (s1+s2) * sqrt(2)
+(r1 + s1 * sqrt(2)) * (r2 + s2 * sqrt(2)) = (r1*r2+2*s1*s2) + (s1*r2+r1*s2) * sqrt(2)
+~~~
+
+Now we can use the formulas from Wolfram|Alpha until we find a value for `n > 10^12`.
+
+In the end this problem wasn't that hard to code when all the preparations were done.
+Also it's pretty fast.
\ No newline at end of file
diff --git a/www/statics/programs/All in One.php b/www/statics/programs/All in One.php
new file mode 100644
index 0000000..9cc7449
--- /dev/null
+++ b/www/statics/programs/All in One.php
@@ -0,0 +1,18 @@
+ 'All in One',
+ 'category' => 'Tool',
+ 'stars' => 1,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'A little \"swiss army knife\" programm with over 100 different functionalities',
+ 'add_date' => '2008-11-26',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/All in One_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/All in One.png',
+];
diff --git a/www/statics/programs/All in One_description.md b/www/statics/programs/All in One_description.md
new file mode 100644
index 0000000..be3b872
--- /dev/null
+++ b/www/statics/programs/All in One_description.md
@@ -0,0 +1,25 @@
+All in One is a multifunctional tool with many, many features.
+In fact it's a Compendium of everything we found useful and easy to implement (or easy to copy the code from somewhere ...).
+
+It's developed by Benjamin Rottler and myself in the glorious language `Delphi`.
+
+## Highlights
+
+- Show registered file extensions
+- Shutdown PC, Restart PC
+- Change the size and text of the start-button
+- Change the system time
+- Disable the screensaver
+- Read your system rights
+- Show runnign processes
+- Hide multiple system elements (taskbar, clock, TNA, startbutton ...)
+- List installed software
+- Show Mac address, ip address, ie version, win version
+- Get Special windows paths
+- Set any window to fullscreen
+- Maximize, minimize, hide, kill, highlight any window
+- Convert Roman numbers and arabic numbers into each other
+- Execute cmd-commands
+- List all window captions
+- Delete itself (without a trace)
+- Make a screenshot
\ No newline at end of file
diff --git a/www/statics/programs/Beepster.php b/www/statics/programs/Beepster.php
new file mode 100644
index 0000000..b332800
--- /dev/null
+++ b/www/statics/programs/Beepster.php
@@ -0,0 +1,19 @@
+ 'Beepster',
+ 'category' => 'Hoax',
+ 'stars' => 0,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Annoy your teachers/freinds with a very high pitched sound, even without external" +
+ " speakers.',
+ 'add_date' => '2008-06-04',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Beepster_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Beepster.png',
+];
diff --git a/www/statics/programs/Beepster_description.md b/www/statics/programs/Beepster_description.md
new file mode 100644
index 0000000..b6a4fb7
--- /dev/null
+++ b/www/statics/programs/Beepster_description.md
@@ -0,0 +1,4 @@
+Beepster is a - relatively stupid - little tool to create a really high pitched sound with your computer.
+
+The special trick is that the beep is not created by you normal speakers, but by your internal ones.
+So the only requirement is that you computer has an internal speaker (its the one that creates the error beeps, for example when booting up fails)
\ No newline at end of file
diff --git a/www/statics/programs/BefunUtils.php b/www/statics/programs/BefunUtils.php
new file mode 100644
index 0000000..cdcbd5a
--- /dev/null
+++ b/www/statics/programs/BefunUtils.php
@@ -0,0 +1,19 @@
+ 'BefunUtils',
+ 'category' => 'Compiler',
+ 'stars' => 4,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C#',
+ 'short_description' => 'My selfmade Code-to-Befunge93 compiler, with a few little extras.',
+ 'add_date' => '2014-08-04',
+ 'urls' =>
+ [
+ 'github' => 'https://github.com/Mikescher/BefunUtils',
+ 'wiki' => 'https://github.com/Mikescher/BefunUtils/wiki',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/BefunUtils_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/BefunUtils.png',
+];
diff --git a/www/statics/programs/BefunUtils_description.md b/www/statics/programs/BefunUtils_description.md
new file mode 100644
index 0000000..a567031
--- /dev/null
+++ b/www/statics/programs/BefunUtils_description.md
@@ -0,0 +1,73 @@
+BefunUtils
+========
+
+This is my collection of tools, libraries and transcompilers for the esoteric programming language [Befunge](http://esolangs.org/wiki/Befunge).
+
+It consists of the following core components:
+
+### [BefunGen](https://github.com/Mikescher/BefunGen):
+> A Befunge-93 to multiple procedural languages (c, java, csharp, python) transcompiler
+
+### [BefunWrite](https://github.com/Mikescher/BefunWrite):
+> A small editor for Textfunge, the language used by BefunGen - use this if you want to try BefunGen for yourself
+
+### [BefunHighlight](https://github.com/Mikescher/BefunHighlight):
+> A dynamic Befunge-93 syntax highlighting library. Highlights your sourcecode intelligent and context-sensitive
+
+### [BefunExec](https://github.com/Mikescher/BefunExec):
+> A (fast) Befunge-93 interpreter and debugger
+
+### [BefunRep](https://github.com/Mikescher/BefunRep):
+> A tool to calculate (the best) number-representation in Befunge-93 space
+
+### [BefunCompile](https://github.com/Mikescher/BefunCompile):
+> An *(non-general)* Befunge-93 compiler. Compile your Befunge-93 code to C, C# or Python
+
+### [BefunRun](https://github.com/Mikescher/BefunRun):
+> A simple terminal tool to run a befunge93 program (with extended grid size) and output its output.
+
+### [BefunDebug](https://github.com/Mikescher/BefunDebug):
+> A debug and test tool for BefunGen, BefunCompile, BefunHighlight, etc
+
+
+Set up
+==========
+
+You can either download the binaries from [www.mikescher.com](http://www.mikescher.com/programs/view/BefunUtils).
+
+Or you can setup the Solution by yourself:
+
+- Clone the **BefunUtils** repository
+- Clone all the subproject repositories into subfolder *(or simply execute CLONE_ALL.bat)*
+- *(eg clone BefunExec into the folder /BefunExec)*
+- Open the solution file in Visual Studio *(or build all projects with the BUILD_ALL.bat script)*
+
+Screenshots
+==========
+
+BefunExec:
+
+
+BefunWrite:
+
+
+BefunRep:
+
+
+BefunHighlight:
+
+
+BefunCompile:
+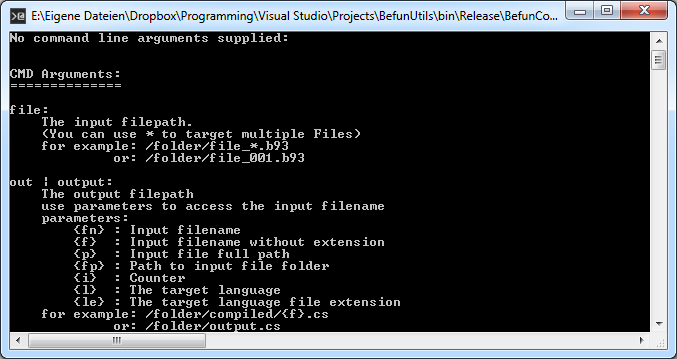
+
+BefunCompile (Graph display of [Euler_Problem-002](https://github.com/Mikescher/Project-Euler_Befunge/blob/master/Euler_Problem-002.b93) Level **0**) *(via [BefunDebug](https://github.com/Mikescher/BefunDebug))*:
+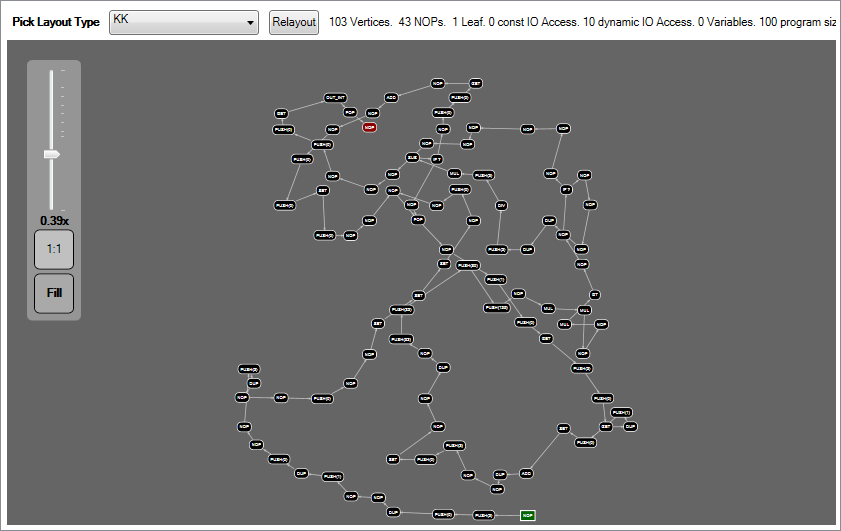
+
+BefunCompile (Graph display of [Euler_Problem-002](https://github.com/Mikescher/Project-Euler_Befunge/blob/master/Euler_Problem-002.b93) Level **2**) *(via [BefunDebug](https://github.com/Mikescher/BefunDebug))*:
+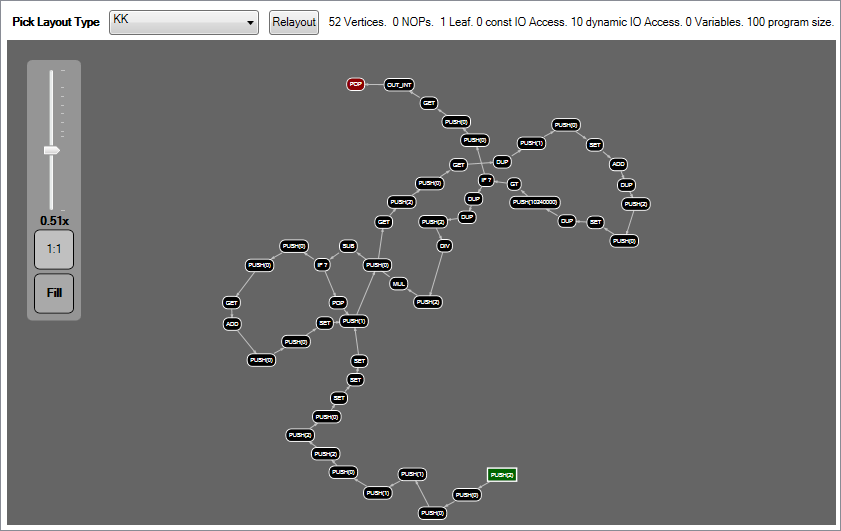
+
+BefunCompile (Graph display of [Euler_Problem-002](https://github.com/Mikescher/Project-Euler_Befunge/blob/master/Euler_Problem-002.b93) Level **3**) *(via [BefunDebug](https://github.com/Mikescher/BefunDebug))*:
+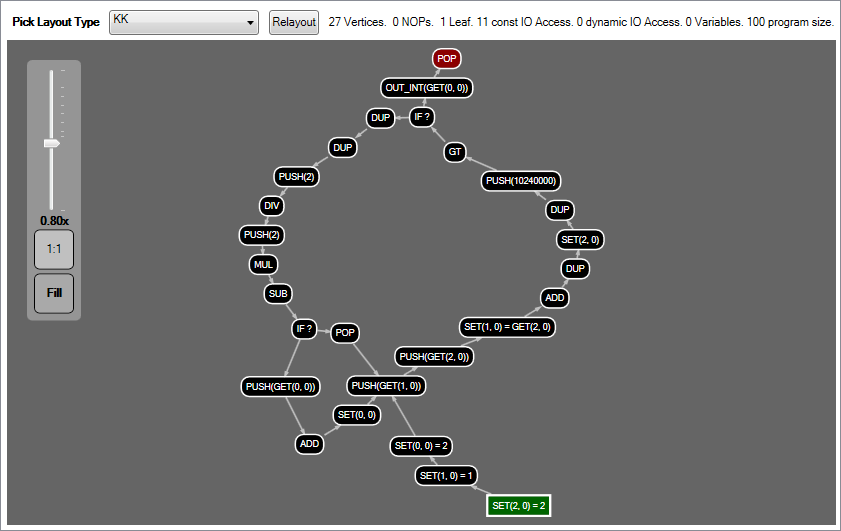
+
+BefunCompile (Graph display of [Euler_Problem-002](https://github.com/Mikescher/Project-Euler_Befunge/blob/master/Euler_Problem-002.b93) Level **5**) *(via [BefunDebug](https://github.com/Mikescher/BefunDebug))*:
+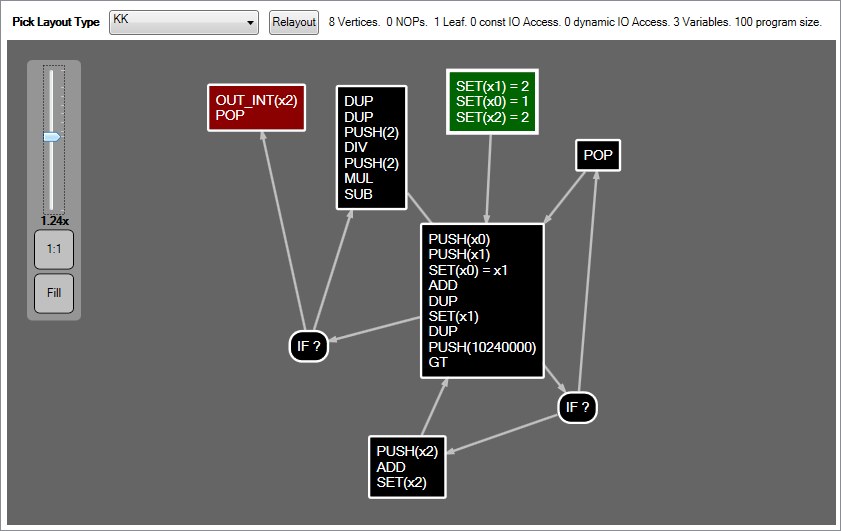
diff --git a/www/statics/programs/BefunZ.php b/www/statics/programs/BefunZ.php
new file mode 100644
index 0000000..5d459c2
--- /dev/null
+++ b/www/statics/programs/BefunZ.php
@@ -0,0 +1,18 @@
+ 'BefunZ',
+ 'category' => 'Interpreter',
+ 'stars' => 3,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C#',
+ 'short_description' => 'A Befunge-93 Interpreter compatible with Befunge-98 dimensions.',
+ 'add_date' => '2013-05-03',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/BefunZ_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/BefunZ.png',
+];
diff --git a/www/statics/programs/BefunZ_description.md b/www/statics/programs/BefunZ_description.md
new file mode 100644
index 0000000..3b9cb8f
--- /dev/null
+++ b/www/statics/programs/BefunZ_description.md
@@ -0,0 +1,4 @@
+BefunZ is a little console Befunge-93 interpreter.
+It understands all of the Befunge-93 syntax, but is not restricted to the size limitations of Befunge-93 (because they are really annoying).
+
+This is one of my first C# programs, so please be gentle and don't expect too much :)
\ No newline at end of file
diff --git a/www/statics/programs/Blitzer.php b/www/statics/programs/Blitzer.php
new file mode 100644
index 0000000..de434ea
--- /dev/null
+++ b/www/statics/programs/Blitzer.php
@@ -0,0 +1,18 @@
+ 'Blitzer',
+ 'category' => 'Hoax',
+ 'stars' => 0,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Hoax you teachers/friends with flashing lights on your monitor.',
+ 'add_date' => '2008-05-05',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Blitzer_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Blitzer.png',
+];
diff --git a/www/statics/programs/Blitzer_description.md b/www/statics/programs/Blitzer_description.md
new file mode 100644
index 0000000..4988846
--- /dev/null
+++ b/www/statics/programs/Blitzer_description.md
@@ -0,0 +1,4 @@
+Blitzer is - again - a little and probably nonsense Hoax tool.
+It makes your screen flash in black and white, so it kinda looks like something broke.
+
+Could be useful to scare people who don't know `Alt`+`F4` :D
\ No newline at end of file
diff --git a/www/statics/programs/Borderline Defense.php b/www/statics/programs/Borderline Defense.php
new file mode 100644
index 0000000..08e708d
--- /dev/null
+++ b/www/statics/programs/Borderline Defense.php
@@ -0,0 +1,19 @@
+ 'Borderline Defense',
+ 'category' => 'Game',
+ 'stars' => 4,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Java',
+ 'short_description' => 'A improved Space-Invaders clone - programmed from the Java-AG, Oken.',
+ 'add_date' => '2012-05-24',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ 'homepage' => 'http://borderlinedefense.99k.org/',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Borderline Defense_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Borderline Defense.png',
+];
diff --git a/www/statics/programs/Borderline Defense_description.md b/www/statics/programs/Borderline Defense_description.md
new file mode 100644
index 0000000..37cdf6c
--- /dev/null
+++ b/www/statics/programs/Borderline Defense_description.md
@@ -0,0 +1,12 @@
+Borderline Defense is the final project of the java AG 2012 from the OKEN Gymnasium.
+The java AG is a little student project group by [Benjamin Rottler](http://benjaminrottler.de/) and myself.
+
+Most of the code and all of the graphics were created by the students. They settled on the idea of creating a space invaders clone with a few unique features.
+Because we didn't wanted to get too much into optimizations and smaller problems we use my pre-existing game engine [absCanvas](/programs/view/absCanvas).
+
+Borderline Defense shows it strengths in:
+
+- 20 different designed levels and 10 different upgrade stages for your ship
+- An endless gameplay wich gets harder and harder with time.
+- An competitive online highscore where you can compare yourself with many others
+
diff --git a/www/statics/programs/Crystal Grid.php b/www/statics/programs/Crystal Grid.php
new file mode 100644
index 0000000..bba2bac
--- /dev/null
+++ b/www/statics/programs/Crystal Grid.php
@@ -0,0 +1,18 @@
+ 'Crystal Grid',
+ 'category' => 'Game',
+ 'stars' => 4,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Java',
+ 'short_description' => 'A challenging, tactical mini-game in blueprint-style.',
+ 'add_date' => '2013-01-03',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Crystal Grid_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Crystal Grid.png',
+];
diff --git a/www/statics/programs/Crystal Grid_description.md b/www/statics/programs/Crystal Grid_description.md
new file mode 100644
index 0000000..a0287e9
--- /dev/null
+++ b/www/statics/programs/Crystal Grid_description.md
@@ -0,0 +1,41 @@
+CrystalGrid is again an [absCanvas](/programs/view/absCanvas)-game by me.
+The game is a tactical "warfare" simulator, if you want to call it that way.
+Practically its about fastly killing the enemy cannons with your own. On the way to your target you ccan conquer neutral cannons and assimilate enemy cannons.
+
+Your enemy is a KI (even so I plan to implement a player-vs-player mode) with 4 different difficulties.
+While you are probably able to easily beat all 38 levels on `Easy` it gets harder with every difficulty.
+The final setting `Impossible` becomes a real challenge, and at the time I wrote this nobody has beaten every level in this setting. (Even so it's definitely not impossible :D )
+
+A little gimmick is the KI-vs-KI where you can watch th level played only by computer controlled players
+
+### Instructions
+
+You start with one ore more of your own cannon type.
+This cannon will immediately start shooting, you can change the direction by draggging the cannon.
+
+Your own cannon is green, neutral cannons (that don't belong to any player) are gray and enemy cannons have their respective team color (red for a single computer enemy).
+
+Every cannon has a regenerating health meter, only if a cannon has full health it will shoot. Shoot at other cannons to decrease their life if they are enemies, or increase their life if they are on your side.
+
+A zero health cannon becomes neutral once again, so you can assimilate a enemy cannon by first decreasing their *(enemy)* health to zero and then increasing *(your own)* health back to full.
+
+You can eliminate enemy bullets by shooting at them, they will destroy each other.
+
+You can "charge" your won cannons by shooting at them, their shooting speed will increase with every cannon feeding into them.
+
+You win the game when you assimilate the last active enemy cannon.
+You loose the game when you loose your last cannon.
+
+### Tips & Tricks
+
+When two equal players shoot at a neutral cannon the first hit will decide the win because the cannons auto-regeneration will help him out.
+
+Neutral cannons try (badly) to defend themselve, try to use that to your advantage.
+
+Your cannons do have a maximum shooting speed, it may be more wisely to spread your power onto multiple cannons.
+
+Be aware that your own bullets bounce from each other, fights can become really messy that way.
+
+Slow down the speed in critical moments.
+
+There are different kinds of wall, some destroy your bullets and some just reflect them, this ciuld be a strategical advantage.
\ No newline at end of file
diff --git a/www/statics/programs/Deal or no Deal.php b/www/statics/programs/Deal or no Deal.php
new file mode 100644
index 0000000..afef541
--- /dev/null
+++ b/www/statics/programs/Deal or no Deal.php
@@ -0,0 +1,18 @@
+ 'Deal or no Deal',
+ 'category' => 'Game',
+ 'stars' => 0,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'A digital version of the same-named german tv-show game.',
+ 'add_date' => '2008-10-08',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Deal or no Deal_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Deal or no Deal.png',
+];
diff --git a/www/statics/programs/Deal or no Deal_description.md b/www/statics/programs/Deal or no Deal_description.md
new file mode 100644
index 0000000..c95d2c4
--- /dev/null
+++ b/www/statics/programs/Deal or no Deal_description.md
@@ -0,0 +1,5 @@
+A little game with the same principles as the same-named tv-show.
+The idea is that you have 26 cases with different amounts of money in it. You start by choosing your case, the money in it is now yours - but you don't know how much it is.
+
+Every round you open now a few of the other cases and narrow this way the money in your own down. And after ever round the "banker" offers you a price to buy your case.
+Its then your descision if you accept the deal or not. It's your descision how much you will risk to get as much money as possible.
\ No newline at end of file
diff --git a/www/statics/programs/Dynamic Link Fighters.php b/www/statics/programs/Dynamic Link Fighters.php
new file mode 100644
index 0000000..6612ca2
--- /dev/null
+++ b/www/statics/programs/Dynamic Link Fighters.php
@@ -0,0 +1,18 @@
+ 'Dynamic Link Fighters',
+ 'category' => 'Game',
+ 'stars' => 1,
+ 'ui_language' => 'English|German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Program your own KI and let it fight against others in a brutal deathmatch.',
+ 'add_date' => '2010-12-04',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Dynamic Link Fighters_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Dynamic Link Fighters.png',
+];
diff --git a/www/statics/programs/Dynamic Link Fighters_description.md b/www/statics/programs/Dynamic Link Fighters_description.md
new file mode 100644
index 0000000..c6c8156
--- /dev/null
+++ b/www/statics/programs/Dynamic Link Fighters_description.md
@@ -0,0 +1,6 @@
+And here is another fairly big project from me.
+A long time ago I had the idea of a program in which two computer programs play against each other. The two opponents get controlled by two dll's in which their KI is written.
+
+Now I finally have written this program, you can create your own KI in delphi (or theoretical in every language that can create dll's) and let it fight against others.
+
+For a detailed description how it works look at the included help-program.
\ No newline at end of file
diff --git a/www/statics/programs/ExtendedGitGraph.php b/www/statics/programs/ExtendedGitGraph.php
new file mode 100644
index 0000000..450f0ab
--- /dev/null
+++ b/www/statics/programs/ExtendedGitGraph.php
@@ -0,0 +1,18 @@
+ 'ExtendedGitGraph',
+ 'category' => 'Library',
+ 'stars' => 2,
+ 'ui_language' => 'English',
+ 'prog_language' => 'PHP',
+ 'short_description' => 'A simple php module to display a overview of you github commits',
+ 'add_date' => '2014-06-08',
+ 'urls' =>
+ [
+ 'download' => 'https://github.com/Mikescher/extendedGitGraph/',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/ExtendedGitGraph_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/ExtendedGitGraph.png',
+];
diff --git a/www/statics/programs/ExtendedGitGraph_description.md b/www/statics/programs/ExtendedGitGraph_description.md
new file mode 100644
index 0000000..46faf57
--- /dev/null
+++ b/www/statics/programs/ExtendedGitGraph_description.md
@@ -0,0 +1,3 @@
+A little PHP library to display and update an commit Overview from [Github](https://github.com/).
+
+Design-wise its similiar to the official Commit Graph from github - but you can see your commits over a bigger timeframe.
\ No newline at end of file
diff --git a/www/statics/programs/Graveyard of Numbers.php b/www/statics/programs/Graveyard of Numbers.php
new file mode 100644
index 0000000..6e4f9ca
--- /dev/null
+++ b/www/statics/programs/Graveyard of Numbers.php
@@ -0,0 +1,18 @@
+ 'Graveyard of Numbers',
+ 'category' => 'Tool',
+ 'stars' => 0,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'A little tool to continuously rename files.',
+ 'add_date' => '2008-10-01',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Graveyard of Numbers_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Graveyard of Numbers.png',
+];
diff --git a/www/statics/programs/Graveyard of Numbers_description.md b/www/statics/programs/Graveyard of Numbers_description.md
new file mode 100644
index 0000000..05c36e4
--- /dev/null
+++ b/www/statics/programs/Graveyard of Numbers_description.md
@@ -0,0 +1,5 @@
+A simple little tool to continuously rename files.
+
+It allows you to rename all files in a specific folder with a specified pattern and and ongoing number.
+
+It proves useful to batch rename a lot of files, for example images from a digital camera.
\ No newline at end of file
diff --git a/www/statics/programs/H2O.php b/www/statics/programs/H2O.php
new file mode 100644
index 0000000..6eea453
--- /dev/null
+++ b/www/statics/programs/H2O.php
@@ -0,0 +1,19 @@
+ 'H2O',
+ 'category' => 'Game',
+ 'stars' => 2,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Try creating the biggest chain reaction and see yourself climb up in the global l" +
+ "eaderboard.',
+ 'add_date' => '2009-01-24',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/H2O_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/H2O.png',
+];
diff --git a/www/statics/programs/H2O_description.md b/www/statics/programs/H2O_description.md
new file mode 100644
index 0000000..7f77dbb
--- /dev/null
+++ b/www/statics/programs/H2O_description.md
@@ -0,0 +1,6 @@
+H�O-Reaction is a little bigger project i did in the last few months.
+
+Your target is to create chain reaction in a grid of water-molecules, the bigger and longer this reaction is - the more points you will get.
+You can compare your personal highscore in an online leaderboard with already many players in it
+
+Just click on a molecule of your choice and watch the resulting reaction, have fun.
\ No newline at end of file
diff --git a/www/statics/programs/HexSolver.php b/www/statics/programs/HexSolver.php
new file mode 100644
index 0000000..4f93eab
--- /dev/null
+++ b/www/statics/programs/HexSolver.php
@@ -0,0 +1,19 @@
+ 'HexSolver',
+ 'category' => 'Tool',
+ 'stars' => 5,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C#',
+ 'short_description' => 'An automatic parser and solver for Hexcells, Hexcells Plus and Hexcells Infinite." +
+ "',
+ 'add_date' => '2015-05-06',
+ 'urls' =>
+ [
+ 'github' => 'https://github.com/Mikescher/HexSolver',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/HexSolver_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/HexSolver.png',
+];
diff --git a/www/statics/programs/HexSolver_description.md b/www/statics/programs/HexSolver_description.md
new file mode 100644
index 0000000..96e9dfe
--- /dev/null
+++ b/www/statics/programs/HexSolver_description.md
@@ -0,0 +1,34 @@
+An automatic solver for [Hexcells](http://www.matthewbrowngames.com/hexcells.html), [Hexcells Plus](http://www.matthewbrowngames.com/hexcellsplus.html) and [Hexcells Infinite](http://www.matthewbrowngames.com/hexcellsinfinite.html).
+The idea is to automatically parse the game state, find the next (valid) step and execute it.
+*(Rinse and Repeat until everything is solved)*
+
+### [> Animation](http://gfycat.com/GrotesqueRecklessAcornbarnacle)
+
+##Usage
+
+ - Start HexCells Infinite *(should also work with the other Hexcell games)*
+ - I recommend window-mode with 1440x900 resolution (for the OCR to work best)
+ - Load a level
+ - Start HexSolver
+ - Press **Recapture**
+ - If you want to completely solve the level press **Execute (All)**
+ - Don't manually move your mouse until finished (press ESC to abort)
+ - If you just want to see the next step press **Solve** (Can take around 5-10 seconds)
+
+##Troubleshooting
+
+ - HexSolver needs an minimum amount of orange cells to recognize the layout
+ - HexSolver only works when all cells are in an uniform grid (click **Calculate** to see the grid)
+ - Only click Recapture when the fading in effect is finished - otherwise no cells can be recognized
+ - If you find the (uncommon) case of two row-hint in one cell, HexSolver will fail *(sorry)*
+ - If HexSolver fails to solve a configuration or the OCR module fails, please send me an full-resolution screenshot of the game.
+
+##Features
+
+ - Automatic finding of game window and capturing of its graphical output
+ - Dynamically finding the hexagon layout
+ - With an custom crafted OCR module recognition of the cell values
+ - 3-Step solving of the current configuration (tested on the original levels and many of the generated ones)
+ - Finding the optimal execution path by solving the corresponding [TSP](http://en.wikipedia.org/wiki/Travelling_salesman_problem)
+ - Automatic execution by programmatically moving the mouse
+ - Saving the current (captured) state as an [*.hexcells](https://github.com/BlaXpirit/sixcells) file
diff --git a/www/statics/programs/Infinity Tournament.php b/www/statics/programs/Infinity Tournament.php
new file mode 100644
index 0000000..ac3e19d
--- /dev/null
+++ b/www/statics/programs/Infinity Tournament.php
@@ -0,0 +1,18 @@
+ 'Infinity Tournament',
+ 'category' => 'Game',
+ 'stars' => 4,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Java',
+ 'short_description' => 'A never ending Tower Defense where you fight against your own score.',
+ 'add_date' => '2012-04-14',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Infinity Tournament_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Infinity Tournament.png',
+];
diff --git a/www/statics/programs/Infinity Tournament_description.md b/www/statics/programs/Infinity Tournament_description.md
new file mode 100644
index 0000000..db1f043
--- /dev/null
+++ b/www/statics/programs/Infinity Tournament_description.md
@@ -0,0 +1,16 @@
+A while ago a friend and I developed a game for school. It was a Towerdefence game and i think it was pretty nice.
+The problem was that we developed it in Greenfoot - and we reached pretty fast the limitations of this framework.
+
+So after all that I decided to rewrite it completely new in my own game-framework [absCanvas](/programs/view/absCanvas).
+Infinity Tournament is a futuristic themed Towerdefence with an endless amount of waves that get hader with every round.
+
+It has some cool features like:
+
+- endless gameplay
+- online competitive highscore
+- multiple pre-made maps
+- a custom map-editor
+- futuristic-neon theme and free electro music
+- 3 different tower with multiple diferent upgrade stages
+
+Let's see how high *you* can get in the highscore
\ No newline at end of file
diff --git a/www/statics/programs/Keygen Dancer.php b/www/statics/programs/Keygen Dancer.php
new file mode 100644
index 0000000..e8352a5
--- /dev/null
+++ b/www/statics/programs/Keygen Dancer.php
@@ -0,0 +1,18 @@
+ 'Keygen Dancer',
+ 'category' => 'Gadget',
+ 'stars' => 2,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Delphi',
+ 'short_description' => '40 of the best keygen themes together with a funny little keygen dance animation." +
+ "',
+ 'add_date' => '2010-03-16',
+ 'urls' =>
+ [
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Keygen Dancer_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Keygen Dancer.png',
+];
diff --git a/www/statics/programs/Keygen Dancer_description.md b/www/statics/programs/Keygen Dancer_description.md
new file mode 100644
index 0000000..9c478d5
--- /dev/null
+++ b/www/statics/programs/Keygen Dancer_description.md
@@ -0,0 +1,46 @@
+You probably know that a lot of (old) Keygens had neat little animations and background music. There are even whole [sites](http://www.keygenmusic.net/) determined to collect these catchy tunes.
+
+Also a while ago I found in one of these programs (that I use only for the music...) a funny little dancing animation, and just for fun i extracted it.
+So now i thought i would combine them together to create this program that show a dancing character and plays a few Keygen sounds in the background.
+
+## Songs
+
+- AGAiN - FairStars
+- AGAiN - Moonflight
+- AGAiN - Smurf-Esque 98
+- AGAiN - Sunflower
+- AGAiN - Surrender
+- CORE - 1992
+- CORE - Adobe Premiere Elements 7
+- CORE - Bergsmätaren Lever
+- CORE - Dead Feelings
+- CORE - Mary's Monastery
+- CORE - Offencyt
+- CORE - Skogens Djur
+- Digital Insanity - Unreal Superhero
+- ECLiPSE - Battleship Chess
+- EDGE - Benny Hill
+- EDGE - Complications
+- EDGE - There Aren't Any Sheep in Outer Mongolia
+- FFF - Fighting for fun
+- FFF - Elrico vs. LHS
+- nGen - New Life
+- nGen - I'll fly with you
+- nGen - Its ram hot
+- nGen - nGen Racer Type Tune
+- ORiON - Keygen Tune
+- PARADOX - Alcatraz
+- PARADOX - Angels
+- PARADOX - Arkanoid
+- PARADOX - Auricorns Fishingboat
+- PARADOX - nVidia DVD Decoder 1.00.58
+- PARADOX - Scrambled Mind
+- Razor1911 - A message to you
+- Razor1911 - Battlefield 2142
+- Razor1911 - Cybernostra weekend
+- Razor1911 - Fuck da Police
+- Razor1911 - Gothic 3trn
+- Razor1911 - Kolobki Vodka Dance
+- Razor1911 - Mario Airlines
+- Razor1911 - My Dirty Old Camel
+- Razor1911 - NHL 07 auorun 1
\ No newline at end of file
diff --git a/www/statics/programs/LAN-Control.php b/www/statics/programs/LAN-Control.php
new file mode 100644
index 0000000..78ec61d
--- /dev/null
+++ b/www/statics/programs/LAN-Control.php
@@ -0,0 +1,18 @@
+ 'LAN-Control',
+ 'category' => 'Network administration',
+ 'stars' => 1,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Controll essential features of an other computer over the LAN',
+ 'add_date' => '2011-07-05',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/LAN-Control_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/LAN-Control.png',
+];
diff --git a/www/statics/programs/LAN-Control_description.md b/www/statics/programs/LAN-Control_description.md
new file mode 100644
index 0000000..7f91f18
--- /dev/null
+++ b/www/statics/programs/LAN-Control_description.md
@@ -0,0 +1,5 @@
+LAN Control is a tool to execute operations on another computer over a LAN connection.
+All you have to do is execute the `server.exe` on the remote computer and the `client.exe` on yours.
+After that you can do things like lock the PC, get executed programs, kill processes etc.
+
+I strongely advice to do this only one your own computer and not control other pc's. Except - you know - you have good reasons :).
\ No newline at end of file
diff --git a/www/statics/programs/LightShow.php b/www/statics/programs/LightShow.php
new file mode 100644
index 0000000..25f6736
--- /dev/null
+++ b/www/statics/programs/LightShow.php
@@ -0,0 +1,18 @@
+ 'LightShow',
+ 'category' => 'Hoax',
+ 'stars' => 0,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Turn you keyboard-LED\"s into a little lightshow',
+ 'add_date' => '2008-10-12',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/LightShow_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/LightShow.png',
+];
diff --git a/www/statics/programs/LightShow_description.md b/www/statics/programs/LightShow_description.md
new file mode 100644
index 0000000..e2e0dec
--- /dev/null
+++ b/www/statics/programs/LightShow_description.md
@@ -0,0 +1,2 @@
+LIghtShow generates literally a light show with the LED's on your keyboard. I'm not really sure if this has any practical use, but it looks kinda nice.
+Perhaps you could impress someone with the cool things your keybaord is able to do
\ No newline at end of file
diff --git a/www/statics/programs/Logistixx.php b/www/statics/programs/Logistixx.php
new file mode 100644
index 0000000..68a6208
--- /dev/null
+++ b/www/statics/programs/Logistixx.php
@@ -0,0 +1,18 @@
+ 'Logistixx',
+ 'category' => 'Mathematics',
+ 'stars' => 1,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Find the trick to escape the seemingly escape-proof maze.',
+ 'add_date' => '2008-12-20',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Logistixx_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Logistixx.png',
+];
diff --git a/www/statics/programs/Logistixx_description.md b/www/statics/programs/Logistixx_description.md
new file mode 100644
index 0000000..975460e
--- /dev/null
+++ b/www/statics/programs/Logistixx_description.md
@@ -0,0 +1,5 @@
+This is a little game made out of a funny little riddle.
+
+Your goal is to close very single door in a maze by walking through it and then escaping the maze.
+You can reset the level anytime with a big red reset button.
+I know the problem seems impossible, but i assure you that there is a valid trick to solve this.
\ No newline at end of file
diff --git a/www/statics/programs/NedSchend.php b/www/statics/programs/NedSchend.php
new file mode 100644
index 0000000..f699796
--- /dev/null
+++ b/www/statics/programs/NedSchend.php
@@ -0,0 +1,19 @@
+ 'NedSchend',
+ 'category' => 'Hoax',
+ 'stars' => 1,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Send anonymous messages over the Windows Messenger service to other pc\"s in your " +
+ "LAN',
+ 'add_date' => '2009-02-11',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/NedSchend_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/NedSchend.png',
+];
diff --git a/www/statics/programs/NedSchend_description.md b/www/statics/programs/NedSchend_description.md
new file mode 100644
index 0000000..465e5ae
--- /dev/null
+++ b/www/statics/programs/NedSchend_description.md
@@ -0,0 +1,7 @@
+If you ever where in a big LAN network with a little bit older computers (XP or older) you probably know the Windows Messenger Service.
+
+With the command netsend you are able to send messages directly onto the screen on another person. Unfortunately your computername will appear as sender, and everyone will know you send the message.
+
+If you know want to anonymously send messages you can use this little tool which lets you freely choose the displayed sendername, you can even choose the name of another computer and impersonate someone.
+
+I'm sure some of you are able to think about a few use cases for this tool ...
\ No newline at end of file
diff --git a/www/statics/programs/Passpad.php b/www/statics/programs/Passpad.php
new file mode 100644
index 0000000..75ad741
--- /dev/null
+++ b/www/statics/programs/Passpad.php
@@ -0,0 +1,19 @@
+ 'Passpad',
+ 'category' => 'Tool',
+ 'stars' => 3,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C#',
+ 'short_description' => 'A texteditor for encrypted textfiles (AES, Twofish, Blowfish, ...)',
+ 'add_date' => '2015-11-26',
+ 'urls' =>
+ [
+ 'download' => 'https://github.com/Mikescher/Passpad/releases',
+ 'github' => 'https://github.com/Mikescher/Passpad',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Passpad_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Passpad.png',
+];
diff --git a/www/statics/programs/Passpad_description.md b/www/statics/programs/Passpad_description.md
new file mode 100644
index 0000000..7949d1b
--- /dev/null
+++ b/www/statics/programs/Passpad_description.md
@@ -0,0 +1,20 @@
+A simple *(portable, single-executable)* editor for encrypted textfiles
+
+Supports:
+
+ - AES-256
+ - Blowfish
+ - Twofish
+ - CAST-128
+ - DES
+ - Triple DES
+
+
+
+The encrypted data is encoded as base-64 and saved in a simple text-file
+
+
+
+You can optionally specify a password hint for your encrypted files:
+
+
diff --git a/www/statics/programs/Serpilicum.php b/www/statics/programs/Serpilicum.php
new file mode 100644
index 0000000..786a112
--- /dev/null
+++ b/www/statics/programs/Serpilicum.php
@@ -0,0 +1,19 @@
+ 'Serpilicum',
+ 'category' => 'Game',
+ 'stars' => 3,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C++',
+ 'short_description' => 'A crazy little Snake with an \"Console\" Style',
+ 'add_date' => '2013-07-08',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ 'github' => 'https://github.com/Mikescher/Serpilicum',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Serpilicum_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Serpilicum.png',
+];
diff --git a/www/statics/programs/Serpilicum_description.md b/www/statics/programs/Serpilicum_description.md
new file mode 100644
index 0000000..e33b348
--- /dev/null
+++ b/www/statics/programs/Serpilicum_description.md
@@ -0,0 +1,5 @@
+A little Snake that [Armin Benz](http://sam-dev.de/) and I programmed in our second informatik semester.
+Even though it looks like a console application, it is - in fact - an OpenGL window. You will notice this later when a few effects start to kick in :)
+
+There is a local Highscore and multiple gamemodes.
+Be aware that this was our first real C++ project, and so there *might* be many bugs, and the sourcecode looks **really** horrible ...
\ No newline at end of file
diff --git a/www/statics/programs/SharkSim.php b/www/statics/programs/SharkSim.php
new file mode 100644
index 0000000..ca4b9ca
--- /dev/null
+++ b/www/statics/programs/SharkSim.php
@@ -0,0 +1,17 @@
+ 'SharkSim',
+ 'category' => 'Simulation',
+ 'stars' => 3,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C++',
+ 'short_description' => 'A simple implementation of the Wa-Tor cellular automaton',
+ 'add_date' => '2013-07-12',
+ 'urls' =>
+ [
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/SharkSim_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/SharkSim.png',
+];
diff --git a/www/statics/programs/SharkSim_description.md b/www/statics/programs/SharkSim_description.md
new file mode 100644
index 0000000..b11e1c1
--- /dev/null
+++ b/www/statics/programs/SharkSim_description.md
@@ -0,0 +1,14 @@
+SharkSim is my take on a Wa-Tor simulation ([wikipedia.org/wiki/Wator](wikipedia.org/wiki/Wator))
+
+The rules of this [cellular automaton](http://en.wikipedia.org/wiki/Cellular_automaton) are:
+
+> Time passes in discrete jumps, which I shall call chronons.
+> During each chronon a fish or shark may move north, east, south or west to an adjacent point, provided the point is not already occupied by a member of its own species.
+> A random-number generator makes the actual choice.
+> For a fish the choice is simple: select one unoccupied adjacent point at random and move there.
+> If all four adjacent points are occupied, the fish does not move.
+> Since hunting for fish takes priority over mere movement, the rules for a shark are more complicated:
+> from the adjacent points occupied by fish, select one at random, move there and devour the fish.
+> If no fish are in the neighborhood, the shark moves just as a fish does, avoiding its fellow sharks.
+
+My implementation is not that fancy - but it gets to a stable FPS rate of 45 with a map of the size 600x600.
diff --git a/www/statics/programs/Sieb des Eratosthenes.php b/www/statics/programs/Sieb des Eratosthenes.php
new file mode 100644
index 0000000..d5900d7
--- /dev/null
+++ b/www/statics/programs/Sieb des Eratosthenes.php
@@ -0,0 +1,18 @@
+ 'Sieb des Eratosthenes',
+ 'category' => 'Mathematics',
+ 'stars' => 1,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Visualize the prime number calculation with the Sieve of Erastothenes algorithm.',
+ 'add_date' => '2009-01-22',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Sieb des Eratosthenes_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Sieb des Eratosthenes.png',
+];
diff --git a/www/statics/programs/Sieb des Eratosthenes_description.md b/www/statics/programs/Sieb des Eratosthenes_description.md
new file mode 100644
index 0000000..4c39fbf
--- /dev/null
+++ b/www/statics/programs/Sieb des Eratosthenes_description.md
@@ -0,0 +1,3 @@
+The [Sive of Ersathothenes](http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes) algorithm is a good way to get all prime numbers up to a specific limit.
+
+This programm visualized the algorithm in an *hopefully* easy-to-understand way.
\ No newline at end of file
diff --git a/www/statics/programs/Smart Directory Lister.php b/www/statics/programs/Smart Directory Lister.php
new file mode 100644
index 0000000..44da82c
--- /dev/null
+++ b/www/statics/programs/Smart Directory Lister.php
@@ -0,0 +1,19 @@
+ 'Smart Directory Lister',
+ 'category' => 'Tool',
+ 'stars' => 2,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'List all files in a folder that match a specific pattern and export them in plain" +
+ "text.',
+ 'add_date' => '2010-01-12',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Smart Directory Lister_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Smart Directory Lister.png',
+];
diff --git a/www/statics/programs/Smart Directory Lister_description.md b/www/statics/programs/Smart Directory Lister_description.md
new file mode 100644
index 0000000..369a720
--- /dev/null
+++ b/www/statics/programs/Smart Directory Lister_description.md
@@ -0,0 +1,3 @@
+With Smart Directory Lister (*short* SDL) you can easily list all files or folder in a folder that match a pattern. After that you can export that list as plain text.
+
+As simple as that sounds its really useful to create a list of all your programs/movies/photos etc. Also because this programm creates no files and is pretty small you can just copy the executable into every folder you need to create a list f sometimes.
\ No newline at end of file
diff --git a/www/statics/programs/SuperBitBros.php b/www/statics/programs/SuperBitBros.php
new file mode 100644
index 0000000..9eb9e8d
--- /dev/null
+++ b/www/statics/programs/SuperBitBros.php
@@ -0,0 +1,19 @@
+ 'SuperBitBros',
+ 'category' => 'Game',
+ 'stars' => 4,
+ 'ui_language' => 'English',
+ 'prog_language' => 'C#',
+ 'short_description' => 'A clone of all original SuperMarioBros (NES) levels, with a few tweaks.',
+ 'add_date' => '2013-10-17',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ 'github' => 'https://github.com/Mikescher/SuperBitBros',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/SuperBitBros_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/SuperBitBros.png',
+];
diff --git a/www/statics/programs/SuperBitBros_description.md b/www/statics/programs/SuperBitBros_description.md
new file mode 100644
index 0000000..6841d84
--- /dev/null
+++ b/www/statics/programs/SuperBitBros_description.md
@@ -0,0 +1,9 @@
+SuperBitBros is a clone of the original Super Mario for the NES.
+I took the time and converted all of the original levels into my own level format that I use for SuperBitBros. So you can play all the old levels with a little tweak:
+When you die, and you have no lifes left, you have to start over.
+So you could argue that this is essentially a rogue-like Super-Mario. Most of the things remained unchanged but I tweaked the amount of coins you get so its not totally impossible to beat the whole game.
+Also I added 3 different skins, mainly because I'm totally untalented with graphics and my first two attempts didn't pleased me :).
+
+If you want you can create your own levels, every level is just a simple .ora image - there currently no way to load custom levels, but it should be fairly easy to recompile the program.
+
+Have fun
\ No newline at end of file
diff --git a/www/statics/programs/TicTacToe.php b/www/statics/programs/TicTacToe.php
new file mode 100644
index 0000000..7bda73b
--- /dev/null
+++ b/www/statics/programs/TicTacToe.php
@@ -0,0 +1,18 @@
+ 'TicTacToe',
+ 'category' => 'Game',
+ 'stars' => 1,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'The classical Tic-Tac-Toe, complete with perfect KI and Sourcecode.',
+ 'add_date' => '2011-01-19',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/TicTacToe_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/TicTacToe.png',
+];
diff --git a/www/statics/programs/TicTacToe_description.md b/www/statics/programs/TicTacToe_description.md
new file mode 100644
index 0000000..39079fe
--- /dev/null
+++ b/www/statics/programs/TicTacToe_description.md
@@ -0,0 +1,4 @@
+This is a really basic TicTacToe game. You can play against a friend or against a computer enemy.
+The computer is intelligent enough to never loose, so all you can do is force a tie against him.
+
+Because the sourcecode was that short it is directly included - perhaps someone is interested in the KI (MinMax algorithm)
\ No newline at end of file
diff --git a/www/statics/programs/Ziegenproblem.php b/www/statics/programs/Ziegenproblem.php
new file mode 100644
index 0000000..08c0c88
--- /dev/null
+++ b/www/statics/programs/Ziegenproblem.php
@@ -0,0 +1,19 @@
+ 'Ziegenproblem',
+ 'category' => 'Mathematics',
+ 'stars' => 0,
+ 'ui_language' => 'German',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'Simulate the popular Monty Hall problem (ger: Ziegenproblem) with this program fo" +
+ "r yourself.',
+ 'add_date' => '2008-04-10',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/Ziegenproblem_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/Ziegenproblem.png',
+];
diff --git a/www/statics/programs/Ziegenproblem_description.md b/www/statics/programs/Ziegenproblem_description.md
new file mode 100644
index 0000000..8e79dcf
--- /dev/null
+++ b/www/statics/programs/Ziegenproblem_description.md
@@ -0,0 +1,7 @@
+The [Monty-Hall-Problem](http://en.wikipedia.org/wiki/Monty_Hall_problem) is an old mathematical riddle
+
+> Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?
+
+The answer - even though it might seem strange - is **yes**, you should change.
+For the full mathematical proof you can read wikipedia, but to visualize the problem you can use this little program and test it by yourself.
+You can even automate a few hundred tests and see whats right on average.
\ No newline at end of file
diff --git a/www/statics/programs/absCanvas.php b/www/statics/programs/absCanvas.php
new file mode 100644
index 0000000..b3097fa
--- /dev/null
+++ b/www/statics/programs/absCanvas.php
@@ -0,0 +1,19 @@
+ 'absCanvas',
+ 'category' => 'Engine',
+ 'stars' => 3,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Java',
+ 'short_description' => 'A powerful 2D Tiled-Game-Engine for java. Completely in canvas and with network s" +
+ "upport.',
+ 'add_date' => '2012-05-28',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/absCanvas_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/absCanvas.png',
+];
diff --git a/www/statics/programs/absCanvas_description.md b/www/statics/programs/absCanvas_description.md
new file mode 100644
index 0000000..d91a5ff
--- /dev/null
+++ b/www/statics/programs/absCanvas_description.md
@@ -0,0 +1,16 @@
+absCanvas is my very own java game engine. And by the time it is probably the project i used in the most other things.
+
+The idea was to create a (in the beginning) very simple game engine that doesn't depend on other libraries.
+*(except a few, like a sound library - if you use sounds)*
+The drawing is down per Active-Rendering directly on the normal canvas.
+
+The main advantage are the multiple integrated features like
+
+- a complex menusystem with different components, different screens and even animated transitions between them.
+- classes to support loading sprites from spritesheets and to create animated entities.
+- configurable collision detection
+- a *(not fully finished)* Network support where multiple people control different entities on the same world.
+- my own custom map saveformat with IO classes and an editor
+
+absCanvas was initially only for my own projects, and if you want to write a game you are probably better to just use one of the bigger game frameworks.
+But if you want to see a game framework, made completely from the bottom of java this could be interesting
\ No newline at end of file
diff --git a/www/statics/programs/exeExtract.php b/www/statics/programs/exeExtract.php
new file mode 100644
index 0000000..b2cadc5
--- /dev/null
+++ b/www/statics/programs/exeExtract.php
@@ -0,0 +1,18 @@
+ 'exeExtract',
+ 'category' => 'Tool',
+ 'stars' => 0,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Delphi',
+ 'short_description' => 'A simple tool to copy all files of a specific extension from a folder.',
+ 'add_date' => '2008-03-26',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/exeExtract_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/exeExtract.png',
+];
diff --git a/www/statics/programs/exeExtract_description.md b/www/statics/programs/exeExtract_description.md
new file mode 100644
index 0000000..4eb7cb1
--- /dev/null
+++ b/www/statics/programs/exeExtract_description.md
@@ -0,0 +1,5 @@
+exeExtract is a little tool to extract many files from a given folder.
+
+It proved especially useful to me when i needed to get every compiled exe file from all of my project folders.
+
+But - even the name hints otherwise - you can freely choose what pattern what the to copy files have to match.
\ No newline at end of file
diff --git a/www/statics/programs/jCircuits.php b/www/statics/programs/jCircuits.php
new file mode 100644
index 0000000..64c1979
--- /dev/null
+++ b/www/statics/programs/jCircuits.php
@@ -0,0 +1,19 @@
+ 'jCircuits',
+ 'category' => 'Simulation',
+ 'stars' => 4,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Java',
+ 'short_description' => 'A fully featured logical circuit simulator with many prebuild components',
+ 'add_date' => '2011-12-16',
+ 'urls' =>
+ [
+ 'download' => 'direkt',
+ 'sourceforge' => 'http://sourceforge.net/projects/jcircuits/',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/jCircuits_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/jCircuits.png',
+];
diff --git a/www/statics/programs/jCircuits_description.md b/www/statics/programs/jCircuits_description.md
new file mode 100644
index 0000000..8bb2700
--- /dev/null
+++ b/www/statics/programs/jCircuits_description.md
@@ -0,0 +1,64 @@
+jCircuits is a logic circuits simulation.
+
+It allows you to create and wire your own circuits and then observe how they behave.
+Beside all basic gatters there are also more advanced elements and a few premade examples.
+
+A special feature is the 3D mode, to see your circuit layout on a 3D surface.
+And the simplistic graphic for each component.
+
+###Components
+
+####Basic
+
+- Source (Simple Lever)
+- Target (Display)
+- NOT
+- AND
+- NAND
+- OR
+- NOR
+- XOR
+- XNOR
+
+####Advanced
+
+- Half Adder
+- Full Adder
+- JK-FlipFlop
+- D-FlipFlop
+- Multiplexer
+- Demultiplexer
+
+####Bus
+
+- Bus-Bin-Source (8Bit Binary Chooser)
+- Bus-Bin-Target (8Bit Binary Display)
+- Bus-Dec-Source (8Bit Decimal Chooser)
+- Bus-Dec-Target (8Bit Decimal Display)
+- Bus-Hex-Source (8Bit Hex Chooser)
+- Bus-Hex-Target (8Bit Hex Display)
+- Bus-Splitter
+- Bus-Merger
+- Bus: NOT
+- Bus: ADD-1
+- Bus: SUB-1
+- Bus: SHIFT-LEFT
+- Bus: SHIFT-RIGHT
+- Bus: ADD
+- Bus: SUB
+- Bus: MULT
+- Bus: DIV
+- Bus: AND
+- Bus: NAND
+- Bus: OR
+- Bus: NOR
+- Bus: XOR
+- Bus: XNOR
+
+#####Premade Circuits
+
+- XOR-Adder
+- Half-Adder
+- Full-Adder
+- Data-FlipFlop
+- Multiplexer
\ No newline at end of file
diff --git a/www/statics/programs/jClipCorn.php b/www/statics/programs/jClipCorn.php
new file mode 100644
index 0000000..e098888
--- /dev/null
+++ b/www/statics/programs/jClipCorn.php
@@ -0,0 +1,20 @@
+ 'jClipCorn',
+ 'category' => 'Tool',
+ 'stars' => 4,
+ 'ui_language' => 'English|German',
+ 'prog_language' => 'Java',
+ 'short_description' => 'Organize your movies and series on an external hard drive.',
+ 'add_date' => '2012-10-28',
+ 'urls' =>
+ [
+ 'download' => 'https://github.com/Mikescher/jClipCorn/releases',
+ 'github' => 'https://github.com/Mikescher/jClipCorn/',
+ 'wiki' => 'https://github.com/Mikescher/jClipCorn/wiki',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/jClipCorn_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/jClipCorn.png',
+];
diff --git a/www/statics/programs/jClipCorn_description.md b/www/statics/programs/jClipCorn_description.md
new file mode 100644
index 0000000..96a054e
--- /dev/null
+++ b/www/statics/programs/jClipCorn_description.md
@@ -0,0 +1,93 @@
+jClipCorn
+------------------
+*a portable movie and series manager for Windows and Linux*
+
+
+
+> **Disclaimer:**
+> Use this software only in a country which allows for private copies of your bought DVD's.
+> Use this software only to manage copies of movies which you own.
+
+
+
+### Main Features
+
+ - Fully portable - leave the program, the database and the settings on the same *(external)* drive as your movies
+ - Multi language (German & English), if you want you can help me translate it into other languages.
+ - Parse meta data from the [IMDB](http://www.imdb.com/)
+ - Filter your movies by many different criterias (date, genre, name, film series, quality, language, MPAA rating ...)
+ - Remember which movies you have watched and where you are in a series
+ - Automatically generate nice file names and folder structures for your movies and series
+ - Generate statistics from your ClipCorn database
+ - Tag and rate your watched movies
+ - Works under Windows, Linux *(and probably OS X)*
+
+#[> DOWNLOAD](http://www.github.com/Mikescher/jClipCorn/releases)
+###[> HOMEPAGE](http://www.mikescher.com/programs/view/jClipCorn)
+###[> GITHUB WIKI](https://github.com/Mikescher/jClipCorn/wiki)
+###[> CHANGELOG](https://raw.githubusercontent.com/Mikescher/jClipCorn/master/changelog.txt)
+
+### Organization
+
+The idea of ClipCorn is to have all movies in a single folder together with the ClipCorn executable and its database on an external hard drive.
+You can use it in a different way, but for the best user experience it's recommended to follow the organization guide for which this tool was developed.
+
+Every movie is named by a specific pattern. After you have added movies to your database you can rename the files to this pattern with the *"Check Database"* menu entry.
+The movies are afterwards named like this:
+
+~~~
+Stirb Langsam IV (Part 2).avi
+Spongebob - Lost in Time.mpg
+Terminator II - Tag der Abrechnung (Part 1).avi
+X-Men I.avi
+X-Men Origins - Wolverine.avi
+X-Men III.avi
+Shadowless Sword (Part1).avi
+Forrest Gump [Eng].mpg
+Terminator II - Tag der Abrechnung [Ger] (Part 1).avi
+~~~
+*(the exact rules, encoded as an [EBNF](https://en.wikipedia.org/wiki/Extended_Backus%E2%80%93Naur_Form) can be found under the help menu)*
+
+Series have an unique folder per series (with the series name), after that a folder for each season and then files with the file name pattern `SxxExx - %name%`. For example: `S01E07 - You Win or You Die.avi`
+You can create the folder structure for series by right clicking on a series and selecting *"Create folder structure"*
+
+Because series tend to become quite large you can also put them on their own external drive.
+A special [format syntax](https://github.com/Mikescher/jClipCorn/wiki/Relative-paths) guarantees that the paths to these series stay valid.
+
+### First start
+
+First copy the executable (either jClipCorn.jar or jClipCorn.exe) into the folder where you have your movies, then execute it (it needs read and write permissions).
+
+On the first start it should create a folder "*ClipCornDB*" where the database is stored.
+
+
+
+You can see this in the log view (icon in the bottom status bar, to the right of the progress bar).
+
+
+
+At first you should look into the settings and eventually change a few things, important are:
+
+ - UI Language
+ - Look'n'Feel (It's recommended to either use *Windows* or *Metal*)
+ - VLC Path (path to *vlc.exe*, for playing. You can also use another player - but it works best with the [VLC player](http://www.videolan.org/vlc/))
+ - The backup settings (I recommend to **enable** automatic backups *(like every 7 days or so)*)
+ - Automatic relative paths (this should really stay active - otherwise paths will be absolute and everything can go havoc if ClipCorn runs on an external drive)
+
+After that you can start adding your movies and series.
+
+### Adding a movie
+
+####[(go to wiki)](https://github.com/Mikescher/jClipCorn/wiki/Add-new-movie)
+
+### User Interface
+
+####[(go to wiki)](https://github.com/Mikescher/jClipCorn/wiki/User-Interface)
+
+### Adding a series
+
+####[(go to wiki)](https://github.com/Mikescher/jClipCorn/wiki/Add-new-series)
+
+### Check Database for errors
+
+####[(go to wiki)](https://github.com/Mikescher/jClipCorn/wiki/Check-database)
\ No newline at end of file
diff --git a/www/statics/programs/jQCCounter.php b/www/statics/programs/jQCCounter.php
new file mode 100644
index 0000000..9ed2ca8
--- /dev/null
+++ b/www/statics/programs/jQCCounter.php
@@ -0,0 +1,18 @@
+ 'jQCCounter',
+ 'category' => 'Tool',
+ 'stars' => 3,
+ 'ui_language' => 'English',
+ 'prog_language' => 'Java',
+ 'short_description' => 'A little tool to find the \"line of codes\" of multiple projects',
+ 'add_date' => '2014-04-27',
+ 'urls' =>
+ [
+ 'github' => 'https://github.com/Mikescher/jQCCounter',
+ ],
+ 'long_description' => function(){ return file_get_contents(__DIR__ . '/jQCCounter_description.md'); },
+ 'thumbnail_url' => '/images/program_thumbnails/jQCCounter.png',
+];
diff --git a/www/statics/programs/jQCCounter_description.md b/www/statics/programs/jQCCounter_description.md
new file mode 100644
index 0000000..32a4ed6
--- /dev/null
+++ b/www/statics/programs/jQCCounter_description.md
@@ -0,0 +1,4 @@
+This is a little handy tool - mainly for my own personal use.
+
+It scans a folder for (programming) projects and counts the total amount of sourcecode lines.
+It also scans for todo-comments (or every other thing you can express with regex)
\ No newline at end of file